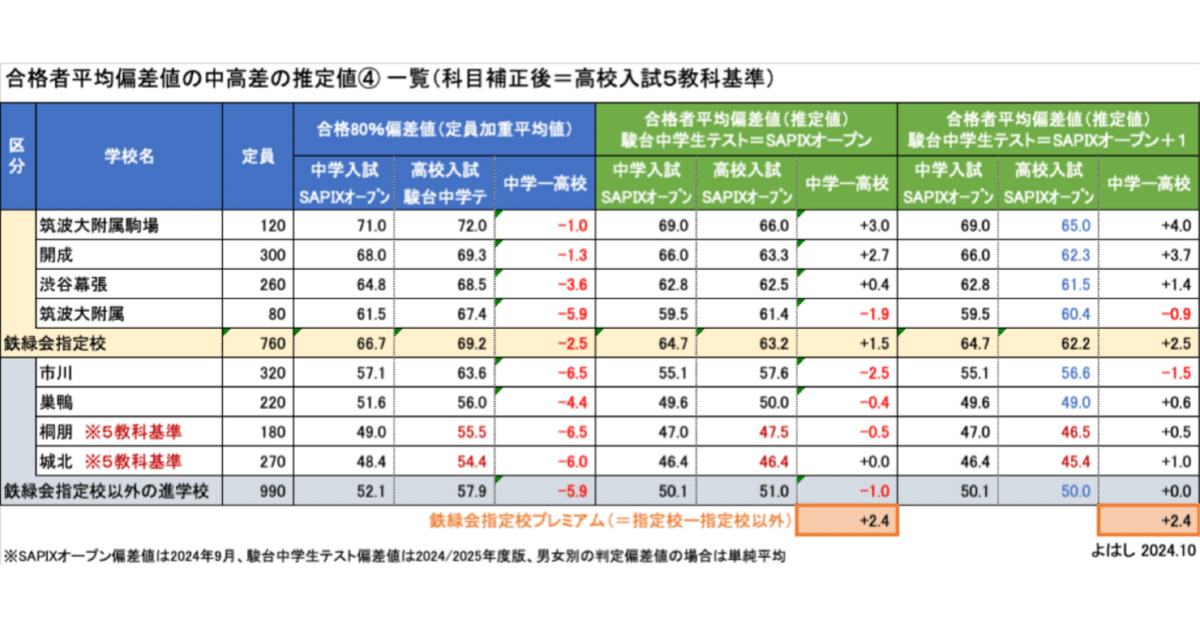
鉄緑会指定校プレミアムはSAPIX偏差値で+2〜3に相当する。
※以下の内容は鉄緑会が提供している情報を一切使用せずに、鉄緑会以外の情報源から推定した結果となります
Xにこちらのブログの紹介がポストされていました。高校募集している一貫校のSAPIX偏差値(中学受験)と駿台偏差値(高校受験)の比較記事です。
こちらの記事を読んだ際に、「鉄緑会の指定校と指定校以外を比較したら、鉄緑会プレミアムを算定できるのではないか!?」と思いつきました。そこで、今回は「鉄緑会プレミアム」の推定をやってみます。
なお、上記のブログにも明記されていますが、中学受験のSAPIXオープン偏差値と高校受験の駿台中学生テスト偏差値は母集団が違うため、単純比較はできません。これについては、私のこちらの考察に基づいて同等の学力レベルの標本を用いた変換モデルを導入して、やや強引に比較します。当然、誤差はありますので、あくまで一つの参考値として見てください。
0. まとめ
鉄緑会プレミアム=(指定校の合格者平均偏差値の中学受験と高校受験の差)ー(指定校以外の進学校の合格者平均偏差値の中学受験と高校受験の差)と定義する。
この場合、「駿台中学テスト偏差値≒SAPIXオープン偏差値+α(αは0〜1)」という変換モデルの下では、αの数字に関わらず、鉄緑会プレミアムは+2.4(科目補正あり)、+3.3(科目補正なし)となる。
このことから、鉄緑会プレミアム=中学受験で鉄緑会指定校に入学して中1で鉄緑会に入学できる権利の価値は、SAPIXオープン偏差値の+2〜3に相当すると言える。
1. 鉄緑会指定校の分析
鉄緑会指定校(2024年10月時点)のうち、高校受験も行っているのは、私立では開成中と渋谷幕張中、国立では筑波大附属駒場中と筑波大附属中の合計4校です。これらについて、中学受験のSAPIXオープン偏差値、高校受験の駿台中学生テスト偏差値を整理すると、この表のようになります。
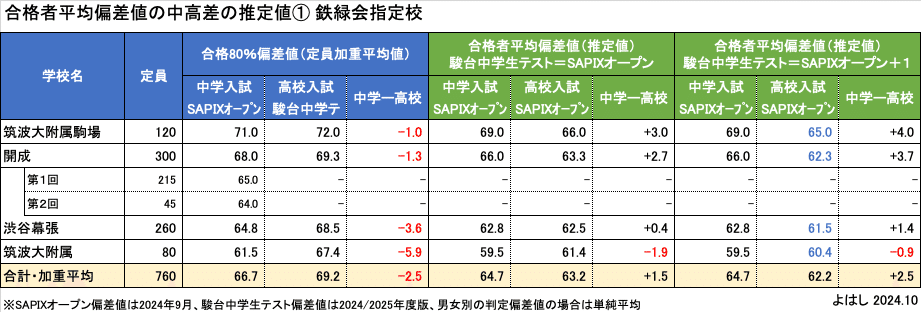
まず、左のブルーの列が合格可能性80%の偏差値をそのまま記載したものです。SAPIXオープンの方が低い数字となっており、中学ー高校の差はマイナスとなっています。
この2つは母集団も判定基準も違うため、単純比較できません。この2つの模試を比較するために、合格者平均偏差値に換算して、母集団のレベル調整を行っているのがグリーンの列です。グリーンはあくまで推定値となります。
合格者平均偏差値への換算は、これまでの分析に基づいて、SAPIXオープンでは合格者平均偏差値=合格80%偏差値ー2、駿台中学生テストでは合格者平均偏差値=合格80%偏差値ー6で計算しています。その上で、2つの模試の変換式は「駿台中学生テスト偏差値=SAPIXオープン偏差値+α(αは0〜1)」を採用しています。
グリーンの真ん中のブロックがα=0で「駿台中学生テスト偏差値=SAPIXオープン偏差値」となる場合です。SAPIXオープン偏差値を基準に高校入試側を変換していますが、α=0なのでどちらも元の合格者平均偏差値の推定値と同じ値です。
このケースでは、合格者平均偏差値の中学と高校の差は、筑波大附属駒場と開成で大きくプラス(+3.0と+2.7)、渋谷幕張はほぼゼロ(+0.4)、筑波大附属はマイナス(-1.9)となりました。指定校4校の加重平均の中学と高校の差は+1.5です。
一方、α=1としたのが、グリーンの右のブロックです。変換式は「駿台中学生テスト偏差値=SAPIXオープン偏差値+1」となり、SAPIXオープン偏差値を基準に高校入試側を変換するので、高校入試はそれぞれマイナス1されています。このケースでは、全ての差が+1されるので、指定校4校の加重平均の中学と高校の差は+2.5となります。
では、この+1.5や+2.5が鉄緑会プレミアムなのでしょうか? そうではありません。これは中学入試と高校入試の差であり、この段階で言えることは「鉄緑会指定校の4校では、平均的には、中学入学組の方が高校入学組よりも、入学時点の学力レベルがやや高い(SAPIX偏差値で+1.5〜2.5に相当)」ということまでです。
※あくまでも入学時点での分析であり、中学入学組の6年後、高校入学組の3年後の卒業時の学力=大学合格実績の差ではありません。
この入学時点での学力レベルの差(+1.5〜2.5)には鉄緑会プレミアムも含まれますが、他の要因も含まれています。鉄緑会のプレミアムは指定校と指定校以外の差なので、同じ分析を指定校以外でも行って、算定する必要があります。そこで、次は指定校以外を見てみます。
2. 鉄緑会指定校以外の進学校の分析
首都圏の中高一貫校のうち、東大に一定数(二桁)が合格する学校で、高校募集も行っているのは、私立では市川中・巣鴨中・桐朋中・城北中、国立では学芸大附属の各中学となります。このうち学芸大附属は内部進学テストの影響で中学受験の難易度と高校受験の難易度が大きく違うようなので、今回の分析対象から除外して、私立の4校を対象に分析します。
鉄緑会指定校と同じ計算を、この4校に対して行った結果がこちらになります。

グリーンの合格者平均偏差値の母集団調整を行った部分を見ると、ほぼ全ての学校で中学と高校の差がマイナスになっています。加重平均では、駿台中学生テスト=SAPIXオープン+αの変換において、合格者平均偏差値の中学と高校の差は-1.9(α=0)、-0.9(α=1)となりました。
ここまでの分析から、「鉄緑会指定校以外の進学校の4校では、中学受験4教科・高校受験3教科の基準において、平均的には、中学入学組の方が高校入学組よりも、入学時点の学力レベルがやや低い(-1.9〜0.9)」ということが言えます。こちらも、中学入学組の6年後、高校入学組の3年後の卒業時の学力=大学合格実績の差ではありません。
※後述しますが、5教科基準にするとこの差は-1.0〜0.0に圧縮され、中学入学組と高校入学組の学力レベルはほぼ同等とも考えられます。
3. 鉄緑会プレミアムの算定
上記の分析で、鉄緑会指定校4校と指定校以外の進学校4校のデータが集まりました。一覧にするとこのようになります。
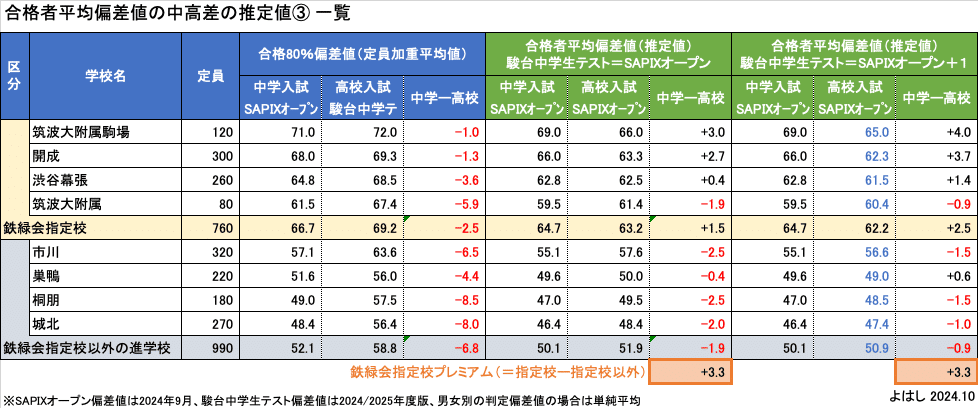
ここで改めて、鉄緑会プレミアム=(指定校の合格者平均偏差値の中学受験と高校受験の差)ー(指定校以外の進学校の合格者平均偏差値の中学受験と高校受験の差)と定義します。
この計算を上記の表3で行うと、グリーン中央(α=0のケース)では鉄緑会プレミアム=(+1.5)ー(-1.9)=+3.3となります。グリーン右(α=1のケース)でも同様に、鉄緑会プレミアム=+3.3です。
中学受験と高校受験の鉄緑会プレミアム以外の差は、指定校でも指定校以外でも同様に存在するため、上記の右辺で相殺されます。また、SAPIXオープンと駿台中学生テストの変換式の加算分(α)も、指定校でも指定校以外でも同じ値で調整されるため、右辺で相殺されます。つまり、鉄緑会指定校プレミアムは、中学受験と高校受験の差、模試の変換式に依存しないことになります。
ただし、この時に注意すべきことが1点あります。鉄緑会指定校の4校は高校受験は全ての学校が5教科入試ですが、指定校以外では、市川・巣鴨は5教科入試、桐朋・城北は3教科入試です。一般論として、入試の科目数が下がるほど、持ち偏差値は上がり、合格者平均偏差値も上がります。8校の比較の基準を合わせるには、この補正が必要になります。
そこで、過去の分析に基づいて、科目数が1減るのに対して合格者平均偏差値をマイナス1する補正を行い、高校入試を5教科基準に合わせたのがこちらの表です。この場合、鉄緑会プレミアム=+2.4となりました。
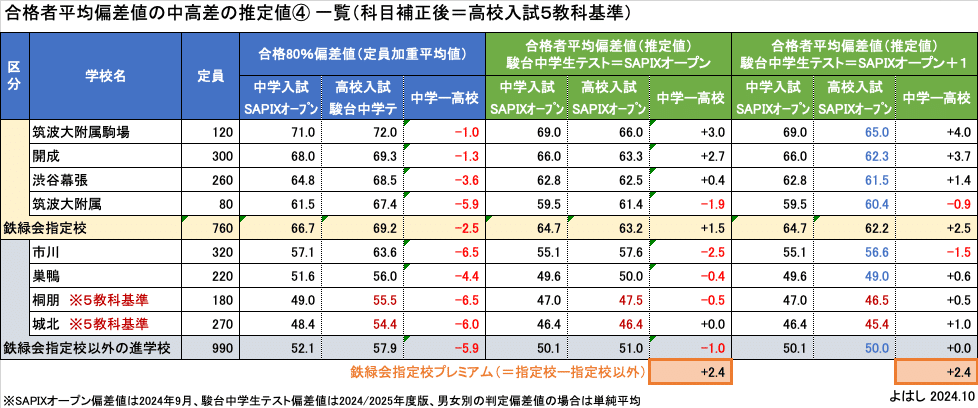
4. 附属校プレミアムとの違い
上記から鉄緑会指定校プレミアムはSAPIXオープン偏差値で+2〜3となりますが、これは過去に算定した附属校プレミアムとは種類が異なります。附属校プレミアムは大学附属校に発生する入学時期の差であり、鉄緑会指定校プレミアムは進学校の中で鉄緑会指定校と指定校以外の差です。一覧にして整理すると、このようになります。
①附属校プレミアム=大学入学権利を附属校で獲得する価値=附属校の中学入試の合格者平均偏差値ー大学入試合格者平均偏差値
早慶附属校:中学ー大学=+2.2 →附属校プレミアムあり
MARCH附属校:中学ー大学=+0.2 →附属校プレミアムなし
②鉄緑会指定校プレミアム=鉄緑会入塾の権利を獲得する価値=中学入学と高校入学の合格者平均偏差値の違いについての指定校と指定校以外の差
指定校の進学校:中学ー高校=+1.5〜2.5
指定校以外の進学校:中学ー高校=-1.0〜0.0 ※5科目基準
指定校と指定校以外の差=(+1.5〜2.5)ー(-1.0〜0.0)=+2.4 →鉄緑会指定校プレミアム
5. 最後に
今回の分析の結果、「高校募集も行っている中高一貫進学校における鉄緑会指定校プレミアムはSAPIXオープン偏差値で+2〜3」と推定されました。
ただし、これは鉄緑会指定校になるとSAPIXオープンの合格可能性偏差値が+2〜3になるという因果関係を意味しているものではありません。中学受験と高校受験の合格者平均値の差が、指定校の方が+2〜3高いという結果説明です。ただ、逆に考えると、結果として指定校と指定校以外で出る差分のうちいくらかは、中学受験で鉄緑会指定校に入学して、そのまま中1で鉄緑会に入学できる権利の価値を意味するとも考えられます。そして、この権利の価値が差分100%と仮定すると、その数字が鉄緑会指定校プレミアムとなります。
ここまでの分析で、鉄緑会指定校プレミアムは推定できました。では、指定校で中1から鉄緑会に入塾するのではなく、入塾テストに合格して鉄緑会に入塾する難易度はどの程度になるのでしょうか? 次回はこの分析をやってみたいと思います。
この記事が気に入ったらサポートをしてみませんか?
