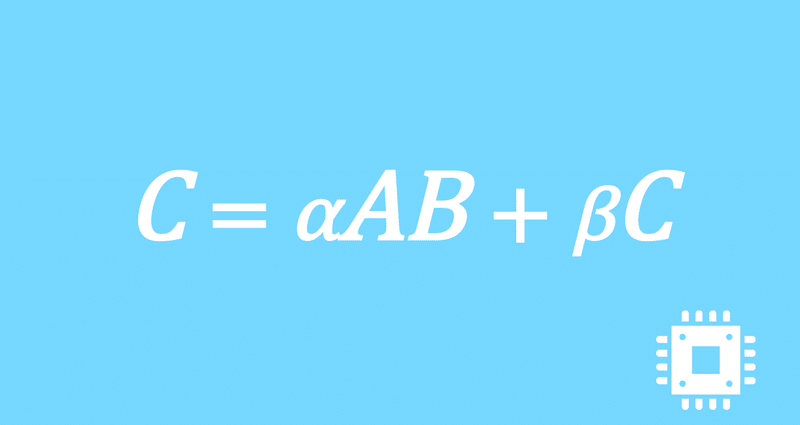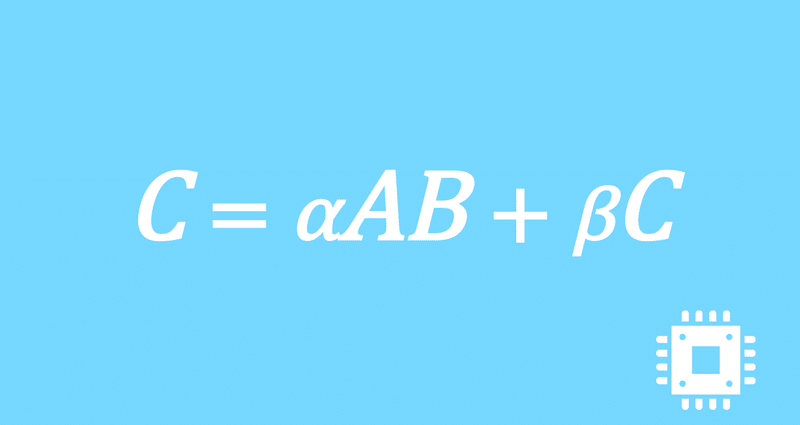マガジンのカバー画像

行列積計算を高速化してみた

30
本
数値計算ライブラリBLASに含まれる行列積ルーチンDGEMMを高速化していく手順を記した記事「行列積計算を高速化してみる」の章ごとに分割した記事をまとめたマガジンです。元の記事は…
運営しているクリエイター
やまもと
固定された記事

はじめに｜行列積高速化#0

以前書いた行列計算DGEMMを高速化する記事が、あまりに長すぎた（20万文字以上）ので、記事あたり１万字以内を目安に、章ごとに記事を分割することにしました。 元の記事が有料記事のため、高速化の重要なカギになる章は有料にさせていただいています。全記事をご購入いただくと1000円になります。元の記事は560円ですので、全ての章を読むなら元の記事の方が割安になっています。一部の章は元の記事で有料部分に含まれていましたが、分割したので無料でもお読みいただけるようになりました。 元

やまもと

もう少し高速になりました。｜行列積高速化＃２９

前回の記事で、OpenBLASよりも7~8%性能が劣っていました。その後、いろいろ試していたのですが、2~4%ほど高速になったので、性能が向上したポイントを記録しておこうと思います。 ピーク性能比率でみると95~97%、FLOPS値でみるとおよそ45GFLOPSくらいなりました。それでも、OpenBLASよりも劣っているので、まだ工夫の余地はあるのでしょう・・・。 プリフェッチの見直しカーネル関数のプリフェッチに関しては第18回で書いていますが、第25回でカーネル関数を書

やまもと

OpenBLAS, ATLAS, BLASとの性能比較｜行列積高速化#28

そこそこ高速な実装ができたので、他のBLASライブラリが持つDGEMMと性能比較を行ってみましょう。 比較を行うライブラリとしては、下記を使用しました。 １、BLAS（NetLibの参照実装） ２、ATLAS ３、OpenBLAS これらのライブラリについては、下記でも紹介しています。 GCCの準備評価環境として使用しているMacBookでは、OpenBLASはbrewでインストール可能でしたが、BLASとATLASは独自にコンパイルする必要がありました。 コンパイ

やまもと

転置行列コピー関数の改良｜行列積高速化#27

行列コピー関数は、行列積の計算量O(N^3)よりも計算コストが圧倒的に小さいことを利用して、以下の目的で導入しました。 （１）あらかじめ、行列データをキャッシュメモリに書き込んでおく （２）行列データを直列化し、行列積計算カーネルのキャッシュ利用効率を最大化 （３）DGEMMの転置オプションを行列コピー関数の差し替えで実現する これらに関しては、以下の記事をご参照ください。ただ、これらの記事は、実装や高速化にとって重要なポイントなので、有料記事にしています。 転置行列コ

やまもと

ブロッキングサイズの改良｜行列積高速化#26

当初の設計（下記の記事）では、I,J,Kループのキャッシュブロッキングサイズは、キャッシュメモリの容量に収まるように決めました。 しかし、L1キャッシュブロッキングの有無がカーネル関数の性能を左右していたため、性能実測しながらL1~L3のブロッキングサイズを変更することにしました。前回の記事のカーネル関数の性能は、ブロッキングサイズ改良後の測定値になります。 改良したブロッキングサイズ当初の設計では、キャッシュメモリのブロッキングサイズを下記のように設定していました。

やまもと

カーネル関数の性能推定と改良｜行列積高速化#25

ここまで、行列積の高速化チューニングの手順を書きましたが、サンプルが思ったよりも性能が出ませんでした。そこで、もう少し粘ってチューニングをしていましたが、なんとか理論ピーク性能比率で90%を超えたので、何をやったのか書き残しておこうと思います。 追記 （2020/11/14）下記記事の分割＆シリーズ化に伴い、タイトルを変更しました。 カーネル関数の作り直しサンプルを作成したのち、いろいろ計算速度を測定した結果、結局カーネル関数の実装が遅いのだろうという結論になりました。そ

やまもと

行列積の性能測定｜行列積高速化#24

この記事は、以下の記事を分割したものです。 ［元の記事］行列積計算を高速化してみる 一括で読みたい場合は、元の記事をご覧ください。 以上で、行列積DGEMMの最適化手続きは全て完了しました。思ったよりも性能は出ませんでしたが、いったんこの記事は終了にします。 それでは、最終的にどの程度高速化できたのかを確認します。 計算速度の行列サイズに対する依存性を見るために、NxNの正方行列を対象として基本周波数の理論ピーク性能比を、N=16,32,...,2048で測定しました。

やまもと

行列スケール関数の最適化｜行列積高速化#23

この記事は、以下の記事を分割したものです。 ［元の記事］行列積計算を高速化してみる 一括で読みたい場合は、元の記事をご覧ください。 スケール関数の最適化も、コピー関数の最適化と同じの手続きを進めます。ただ、スケール関数はまだアンローリングを行っていないため、アンローリングから始めます。また、計算時間は非常に短いため、今回はアライメントの場合分けを見送ります。 最適化の手続き （１）アンローリング （２）ベクトライズ、アセンブラ化 （３）プリフェッチの挿入 （４）ループシフ

¥100
やまもと

行列スケール関数のテストプログラム作成｜行列積高速化#22

この記事は、以下の記事を分割したものです。 ［元の記事］行列積計算を高速化してみる 一括で読みたい場合は、元の記事をご覧ください。 スケール関数は、下記の計算に使用します。 C = beta * C コピー関数と同様に、スケール関数も２つのテストプログラムを作成しておきます。 （１）処理結果確認プログラム・・・正解値と処理結果の比較 （２）処理速度測定プログラム・・・処理時間を測定 22-1. テスト用構造体行列積のテストプログラムと同様に、テストに必要な関数と引数

やまもと

行列コピー関数の最適化｜行列積高速化#21

この記事は、以下の記事を分割したものです。 ［元の記事］行列積計算を高速化してみる 一括で読みたい場合は、元の記事をご覧ください。 コピー関数の最適化の手続きは、行列積カーネルの手続きとほとんど同じです。唯一の違いは、コピー元である行列のアライメントが不明なため、アライメントが揃っている場合とそうでない場合で場合分けする点くらいです。 最適化の手続き （１）ベクトライズ、アセンブラ化 （２）プリフェッチの挿入 （３）ループシフト／命令順序の入れ換え （４）アライメントの場

¥100
やまもと

行列コピー関数のテストプログラム作成｜行列積高速化#20

この記事は、以下の記事を分割したものです。 ［元の記事］行列積計算を高速化してみる 一括で読みたい場合は、元の記事をご覧ください。 行列積のテストプログラムは現在のものを使えば良いですが、行列A,Bのコピー関数は、行列積計算に比べ処理時間が短すぎて、現在のテストプログラムだと性能が向上したかどうかがほとんど分かりません。 そこで、コピー関数は独自にテストプログラムを用意することにします。行列積計算の場合と同様に、それぞれ下記の2つのプログラムを作成します。 （１）処理結

やまもと

アセンブラ命令順序の最適化｜行列積高速化#19

この記事は、以下の記事を分割したものです。 ［元の記事］行列積計算を高速化してみる 一括で読みたい場合は、元の記事をご覧ください。 次に、各演算器の停止時間を最小化するために、５つの演算器を同時使用できる命令順序への変更を考えます。 今回のプログラムでは、FMA計算・ロード処理・詰め替え処理の３つを行っています。Skylake マイクロアーキテクチャでは、FMA計算は２つの演算器（port0, port1）、ロード処理も２つの演算器（port2, port3）、詰め替え処

¥100
やまもと

プリフェッチの挿入｜行列積高速化#18

この記事は、以下の記事を分割したものです。 ［元の記事］行列積計算を高速化してみる 一括で読みたい場合は、元の記事をご覧ください。 次に、メインメモリからキャッシュメモリにデータを運んでおくために、プリフェッチを挿入します。プリフェッチには、ハードウェア・プリフェッチとソフトウェア・プリフェッチがあります。 ハードウェア・プリフェッチ　＝　CPUが自動的に行うプリフェッチ ソフトウェア・プリフェッチ　＝　プリフェッチ命令で行うプリフェッチ プリフェッチ命令は自由に挿入で

やまもと

アセンブラによるベクトル化｜行列積高速化#17

この記事は、以下の記事を分割したものです。 ［元の記事］行列積計算を高速化してみる 一括で読みたい場合は、元の記事をご覧ください。 アセンブラ命令を選択したら、インラインアセンブラ機能を使ってプログラムを実装していきます。 前節では、MxNxKが4x4x8にアンロールされた場合だけを検討しましたが、実際には３×３×４＝３６通りの場合があります。 もっとも、K≧8, K&4, K&2, K&1のば場合の違いは、命令数が違うだけです。K≧8の場合さえ実装できてしまえば、K&

¥100
やまもと