
子ども集団の発達過程を数理的に分析するために(S字カーブのGompertz曲線への当てはめ)
子どもたちの中の達成度合を累積させたグラフからは、子どもの発達過程を数理的に分析する方法について考えてみました。
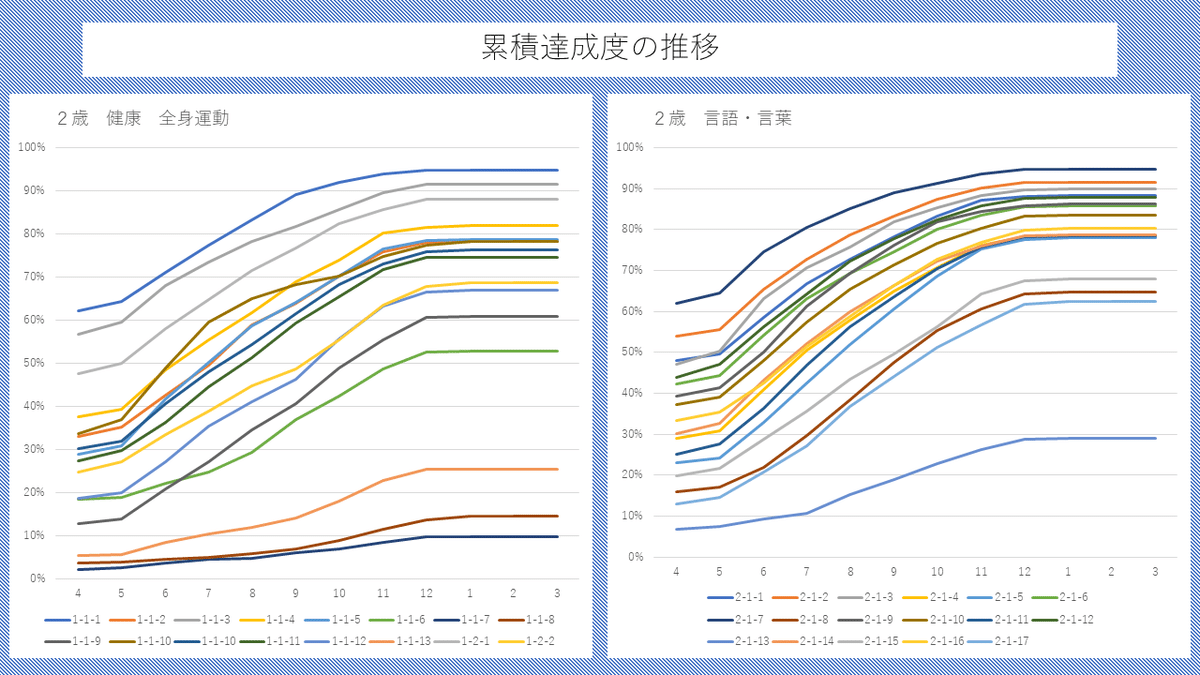
子どもの発達の累積変化の状況
これらのグラフは、子どもたちの発達経過記録から、毎月の発達の達成状況を記録対象の行動ごとにグラフにしたものだ。行動項目は、「健康:全身運動」「言語・言葉」領域の発達を示す行動から選んでいる。
それらの領域に属する行動項目ごとに、年度初めの4月(初期状態)の達成率(記録対象の子ども全体の人数に対する、「達成:○」が記録された子どもの比率)から始まって、年度末の3月までの各月において、累積達成度(その月の記録時点までに、「達成:○」が記録された子どもの比率)を折れ線グラフにしている。
これらのグラフを見ると、記録の対象となっている行動、例えば、「両足を揃えて階段を上る」「でんぐり返し(前転)ができる」「名前を呼ぶと返事ができる」「文字に興味を持つ」といった行動の累積達成率が、概ねS字カーブになっていることが見て取れる。つまり、最初の1、2ヶ月は、あまり大きな伸びは見られないが、年度の半ばの数ヶ月に急に「できる子」が増えていき、年度末の2、3ヶ月では、「できる子」の増加が見られなくなるという動きだ。
また、興味深いのは、初期状態で達成率が低い行動は、概ね低い累積達成度で推移しているということだ。つまり、折れ線グラフが途中でクロスすることは多少あるが、概ね平行的に動いているように見えることだ。累積達成率のスピードは、概ね先行する行動が、そのまま先行して、結局ゴールすることになるようである。
同時に、右の「言語・言葉」領域の折れ線グラフを見ると、初期状態で達成率が比較的高かった行動については、その累積達成率が、期末に向かって「収束」していく様子が見て取れる。
累積変化のパターン
さらに言えば、累積達成のS字カーブの動きに2つのタイプ、期首状態のバラツキが維持されるタイプ①と上限に「収束」していくタイプ②があるように見える。勿論、初期値が高く、年央の延びも大きいS字カーブは、結局「天井」にぶつかって、強制的に収束させられる一方、初期値が低いS字カーブは、強制収束の機序が作用しないので、バラツキが維持される又は時間とともに拡散していく機序がそのまま実現しているということなのだろう。
このようにグラフの形状の視覚的特徴を確認することだけでも、新しい発見がある。しかし、もっと定量的に、この折れ線グラフのパターンを分析してみたいところだ。そこで、折れ線グラフを表す数式、関数を考えてみたい。
この累積達成率のS字カーブの曲線は、一見すると、ロジスティック曲線のように見えるかもしれない。しかし、ロジスティック曲線のS字は点対称で逆さにしても同じ形になるはずだが、この累積達成率のS字カーブは対称的には見えない。とすれば、このような点対称でないS字カーブは、ゴンペルツ(Gompertz)曲線ではないかと思われる。
このゴンペルツ曲線とは、個体群の個体数の成長をシミュレートするものとして、良く分析に活用されるものであるが、個体の大きさの成長にも使われるほか、ソフトウェアのバグの発見数の確認にも使われている。具体的な式は、次のようになる。
![]()
この式において、Kは最終的にy(個体数 等)が近づいていく限界値であり、xが時間を表している。よって、x=0を代入した、yの初期値はK×bであり、0<b<1の元で、個体数の増加率は、時間とともに指数的に単調減少していくことになる。
一方、ロジスティック曲線を表す式は、次のようになる。

ロジスティック曲線は、個体数が大きくなるとと増加率が下がる作用があり、ゴンペルツ曲線では、時間とともに急速に増加率が小さくなるという、数式を構成する変数間の関係上の差がある。
ゴンペルツ曲線
さて、子ども集団における発達の達成率の動きが、ゴンベルツ曲線でシミュレートできるということは、どういうことなのだろうか。上のゴンペルツ曲線の式の形を決めているのは、K、b、cの3つの変数である。Kは上限値、bは初期値、そしてcは達成率の変化の傾きを決めている。先にグラフの視覚的読み取りで分類できたタイプ①(バラツキが維持される。平行的に推移する)は、bとKの関係が1体1対応になるが、タイプ②(上限値に収束)ではbとKの関係が1対多の対応関係になる。また、初期値が低いS字カーブは、期末の値も低い状態になっていることから、年央の達成状況の伸びが小さいということであり、これはcの値の大小に関連してくることになる。
これら3つのパラメータの値のちがいによって、記録する項目(記録対象行動)の発達、達成の特性を定量的に評価することができ、その特性に基づいて、行動をグルーピングすることで、時間の展開、言い換えれば、子ども集団自身の内的成熟のタイミングに配慮することができるようになるだろう。つまり、同じような達成スピードにある行動を、領域横断的に構成することができるだろう。また、Kやbとの関係を意識すれば、今は集団全員が達成しなくても、それ自体を問題視する必要がないということも分かってくるはずである。特に、累積達成率は必ず100%が上限だが、項目行動ごとのKは必ずしも100%ではないことが看取されるので、子ども集団の発達を見ていくときに「全員達成」を目指しては行けない行動があることが示唆されている。
さらに、今回は同年齢のクラスを一括して集計しているが、クラスや集団ごとのこれらのパラメータを計測することで、個々のクラス集団の達成パターンの特性を見いだすこともできるかも知れない。
子どもの発達の数理モデリングの可能性
ただ、この分析は、あくまで子ども集団を「集団」として把握している-生物学的に言えば個体群として把握しているものである。保育の専門性の根拠の一つに、子どもの集団としての変化への専門性があるべきであると筆者は考えており、このような子ども集団の変化を把握する技法の進化、浸透が、保育の質を上げていく上で必要な視点であると思っている。
他方で、このような分析は、個体群の分析であって、個々の子どもの変化のシミュレーションではないこと、そして、個々の子どもの達成や発達がこのように進むということを分析している訳ではないことは再確認したい。
生物現象に対する数理モデルの数学的解析を行う学問分野を『数理生物学』と言う。この数理生物学における数理モデルの位置づけとして、次の4つの範疇があり得るとされている(瀬野「数理生物学講義 基礎編」共立出版 2016年 p3)。
ア:具体的な生物現象の特定の側面を研究するための数理モデル
イ:生物現象の量的理解のための数理モデル
ウ:生物現象の質的理解のための数理モデル
エ:生物現象の知見の体系化のための数理モデル
(註:カタカナの割り振りは、引用者によるもの)
ア→エに向かうごとに、抽象度が高くなっていくと筆者は解釈している。
アの範疇のモデリングは、特定の行動の達成状況のシミュレーションで、与件の変化によって、特定の行動の達成率がどう変化するかということの研究となる。イのモデリングでは、子どもの行動達成に対し、あるパラメータの変化がどれ位の影響を及ぼすかという研究になろう。ウでは、パラメータの変化と達成率変化の方向性を研究し、エにおいては、そもそも発達達成に作用するパラメータが何なのかということを解明していくことになろう。
今回の作業は手元にあるデータに基づくものであり、過度の一般化は厳に慎む必要がある。とはいえ、子ども集団の変化、発達をこのように数理モデル化し、実際のデータの動きがどのようなモデルによって最も良く分析、解明、シミュレート(再現)できるのか、今後も引き続き研究を進め、想定もされていなかった特性や因果関係を見出せればと思っている。
