
授業協力への準備『平面図形の面積(四角形と三角形の面積)』:教材研究編
今年度も他校の研究授業の授業協力を引き受けることになりました。
毎年、どこかで授業協力をさせていただく機会をもらえることがとてもありがたいですし、授業協力する授業づくりに参加することによって自分自身も学びを深めていきたいと思っています。
授業協力する授業のうち、1つが5年生『四角形と三角形の面積』の単元だと聞きました。
『四角形と三角形の面積』の単元は、研究授業にも選びやすい場所だと思います。この単元の内容、ポイントを改めて整理して、授業公開する先生のやりたいことをサポートできるようにしていきます。
今回は『四角形と三角形の面積』の教材研究した内容を紹介します。
ざっくりとした全体像をまとめることで、授業検討会前後で深めていくところを見つけやすくすることが目的です。
1.本単元で学ぶこと
A:単元の概要と単元の流れ
「四角形と三角形の面積」の単元では、三角形、平行四辺形、ひし形、台形といった図形の面積の求め方について学習します。その際、4年生「面積」の単元で学習した長方形や正方形の面積の公式(「たて×よこ」「一辺×一辺」)と結びつけて考え、「底辺×高さ」などの公式としてまとめていきます。
つまり、全く新しい学習をするのではなく、以下のような順番の学習をそれぞれの図形で繰り返して進めることとなります。
未習の図形の求積の問題と出合う。
既習の図形の公式が使えないか考える。
面積を求める。
求めるときに使った数値から、未習の図形のどの箇所の数値を使えば良いか振り返る。
公式化する。
特に、5の「公式化」にあたっては、1問だけ解いてそれが本当に公式と呼べるのかという点は気をつけたいものです。学習指導要領でも以下のように触れられています。
さらに、いつでも同じ要素などに着目することで、面積を求めることができるかどうかを確かめることによって、公式として導いていけるようにする。
先行知識がある子も多いはずなので、すんなり「底辺×高さ」などとまとめてしまいたくなる気持ちも分かりますが、「同じ形で長さが違う問題でも同じ方法が使えるのかな?」などと、適宜問い返していくことで「これは公式と言えるだろう」という納得感を多くの子に生みながら進めていく必要があります。
また、単元の流れは以下の順番がオーソドックスです。
平行四辺形
三角形
台形
ひし形
およその面積
これは、平行四辺形を2等分すると三角形になる点を活かした構成となっています。そのため、平行四辺形で「底辺×高さ」を公式化すれば、三角形は「平行四辺形の半分なので÷2すればよい」と簡単にまとめることができるのです。
一方、平行四辺形と三角形を逆の順番で扱う構成の場合もあります。この構成について大野は以下のように指摘しています。
直角三角形の求積は、「長方形の半分」と容易に気づけるということである。そして、直角三角形の求積方法を見出せれば、二等辺三角形や鋭角三角形も分割することで直角三角形に帰着できるので、求積方法を見出すことができる。
この指摘からは、既習である長方形に帰着する考え方に違いがあることが分かります。平行四辺形から扱う場合は「等積変形」で、三角形から扱う場合は「倍積変形」が結び付くことになります。
どちらから進める方が子どもたちにとって良いといえるか。公式化していくための子どもの思考の流れを具体的にイメージをして単元を展開していく必要がありそうです。
※「等積変形」「倍積変形」については、後ほど説明します。
B:単元内の子どものつまずきについて
それでは、単元の中で子どもはどこにつまずくのでしょうか。盛山は「経験的にもつイメージや思い込みのこと」を「誤概念(ミスコンセプション)」とし、2つの場面を指摘しています。
1つ目は、長方形を傾けて平行四辺形にしたとき、面積が変わらないというミスコンセプションです。以下の図のような場合です。
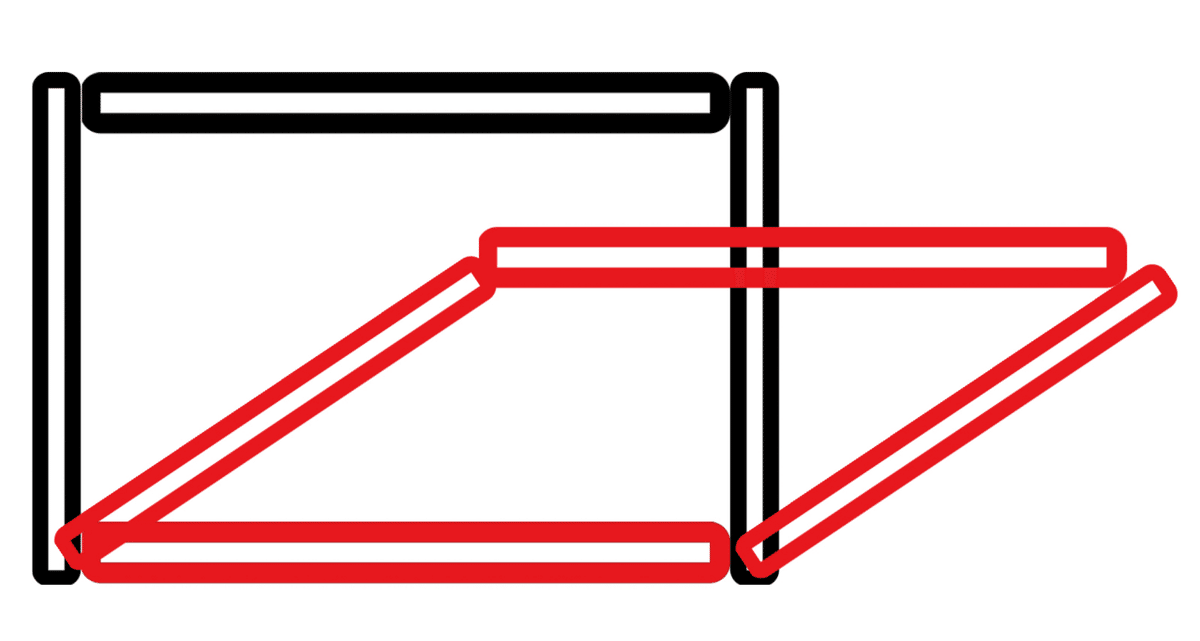
2つを見比べるだけでは、同じ面積だと感じてしまう子がいます。盛山は赤の図をさらに倒していくことで面積が減ることを理解できるとしています。
2点目は「高さ」に関するミスコンセプションです。平行四辺形や三角形の公式に使う「高さ」は「底辺から垂直に伸ばした直線の長さ」のことです。そこを「斜めの辺の長さ」として計算してしまうのです。

これらのことからも、単に「底辺×高さ÷2」などの公式を扱うのではなく、高さを含めた必要な数値を見いだす場面を扱い、「どこを高さと見れば良いのか?」「そもそも「高さ」とはどういうものだったか?」を考えていく場面を意図的に設定していく必要があります。
2.本単元で引き出したい考え方
それでは、「四角形と三角形の面積」の学習を進める上で引き出したい子どもの考えについて触れていきます。それは、「等積変形」「倍積変形」「分割」の考えです。この考えは、学習指導要領解説にも明記されています。
数学的な見方・考え方を働かせることで、例えば次のような考えが導かれる。
①図形の一部を移動して、計算による求積が可能な図形に等積変形する考え
②既習の計算による宮跡が可能な図形の半分の面積であるとみる考え
③既習の計算による求積が可能な図形に分割する考え
簡単にまとめると、①が「等積変形」②が「倍積変形」③が「分割」の考えです。

これらを踏まえて、この単元で働かせる「数学的な見方・考え方」を言語化していくと、この単元での「図形の見方(を働かせる)」とは「求積する図形を既習の図形に変形・分割可能であるという視点でみること」で、「考え方」は「図形に変形・分割することで既習の求積公式を適用できないかと考えること」というように表現できそうです。さらに、「辺の長さ等が変わった図形でも、同様に求める方法がないか考えること(公式化の考え)」も含まれるはずです。
3.「公式として導くこと」について
「四角形と三角形の面積」の単元は学習指導要領上では、「平面図形の面積」とされています。その中の思考力・判断力・表現力等の目標を参照すると、「図形を構成する要素などに着目して、基本図形の面積の求め方を見いだすとともに、その表現を振り返り、簡潔かつ的確な表現に高め、公式として導くこと」となっています。
つまり、すぐに公式化するのではなく、どの考え方が面積を求めやすいのかを検討したり振り返ったりする場が必要となります。
加えて、「平行四辺形→三角形→台形→ひし形」と公式化のサイクルと繰り返すわけですから、どの考えが公式化に導きやすいのかまで検討できると良いのではないかと思います。
ちなみに、公式を整理すると以下のようになります。
平行四辺形の面積=底辺×高さ
三角形の面積=底辺×高さ÷2
台形の面積=(上底+下底)×高さ÷2
ひし形の面積=対角線×対角線÷2
これらの公式の基となる考え方は、平行四辺形以外「倍積変形」となります。その点を意識すると、子どもたちも「公式化は倍積変形」と考え、単元が進むにつれて公式化前提として倍積変形に取り組むようになっていきます。
※その実践は別の機会に紹介します。
そして、もう一つ。
この面積の公式、他の公式との関係性を考えると面白いのです。
例えば、底辺が3cm、高さが4cmの平行四辺形だとします。
平行四辺形の公式:3×4=12
台形の公式:(3+3)×4÷2=12
もう一つ、底辺が3cm、高さが4cmの三角形だとします。
三角形の公式:3×4÷2=6
台形の公式:(3+0)×4÷2=6
三角形は上底を0cmとして考えていますが、2つの例からも平行四辺形と三角形は台形の公式でも求めることができます。
ただ、公式を考えるだけではなく、その公式同士の関係性まで捉えられるようにすると、公式化することの楽しさ、面積を求めることの楽しさにもつながってくると思えるはずです。
余談ですが、私が授業していたクラスでは「台形の公式で全部まとめられる」と考えていた矢先に、「ひし形の公式で台形が求められる!」という発見をする子がいました。最終的に「ある条件」が満たされないと適用できないことを見付け、私自身も新しい発見でした。
以上が「四角形と三角形の面積」の単元の教材研究のまとめとなります。
大まかで良いのでまずは全体像をつかみ、ここから先行実践等を調べてさらに深めていこうと思います。
どこかのタイミングで、自分の授業も板書での振り返りも投稿します。
ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
