
5年『四角形と三角形の面積』のデザイン④:ひし形、四角形、およその面積まで学習を進め、子どもたちが見いだしたこと
5年生「四角形と三角形の面積」の単元の紹介も4回目となりました。
ひし形、一般四角形、およその面積と進める単元終盤の内容です。
これまでの学習で、子どもたちは「公式化をしたい!」という思いをもって面積の求め方を考えることを通して公式化への道筋を学び、そこから「台形の面積の公式が最強だ!三角形にも四角形にも使える!」と公式に対する見方を変化させてきています。
学習の終盤では、以下のような子どもの姿が引き出されました。
ひし形の求積公式と台形の求積公式の関係を考える子
多角形の面積を考える子
およその面積の考え方を用いて円の面積の公式化を導こうとする子
もちろん学級の子ども全員がこのような姿になっているのではありませんが、上のような子どもたちは、学び取ったことを武器に、探究したいことを自分の手で考え始めるようになりました。
そこに、集団で学び、集団で知識を構成していくことの価値と可能性があります。
教科書にある内容を「ただ理解する」体験ではありません。
教科書にある内容を「創り出す」体験です。
特殊な授業のように見えますが、実際は教科書の問題を活用した日常の授業です。
もしよければ過去の記事も御覧ください。
①9時間目:ひし形になり、改めて「平行の組の数」に着目する子ども

授業の導入ではすぐにひし形を提示します。
板書左側のふきだしにもある通り、「台形の公式で分かりそう!」「等積変形でできるんじゃない?」と既にその解決方法を考え始めています。
自力解決に入り、子どもの考えがはっきりしたところで交流に入ります。
板書には以下のような考えが出されます。
長方形にする(等積変形):中央左上
分割して三角形2つにする(分割):中央上 ※台形の公式を利用している
ひし形を内接する長方形にする(倍積変形):右側上
長方形にする(等積変形):右端上
分割して三角形4つにする(分割):中央下
長方形にする(等積変形):右下
この6種類が出された考えです。
単元終盤ということもあり、どの考え方も出されています。
一つひとつの考えを子どもたちと読み取っていきます。
ここで面白いのは、台形の公式を適用して説明する考えがいくつか出されていることです。前回の「台形の公式最強!」の意識が残っていることが分かります。
全ての考えの読み取りが終わると、「公式はどう考えられるかな?」と問います。
子どもたちは既に「公式化するなら倍積変形」と考えているので、「ひし形を内接する長方形」の考えから公式を導き出そうとします。
長方形の「たて」と「よこ」はひし形のどこの長さと同じなのか?
そう考えることで、「たて」×「よこ」は「対角線の長さ」×「対角線の長さ」だと見えてきます。あとは「倍積変形なので「÷2」だね」ということで公式化は終了です。
すんなり終わる内容です。
子どもたちは振り返りを書きながら「先生だったら、どうやってこの問題解く?」と質問してきました。そこで出したのが板書の左端の等積変形の考えです。平行線を引き向かい合う頂点を並行移動させることで三角形に等積変形できます。そうすると、「対角線の長さ×対角線の長さ÷2」は「底辺×高さ÷2」だということも見えてきます。
振り返りのノートを見ていると、同様の方法で三角形ではなく平行四辺形に等積変形している子がいたことに後で気がつきました。平行四辺形に変形すると「対角線の長さ×対角線の長さ÷2」は「(底辺÷2)×高さ」となります。(高さ÷2にすることも可能)その子のことを取り上げれば、更にクラスの仲間への意識が高まりそうだったので反省です。
今回はひし形の公式が分かりました。台形の公式って1つの組が平行ならいいんだから、円じゃなければ全ての図形に(で)1組の平行がある(なら)台形の公式=図形の公式だと思いました。
台形の公式はどんな図形でもできるから、図形の公式としてまとめたいと思った。対角線×対角線÷2を公式化どうか確かめるために違う角度のひし形や横が長いひし形でもやってみたい。
この授業の後、「ひし形の求積公式が台形にも適用できるのか?」という疑問をもった子がいました。その子と一緒に台形を描きながら考えていると、対角線が直交する台形はひし形の求積公式が適用できることが分かってきました。
四角形の面積は以下の様に求められます。(noteでは分数の表記が難しいのでこの様な表記にしています。)
S=対角線×対角線×sinθ÷2
詳しい証明はいろいろな所で紹介されているのでそちらを参考にしてください。(例として挙げておきます。)
対角線が直交している場合は、sin90°となりますのでsin90°=1と考え、S=対角線×対角線÷2で計算できるということです。
②10時間目:「対角線(じゃないけど)×対角線(じゃないけど)÷2」

さて、次の授業は四角形(「一般四角形」とも呼ぶ場合がありそうですが)です。
子どもたちの振り返りを見ると、今までの四角形は平行な辺の組があることへの着目がありました。今回はその平行な辺の組がありません。それでも「できそう!」と子どもたちは考え始めます。
自力解決後の交流で出された考えは6種類です。左から順番に紹介すると
分割して三角形2つにする(分割)
四角形を内接する長方形と考える(倍積変形)
分割した片方の三角形を等積変形し、三角形にする(等積変形) ※不正確
分割して長方形にし、残りを倍積変形する(分割)
細々と等積変形して面積を数える(等積変形)
四角形を内接する長方形と考える(倍積変形)
子どもたちは答えまで辿り着けましたが、その解決方法を見ると少し苦労している様子です。しかし、解決方法が出されるとその考え方はこれまでの既習の活用なので難しくはありません。それぞれの考えの説明を聞いて「そう考えればいいね!」と子どもたちと確認していきます。
面白かったのは、2と6の考えの時です。
2の考えを発表してくれた子は、「対角線じゃないけど対角線が見える」と言いながら図形の中央部分に線を引きました。子どもたちは「???」という感じでしたが、その子(4+4)が四角形を内接する長方形の横の長さであり、もう一方の対角線が縦の長さだと言いたかったようです。
子どもたちは「倍積変形だ!」とまとめていきましたが、先ほど紹介した「対角線×対角線(×sinθ)÷2」の公式の適用と考えることができます。
四角形を内接する長方形の辺に沿って頂点を移動すれば対角線を直交させることができるからです。
ここまでは流石に触れきれず、「対角線(じゃないけど)×対角線(じゃないけど)÷2のような計算でできるね!」という様にまとめていきました。
③11時間目:「この方法を使えば円の面積も求め方の規則性が見えるんじゃない!?」
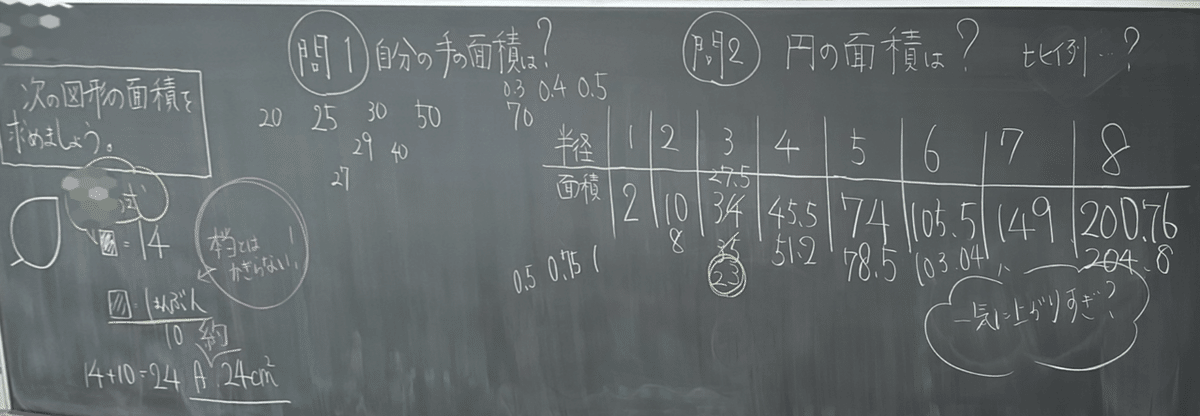
さて、単元最後の時間です。(板書が相当やる気がなさそうに見える板書で載せるのを躊躇いました。)
教科書の内容では「およその面積」です。葉っぱの形をマス目を用いて1個分と0.5個分と分けて数えるという問題を解きます。簡単すぎると思っていたのですが、これまで10時間を一緒に学習していた子どもたちが見せる姿は一味違いました。
始めの15分はこの問題を一緒に解いていました。
正確ではないという部分どう考えるかを話し合っていたときに、「本当とは限らないけど、半分(0.5)として数えればよい」と発言した子のアイデアから、ある子が「その考えを使えば円の面積が求められる!」と急に言い始めました。その発言に複数の児童が刺激を受けた反応を見せます。
答えを確認した後、子どもたちに「もう一問問題を用意しておいたけど、どうしたい?」と問いかけてみました。
その問題を解きたい子と円の面積について考えたい子が半分ぐらいの割合でした。
私が用意した問題は、方眼紙に手を形取り自分の手の面積を求めるものです。この問題は予め予想しておくと、自分の量感が揺さぶられるところが面白いです。
円の面積を考えたい子どもたちは、その方眼紙に円をかいて面積を考え始めました。先ほど「円の面積が求められる!」といった子に、どのように考えるかの話を聞いていると、「僕は、半径か直径が関係していると思うから、長さを変えて表に整理すると比例のような関係性が見えて公式にできるのではないか。」と教えてくれました。
ともすると「円の面積の公式知らないの?」と思われるかもしれません。しかし、この子は知っていることよりも大切な「考えるためのプロセス」を身に付けています。
円の面積を考える子でそれぞれの半径で分担して求めること提案すると、子どもたちにも熱が入ります。果たして規則性が見えるのか。その結果が右側の表でした。さすがに規則性がなかなか見えなかったようです。
S1=r×r×π
S2=(r+1)×(r+1)×π
=(r×r+2r+1)×π
=r×r×π+(2r+1)×π
少し考えてみますと、半径rの円(S1)と半径を1cm増やした円(S2)の面積は(2r+1)×π分大きくなります。この差に着目するのは流石に難しいです。
「どんな方法を使えば簡単に円の面積を求めることができるのだろう?」と子どもたちは考えながら授業が終わりました。
授業後の休み時間、先ほどの子が私のところまでやってきて試行錯誤の成果を教えてくれました。

なにか見えそうだけど、見えない。だけど、何かが見えそう。
彼が話している様子からもどかしさが伝わってきます。その子は助け舟をあまり必要としない子なので「うんうん」と聞くだけです。きっと次の学年で円の面積を扱ったときにすっきりしてくれることを願っています。
長くなりましたが、以上が「四角形と三角形の面積」の授業でした。
始めは問題に関連する範囲で行われていた思考が、単元が進むにつれてどんどん広がっていった様子が伝わったでしょうか。
「個別最適化」「自由進度学習」「学び方を学ぶ」など、様々な言葉が出てきていますが、私は「集団での学び」こそ大切にされる必要があると考えています。
それは、「考えることで世界を自分の手で広げられること」「他者の考えに触れることで自分の世界が広がること」を感覚的に掴むことが大切だと思うからです。
ある子の問いを自分の問いにすることで「問い方」を学びます。
ある子の考え方を自分で使ってみることで「考え方」を学びます。
ある子の困り方を理解することで「人と人の違い」を学びます。
多様な子どもたちが混ざり合う中で、学びは生まれていくものです。
もちろん、学びの先に自分の追究したいことが生まれ、自分の手で考えていくことも同時に尊重される必要があります。
個別の学びは「集団の中で、その子を思いを尊重する学び」なはずですから。
最後まで読んでいただき、ありがとうございました。
この記事が気に入ったらサポートをしてみませんか?
