
ペントミノパズルって、面白い!
みなさんどうも、うつろです。
なるべく毎日2本投稿を続けているふつうの人です。ちなみに一応、本名・性別不詳でやらせてもらっています。
創作大賞2023ということで、これまで出してきた記事の総集編をご紹介。せっかくいただいたチャンスですからモノにしたいということで、ペントミノパズルという非常に興味深いエンターテインメントについて、これまでの投稿全11回の集大成をこの記事に全て注ぎ込みます。
ちょっと長いですがぜひ読んでみてください。
それでは本編。
ペントミノパズルとは
ペントミノパズルとは、5個の正方形が繋がった12個の異なる図形を6×10マスのプレートに隙間なく敷き詰めるパズルです。五角形のことをペンタゴンって言いますよね、その接頭辞です。
これ、実は答えが複数あるタイプのパズルです。具体的な数を出しますと、2,339通りであることが知られています。偶数ではないことを考えると、裏返したものを別の解と言ってはいけません。
それから余談ですがこの数、実は素数。この数字にどんな意味があるのかはいまだにわかっていないようです。
12個の図形はそれぞれ下の通り。形状からイメージされるアルファベットの名前で呼ばれています。真っ白だと味気ないのでピース専用の色も完全なる主観で決めました。以降は各ミノの名称を積極的に使っていきますので今のうちに覚えておくと楽です。個人的にはZミノとNミノ以外は割と分かりやすいんじゃないかと思います。

茶:Wミノ 赤:Pミノ ピンク:Nミノ 肌色:Fミノ オレンジ:Lミノ 黄:Xミノ
黄緑:Vミノ 緑:Yミノ 水色:Zミノ 青:Uミノ 紫:Tミノ 黒:Iミノ
偶然の出会い
私とペントミノパズルとの出会いは小学生の頃に遡ります。
ハナヤマさんの出しているペントミノパズルである「明治ミルクチョコレートパズル」をたまたま見つけた私。気になって遊び始めたところまでは良かったのですが、元の敷き詰め方を確認しないまま後先考えず始めてしまったため、見つけたその日にはピッタリ埋めることができませんでした。
その悔しさから「絶対にピッタリ埋めてやる!」と強い覚悟を決めてパズルに取り組むと、だんだんと解が見つかるようになってきました。そこで今度は、解を全て見つけてやろうと意気込み始めた私。ノートに見つけた解とその番号を書き記し、恐ろしく過酷な「2,339個書くまで終われません」がスタートしました。
これもひとつのアプローチ
ちなみに答え合わせをしておくと、とっくの昔にこのチャレンジは諦めています。もう解は全部見つかっていたからです。優秀なプログラマーさんが全ての解を算出するプログラムを一般公開していました。下のサイトから飛べます。
https://hamadajuku.com/column/math/archive/pentomino.html
このサイトを見つけるまで、私は独自の手法でペントミノパズルの解の発見を効率化してきました。今回お話ししたいのはこの効率化の手法についてです。
「え、全部見つかってるんだからそんなの意味ないんじゃないの?」と言いたくなってしまった、そこのあなた。まあ実際その通りです。
でもかの有名なナンプレ (数独) だって、プログラミングを使えばすぐ答えなんて出てしまいますよね?世の中答えがわかればいいってものばかりじゃないと思うんです。地道に解を探していくアプローチも、このパズルのプレイ方法としては至って真面目で、正攻法だと思うわけです。
私とペントミノパズルの出会いについて、詳しくは下の記事に書いています。よければ読んでみてください。
解の発見の効率化の手法について
ここからは本題に移っていきます。効率化と一括りに言ってもどういうことなのかわからないと思いますので、ひとつひとつ順を追ってやっていきましょう。
今回用いるのはこんな解。ここからずっと使うので解Xという名前でもつけておきましょうか。

これからこの解に含まれている特徴的な図形をピックアップし、それによって解の発見を効率化する手法をご説明していきます。私の造語なのですが、このような特徴的な図形をまとめて特殊組と呼んでいます。
効率化① 線対称な図形を探す
解の発見の効率化の第一歩は、解の中に線対称な図形がないか確認すること。もし線対称な図形が含まれていたら、その図形のみをひっくり返したものも別の解と言えることになります。解Xで探してみると、左上のLミノ、Uミノ、Xミノでできた4×4の正方形の1つの角を取ったような形が線対称になっているのがわかります。
しかしさらによく見てみると、Xミノがなくても線対称な図形になることがわかりますね。LミノとUミノでできた2ピース構成の線対称な図形ということになります。したがってこれを裏返した形はもちろん、別の解です。解を1つ見つけただけだと思ったら、2つ目が早くも見つかってしまいました。


詳しくは下の記事をご覧ください。2ピース構成の線対称な図形一覧のほか、線対称な図形が複数含まれる場合や、3ピース構成の線対称な図形についても紹介しています。
効率化② 線対称な図形 (大) を探す
①と似たアプローチです。先ほどは2ピースのミノで構成された比較的小さな図形をひっくり返しましたが、探してみると案外大きいものもあるようです。これは私の作った造語なのですが、4ピース以上で構成された線対称な図形を特別に巨大線対称と呼んでいます。

解Xで探してみると、今度は右の方にありました。Tミノ、Iミノ、Wミノ、Zミノ、Nミノ、Vミノ、Yミノでできた合計7ピースの非常に巨大な形です。これを対称軸で裏返したものも、もちろん解Xとは異なる解になりますね。
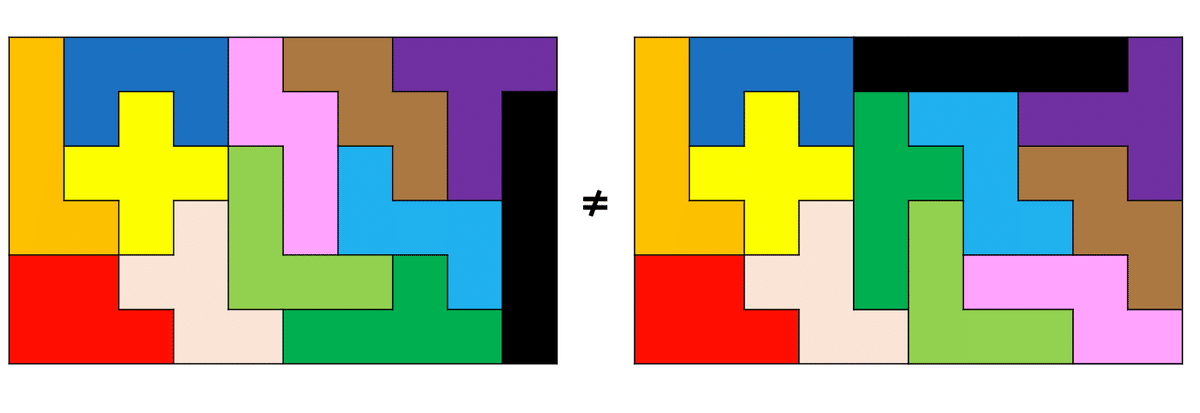
さらに詳しい説明は下の記事に書いています。興味があれば読んでみてください。
効率化③ 入れ換え可能な図形を探す
次は入れ換え可能な図形がないか探してみましょう。これも私が作った言葉です。
ひとつの解の中に同じ形が複数含まれているとき、この2つの図形を入れ換えたものは別の解になります。ちょっとわかりにくいかと思いますので解Xで探してみましょう。
下のイラストを見るとわかるように、Pミノ・Lミノでできた図形とTミノ・Iミノでできた図形は同じ形ですね。したがってこれを入れ換えたものは解Xとは異なる解とみなすことができます。

詳しくはこちらでも紹介してます。割と記事の評判が良かった印象です。
効率化④ 組み換え可能な図形を探す
最後の効率化は少々難しめです。組み換え可能な図形というのはこちらも私の造語で、線対称でないにもかかわらず2通りの方法で配置できる図形のことを指します。下の形を見るとわかりやすいかと思います。

さあ、解Xでも探してみましょう。見つかりますか?
ヒント: 3ピース構成です

答え合わせです。
Wミノ、Nミノ、Zミノでできた形が組み換え可能な図形となっています。ちょっとわかりにくかったかな。

したがって毎度のことになりますが、これを組み換えたものも別の解ということになるわけですね。
詳しくはこちらも参考になさってください。
ちなみにここまで点対称な図形についての記述はありませんでしたね。点対称な図形はさまざまな事情からペントミノパズルにおいては現れにくいんです。4ピース構成の大きなものについてはいくつか発見例がありますが、その使用例もかなり限られています。
こちらに関しても以下の記事でまとめておりますのでご覧ください。
結局解はいくつ見つかったのか?
ここまで解の発見の効率化についてご紹介してきました。それでは結局解Xから合計どれくらいの数の解が見つかったのか、見ていきましょう。
特殊組を組み換えることで新たな特殊組が生まれることも
下のイラストは上述の入れ換え可能な図形を入れ換えた時の解になります。ご覧のように入れ換えることで新たな線対称な図形と組み換え可能な図形が現れ、さらに見つかる解が増えることになりました。

このように要素が増えすぎると処理もしにくくなりますから、どうにかして全部の解を1つの表みたいなものでまとめる必要が出てきます。
全ての解をまとめる方法
全ての解をまとめる方法としてそれぞれの解を実際に書いて関係性を線で結ぶことができるとベストなのですが、いかんせんスペースもとりますし何より解を書くのにはかなりの時間がかかる。
このような理由から、解Xから派生した解のいずれかに含まれる特殊組を番号づけし、番号を記したセル同士の関連性を線で結ぶという方策を取ることにしました。

今回紹介する解では全部で14個の特殊組が関わっています。それぞれ上のイラストで示した状態を基本形とし、当該の特殊組に対してピースの移動が起こっている場合にはその番号に下線を引くことにしました。
3は巨大線対称を示しています。内部の構造が複雑に変化することから、今回はYミノの存在場所によって場合わけを行うことにしました。また10の線対称な図形についてはピースの配置の仕方が2つではないため、10-1から10-4までそれぞれ番号を決めることにしました。
実際にできた表はこちら
上記のルールをもとに作ってみた表がこちらになります。それぞれの線は解に含まれるいずれかの特殊組を入れ換えることによる変化を表しています。

一番左にある「1,2,3,4」と書いてあるセルが解Xを表しているものになります。したがってこの表から、解Xから派生する解の総数は全部で45個にのぼることが明らかになりました!
と言っても数字の羅列でしかありませんからイメージはしにくいかもしれません。ペントミノパズルを持っている方は実際に特殊組を動かして遊んでみてください。
特殊組を活用することで大量の解が見つかった例をもうひとつ別の記事で紹介しています。こちらも併せてご理解の手助けになればと思います。
おわりに
ここまでペントミノパズルの解について、1つの解をピックアップしてお話ししてきました。途中わかりにくいところやイメージしにくい部分があったかもしれません。もしそうだとしたら、それはこの記事を書いている私の責任ですのでお気になさらないでください。ご質問のコメントもお待ちしております。
ということで最後はペントミノパズル全体に立ち返ってもう少しお話をさせていただきます。
現在の目標と今になって思うこと
お話ししたとおりペントミノパズルの解はプログラミングによって全て判明しています。その上で私が特殊組を用いた解の効率化の手法を模索するのは、上に書いたような表をもとにしてそれぞれの解の関連性を明らかにしたいと思ったからです。
プログラミングで解を2,339通り見つけることが2,339人の顔と名前を覚えることであるとするなら、私がしたいのはその2,339人の相関図を書くことなんです。これは非常に時間と労力を要することだと思いますが、死ぬまでに成し遂げたいと思っています。
それから今になって思うのが、「組み換え可能な図形は恐ろしい」ということ。2ピース構成だと少ないのですが、3ピース構成、また4ピース構成ともなると大量の組み換え可能な図形が見つかります。そしてこれらには形やピースの種類に一切制限がありません。延々と見つかり続ける組み換え可能な図形はもはや狂気です。せめて "組み換え可能な図形は3ピース構成まで" と定めるべきだったかもしれないと今になって後悔しています。
現在の目標について詳しくお話ししているのが以下の記事になります。こちらも併せてどうぞ。
なぜこんなことをやっているのか?
最後になぜこんなことをやっているのか、その根本についてお話ししましょう。
今まで書いてきたことは教科書にも本にも、まして私のnote以外のネット記事にも一切載っていないことだと思います。そんな未知のことであっても、その気になればひとつくらいは研究することができるんです。
大学の研究室に行かなくたって、企業の研究職に就かなくたって、自分だけが知っている何かを作り出すことができます。そしてそれがいつか自分の人生の役に立つかもしれない。実際私はnoteを始めて、自分のやってきた成果を書くことができています。気になったらとことん調べて、理解を深めてみてください。私から皆さんに送りたいエールです。
補足資料
今回の記事ではご紹介できなかった内容を下にまとめています。興味を持たれた方はリンクから飛んでみてください。
謝辞
この記事を書くにあたり、最初期にさまざまな意見とモチベーションをくれた私の姉に多大なる感謝を述べさせていただきます。姉がいなければこのような記事を書くまでの知識には至らなかったと言って間違いないでしょう。
いや〜、長かったですね。私も5,000字を超える記事を書いたのは初めてでしたのでかなり疲れました。
スキ、コメントを心よりお待ちしています。内容についてご質問いただいた場合はこの記事に返信いたしますのでお待ちいただけると幸いです。
それではこのへんで。
いいなと思ったら応援しよう!

