
【革命】ベルトランのパラドックスについて
こんにちは。
皆さんはパラドックスをご存知でしょうか。
詳しい説明はWikipediaをご参照していただきたいのですが、要するに、
変なやつ
です。
一番有名なのは自己言及のパラドックスでしょうか。
「私は嘘つきである」
ですね。
仮に本当だとすると、自分が嘘つきとなり、本当ではなくなってしまう。
逆に嘘だとすると、自分は正直者になり、嘘でなくなってしまう。
そんな感じです。

さて、軽くパラドックスのおさらいをしたところで本題。
ベルトランのパラドックス
についてお話します。
ベルトランのパラドックスとは図形と確率のパラドックスです。
ざっくりいうと、円があって

円にすべての頂点が内接する正三角形を描き、
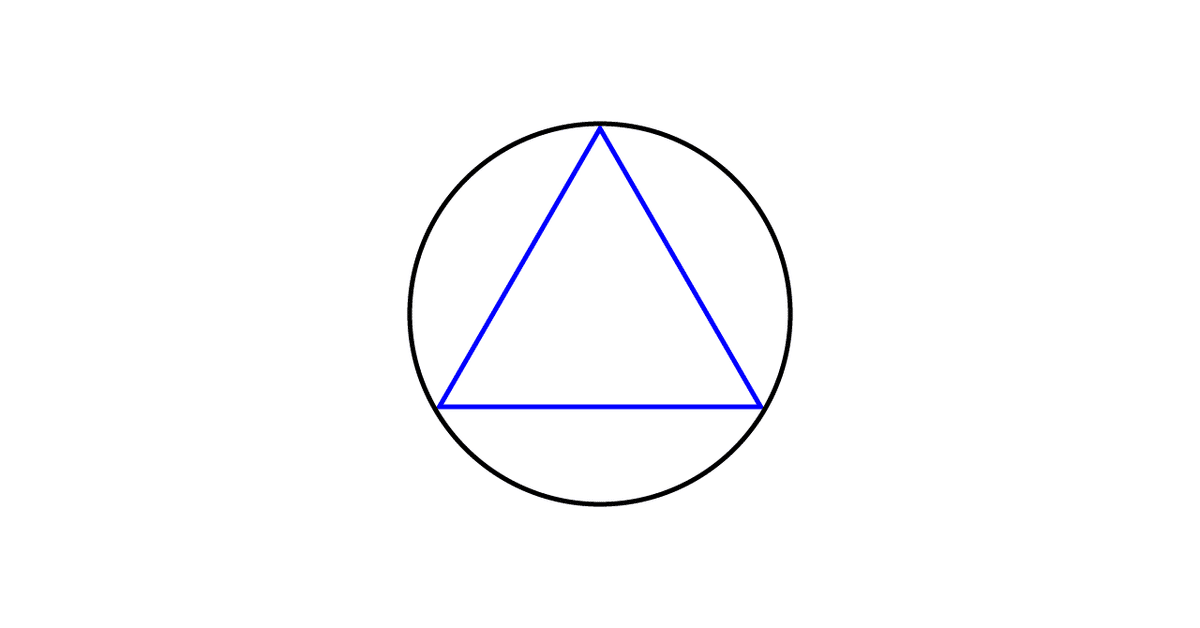
円周上に無作為な二点を選び、線を描きます。
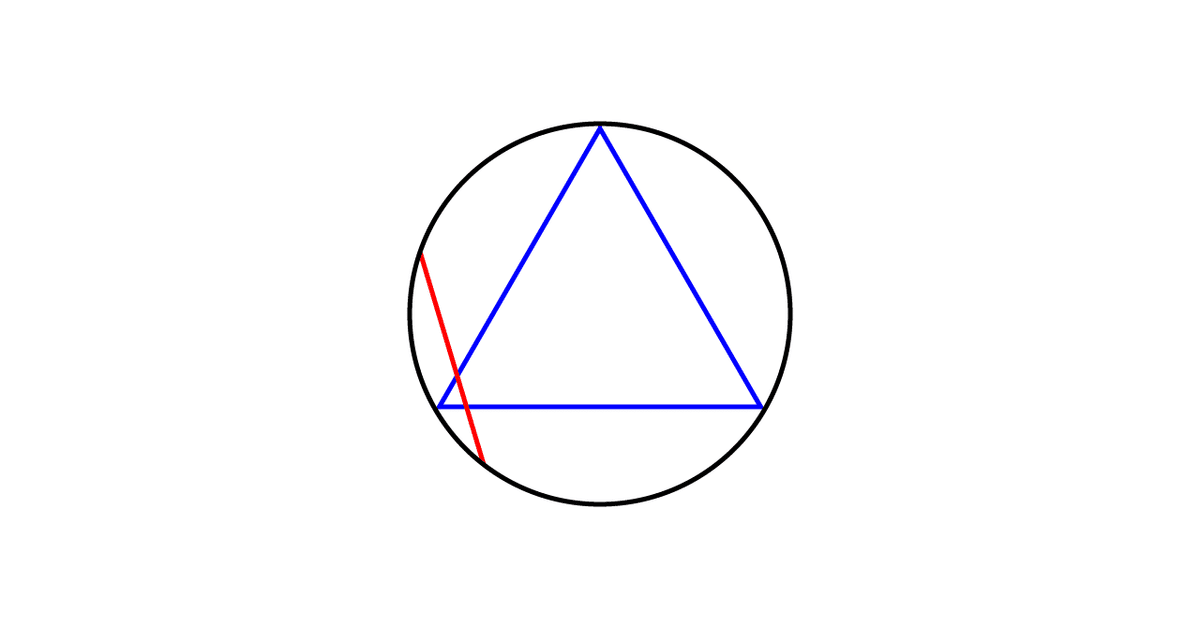
このような状態の時、赤い線の長さが青い正三角形の一辺の長さより多い確率を求める、という問題です。
一見簡単そうなのですが、数学者たちを悩ませたようです。
なぜでしょう。
結論から言うと、
選び方1だと、$${\frac{1}{2}}$$
選び方2だと、$${\frac{1}{3}}$$
選び方3だと、$${\frac{1}{4}}$$
が答えがなります。
詳しくはWikipediaをご参照。
しかし、どれかの方法が正解、なんてことはありません。
ではなぜこの違いが生まれてしまうのでしょうか。
それは、無作為に選ぶの定義が曖昧だからです。
は?
そう思いますよね。
よーくわかります。
でもね、
わかんなくてもいいのさ。
ともかく、変なことが起きているのです。
そこでコンピュータのちからを使ってどれが正しい答えなのかをしらべてみましょう。
詳しい説明は省きますが、sin cosや三平方の定理を使って計算させました。
$${\frac{1}{3}}$$に落ち着きましたね。
ということは選び方2が正しかった…
とも言えないんですね。
なぜならプログラミング上でも「乱数」を使っているからです。
どういうことかと言うと、「乱数」の出し方を明確に示していないのです。
つまり、あくまで「確率」であり、「偶然」でもあるのです。
選び方2は長さを使っているのですが、このプログラムはランダムを使っています。
つまり、たまたま答えが一緒であり、選び方2が正しかったとは言えません。
また、僕は数学者でもなんでもないヒトなので、正しいかもわかりません。
でも、自分の中では満足しています。
なんかまとまりのない文章になっちゃいました。
でも言いたいのは、
考えることが大事。
いいなと思ったら応援しよう!

