
#2 この1問!三角形の内角~三角関数の和積変換~
問題
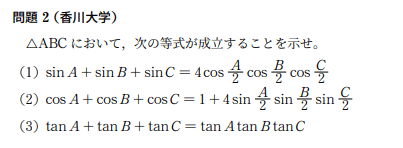
とりあえず,問題を解いてみてくださいね!
テーマ
三角形の内角の和に関する,等式の証明問題ですね。(1)(2)はともに同様のアプローチです。解ける気がしないようであれば,とりあえず(1)の解説を読んでみて(2)は自力で再チャレンジしてみるのが効率的かもしれません。三角関数の計算が丁寧にできる必要があります。
解答

1つずつの式変形の根拠や考え方を整理しておきましょう。三角形の内角の和に関する問題では,次のアプローチが基本になります。
$${A+B+C=\pi}$$より
1文字消去$${C=\pi-(A+B)}$$
1文字減少$${A+B=\pi-C}$$
積和・和積変換
そうはいっても1つずつの式変形が難しいですよね。まず式(1)については次のように考えて,三角関数の和を積に変換するとよいでしょう。公式の暗記はお勧めしません!公式を作って当てはめる方法もありますが,公式を作るのであれば,その手順で計算してしまえばよいです。

式(2)は,このタイプの問題としては基本的なアプローチです。2つの角の和があるときは,$${A+B=\pi-C}$$として文字を1つ減らす変形がポイントです。
式(3)は第1項から$${\sin\frac{\pi-C}{2}=\cos\frac{C}{2}}$$と$${\cos\frac{C}{2}}$$が現れるので,第2項も2倍角の公式から$${\sin C=2\sin\frac{C}{2}\cos\frac{C}{2}}$$として$${\cos\frac{C}{2}}$$を作り出しました。
導きたい式と比較すると,式(4)の()の中に$${C}$$は必要ないから,$${C=\pi-(A+B)}$$を代入して$${C}$$を消去しています。
最後の式(6)は加法定理で展開してしまえばおしまいです。

(2)もアプローチは(1)と同じです。考える順番まで同じですね。それでも決して容易ではありません。1式ずつよく確認しておきましょう。

結論も興味深い問題ですね。三角関数の式変形も十分に慣れておく必要があります。何度も繰り返し解いておきたい問題ですね!
