
第18回 これだけ!微分(微分積分)
前回は極限の不定形についてその求め方を学びました。
今回は微分について学んでいきます。高校範囲のおさらいなので駆け抜けていきましょう!
1.あなたはこの関数を描けるか
問題です。以下の関数の形を"正確に"描いてみてください。(ここでいう"正確に"とは極値と変曲点を明確にすることを指します。)
$$
f(x)=\frac{e^x}{x^3}
$$
どうですか?描けましたか?
"正確に"描けた方、あなたは微分を十分に理解してますので、この回は飛ばしてもらっても構いません。
なんのこっちゃという方、安心してください、この先を読めばばっちり描けるようになります。
2.正確に描くためには、そして微分とは
さて、関数の概形を"正確に"書くためには何が必要でしょうか?前の節に答えが書いてあります。それは、(微分を用いて)"極値"と"変曲点"を明確にすることです。では"極値"と"変曲点"とはなんでしょうか。そして微分とは何なのでしょうか?
(1)極値
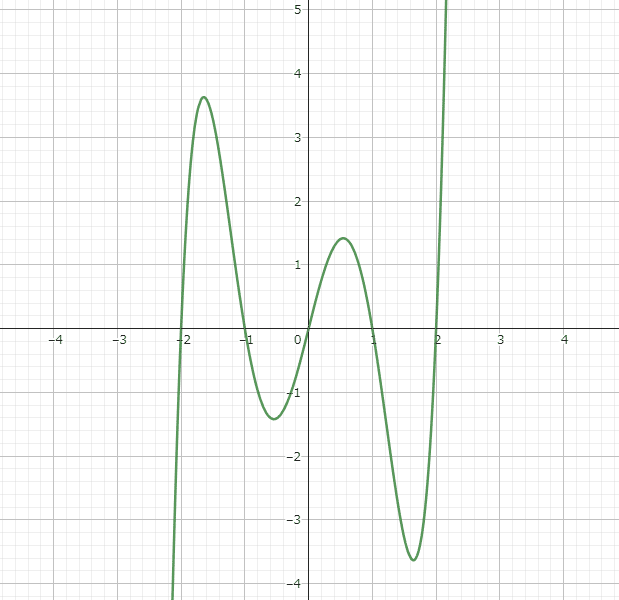
極値とはいわば"こぶ"の頂点です。下の図をご覧ください。こぶがいくつもあるのがわかるでしょうか?このこぶには必ず頂点がありますね。このこぶ、頂点における関数の値のことを極値といいます。そのこぶが上を向いているか(上に凸)、下を向いているか(下に凸)で頂点の呼び方が変わります。上に凸の時は頂点がこぶのなかで一番大きな値となるので極大値、下に凸の時は頂点がこぶのなかで一番小さな値となるので極小値と呼びます。
より数学的に表現をすれば、ある点が極値であるための必要十分条件は、関数の微分(傾き)が0であり、かつその点が変曲点ではないことです。
(2)変曲点
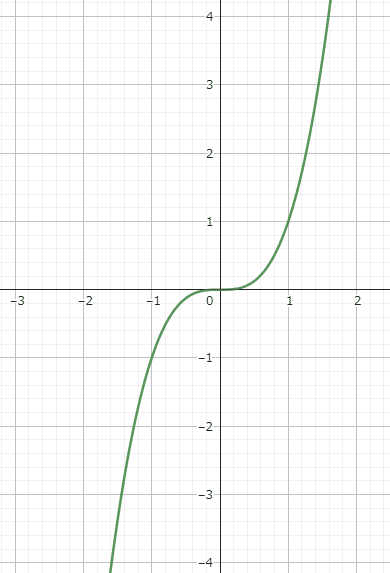
下の図をご覧ください。この関数、傾きは常に右肩上がりですね。しかしよく見ると傾き方が場所によって異なるのがわかるでしょうか。具体的には$${x}$$が負の場合は傾きがだんだん緩やかになっているのに対して、$${x}$$が正の場合は傾きがどんどん急になっていく傾向があります。そして$${x=0}$$を境に傾向がガラッと変わっていますね。このように関数の傾き方が変わる点のことを変曲点といいます。
より数学的に表現すれば、ある点が変曲点であるための必要十分条件は、その点を境に関数の二階微分(微分の微分、傾きの傾き)の正負が入れ替わることです。
(3)結局微分とは
関数を正確に描くためには極値と変曲点を求めればよく、その二点を求めるためには関数を微分、つまり傾きを求めればいいんだよと先ほど書きました。微分と聞くとなんだか身構えてしまいますが、微分とは端的に言えば関数の"傾き"を求めるための方法で、「関数がどんな感じで増減していってるのかな?」という傾向を把握するための手法なのです。それ以上でもそれ以下でもないです。まずはこの考え方から理解しておきましょう。
2.極値と変曲点を求めるためには
前の節から抜粋します。
「ある点が極値であるための必要十分条件は、関数の微分(傾き)が0であり、かつその点が変曲点ではないことです。」
「ある点が変曲点であるための必要十分条件は、その点を境に関数の二回微分(傾きの傾き)の正負が入れ替わることです。」
つまり、極値を求めるためには関数の傾き(微分)を求めればよく、変曲点を求めるためには関数の傾き(=微分した関数)の傾き(微分)を求める必要がありますね。じゃあ傾きを求めましょう!…でもどうやって?
(1)基本的な考え方
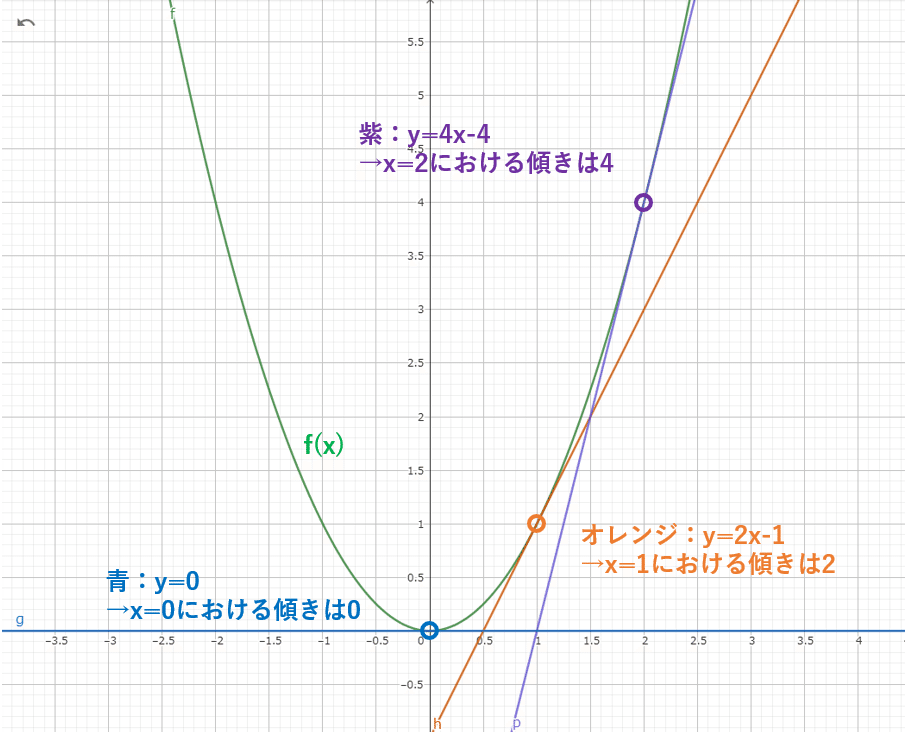
まず関数の傾きとは何か。関数の傾きとは関数のある点における接線(1次関数)の傾きです。下図のようなイメージですね。
いやそんなことを言われても接線の傾きなんて求められんし…と思ったら、こう考えてください。

上図のようにある点$${x}$$とその先の$${x+h}$$にある点を結んでみましょう。この線の傾きはどうなりますか?
$$
(傾き)=\frac{f(x+h)-f(x)}{(x+h)-x}
$$
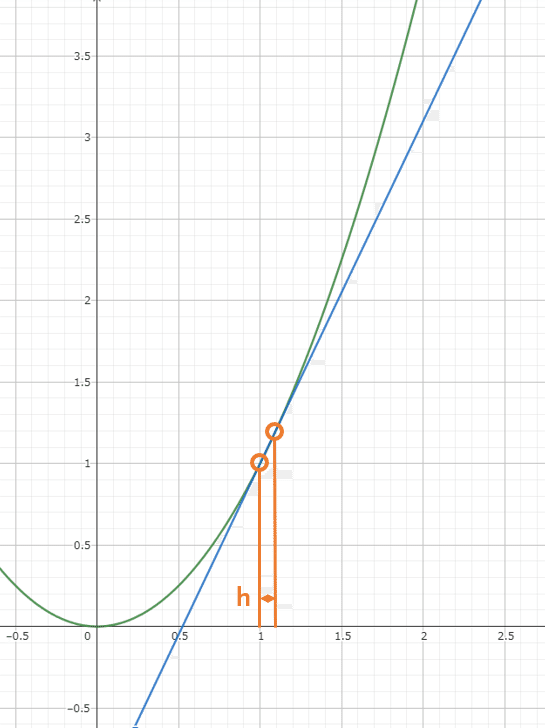
と書けます。この線分、何となく接線に近いようで違いますね。ではこの2点間の幅hを狭めていきましょう(頭の中で想像してみてください)。徐々に接線に近づいていくのが想像できますか?
ではhを限りなく0に近づけましょう(下図)。そしたらこの2点をつなぐ直線は、接線そのものに限りなく近いものになりますよね。
これが傾きを求めるための手順です。この手順を式にすると以下になります。
$$
f'(x)=\lim\limits_{h→0}\frac{f(x+h)-f(x)}{(x+h)-x}
$$
この$${f'(x)}$$を導関数といいます。ある$${x}$$における関数の傾きを示しています。導関数はその名の通り関数です。そうです、ある関数の傾きは関数で表せるのです。
つまりここまでをまとめると、
「関数がどんな形をしているのか知りたい!→そのためには関数の形を端的に示す極値と変曲点を求める必要がある→それらを求めるためには関数の傾きを求める必要がある→そのための方法として関数を微分しよう→微分するための手順は1にも2にも導関数を求めることだ」
こういう考え方をするわけです。
(2)代表的な微分公式
先ほど説明した導関数を用いれば、様々な関数を微分することができます。以下に代表的な公式を載せておくので、暇なら導関数を計算して公式を証明してみましょう。
$$
([関数])'=[微分後の関数]
$$
$$
(c)'=0 :cは定数
$$
$$
(x^{a})'=ax^{a-1}
$$
$$
(\sin{x})'=\cos{x}
$$
$$
(\cos{x})'=-\sin{x}
$$
$$
(\tan{x})'=\frac{1}{\cos^2{x}}
$$
$$
(a^{x})'=a^{x}\ln{a}
$$
$$
(\log\nolimits_a{x})'=\frac{1}{x\ln{a}}
$$
$$
(f(x)g(x))'=f'(x)g(x)+f(x)g'(x)
$$
$$
(\frac{f(x)}{g(x)})'=\frac{f'(x)g(x)-f(x)g'(x)}{g(x)^2}
$$
$$
{f(g(x))}'=f'(g(x))g'(x)
$$
3.実際に曲線を描いてみよう
冒頭に出てきたこいつ。もうあなたは概形を正確に描くことができます。一緒にやってみましょうか。
$$
f(x)=\frac{e^x}{x^3}
$$
まずは極値と変曲点を求めましょう。$${f(x)}$$を微分します。
$$
f'(x)=(\frac{e^x}{x^3})'=(\frac{1}{x^3})'e^{x}+\frac{1}{x^3}(e^{x})'
$$
$$
=\frac{-3x^2}{x^{6}}e^{x}+\frac{x^3}{x^{6}}e^{x}=\frac{x-3}{x^{4}}e^{x}
$$
ついでに$${f'(x)=0}$$となる$${x}$$を求めておきましょうか。
$$
f'(x)=\frac{x-3}{x^{4}}e^{x}=0
$$
上記を満たすxは、
$$
x=3
$$
ですね!
$${f'(x)}$$をさらにもう一回微分します($${f(x)}$$の二階微分)。
$$
f''(x)=\frac{x^{2}-6x+12}{x^{5}}e^{x}
$$
$${f''(x)=0}$$となる$${x}$$は存在しません。変曲点はありませんね。
そうそう忘れてはいけません。x=0の時に$${f(x),f'(x),f''(x)}$$は発散します。注意しましょう。
さて、必要な材料はそろいました。ここからどうするか。高校で習った内容を思い出してください。表を作るんでしたね。

この表に導関数の正負を記入します。そして極値、変曲点における関数の値を計算して書いておきます。

そして記入した情報から、関数がある区間でどんな形になるのかをまとめるんでしたね。

ここまで書けたらあとはグラフに書くだけです。表を見ながら線を描いていきましょう。
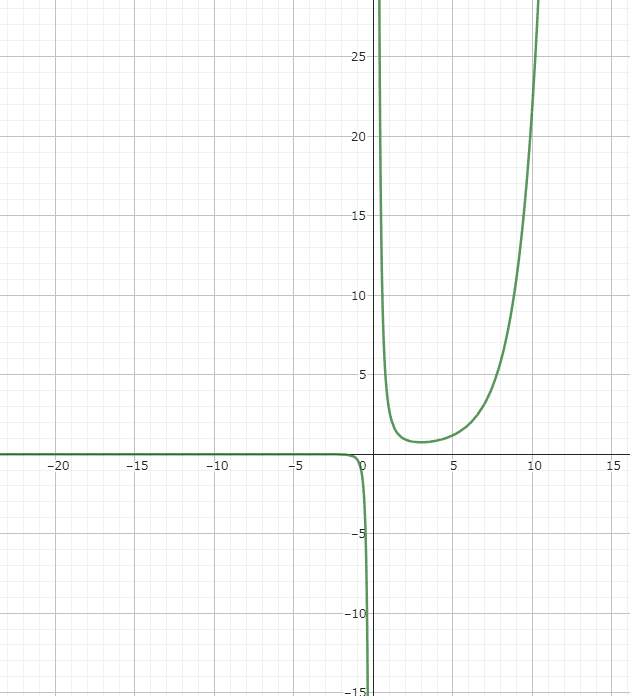
これで完成です!簡単ですね。
まとめ
今回は曲線の描き方を通して微分とは何かを解説しました。え、これだけ?と思う方もいるでしょうが、これだけです。これだけ理解できれば大学範囲の微分にも太刀打ちできます。しっかり理解しておきましょう!
次回はいったん微分からは離れ高校範囲の積分をおさらいします。
参考文献はこちら。ぜひ手に取って勉強してみてください。
