
『永遠に続く数』~憧れの素数を追い続ける私~リテラ探求学習研究レポート
人はなぜ素数に挑み続けるのでしょうか。
中3のMさんは、8歳の頃から素数に憧れ、その謎を追い続けています。
今回は、古代ギリシアの科学者、エラトステネスが考案したとされる、素数を発見するためのアルゴリズム「エラトステネスの篩」に挑戦しました。
この研究をしたのは新中3年生のM・Hさんです。
■プレゼンテーション動画
■リテラの先生からのコメント
フィボナッチ数列の研究や糸かけ曼荼羅のワークショップなど、これまで教室で取り組んできたことがつながって今回の研究になったと思うと、とても嬉しい気持ちになります。
素数はまだまだ分からないことがたくさんあります。
永遠に終わらない素数のように、Mさんの興味も広がっていくことを願っています。

■テキスト資料
みなさん、今年、アメリカで大発生する数学と自然の神秘の象徴をご存じですか?
その象徴とは「素数ゼミ」です。

まずは素数ゼミについて簡単に調査してみましょう。
素数ゼミは通常、アメリカの東部や南部に生息しています。

そして、今年、素数ゼミは221年ぶりに1兆匹の大量発生をむかえます。
なぜ221年ぶりなのか、それはセミが土の中で過ごす時間に関係しています
。
このセミたちは発生する年こそ違えど、13年または17年を周期に幼虫として過ごしています。
他のセミの羽化と重ならないよう、素数である13年や17年という周期になっていると言われています。
しかし、今年は、13年と17年の最小公倍数である221年目にあたるため、大量発生が起こってしまうのです。

では、素数とはなんでしょうか。
定義に従うと「2以上の整数のうち、1と自分自身でしか割り切ることのできない数」を、素数と呼びます。

たとえば143や137の場合で考えてみましょう。
143は11と13で割り切ることができます。
だから、素数ではありません。
しかし、137は1か137でしか割り切ることができません。
そのため、137は素数であるといえます。

このような素数を、連続する数の中から抜き出す方法を、たくさんの数学者たちが考えています。
その中でも、もっとも有名と言えるのが「エラトステネスのふるい」です。古代ギリシアの学者であるエラトステネスが考えたこの方法は、簡単に言えば「素数でないものを無くしていく消去法」です。
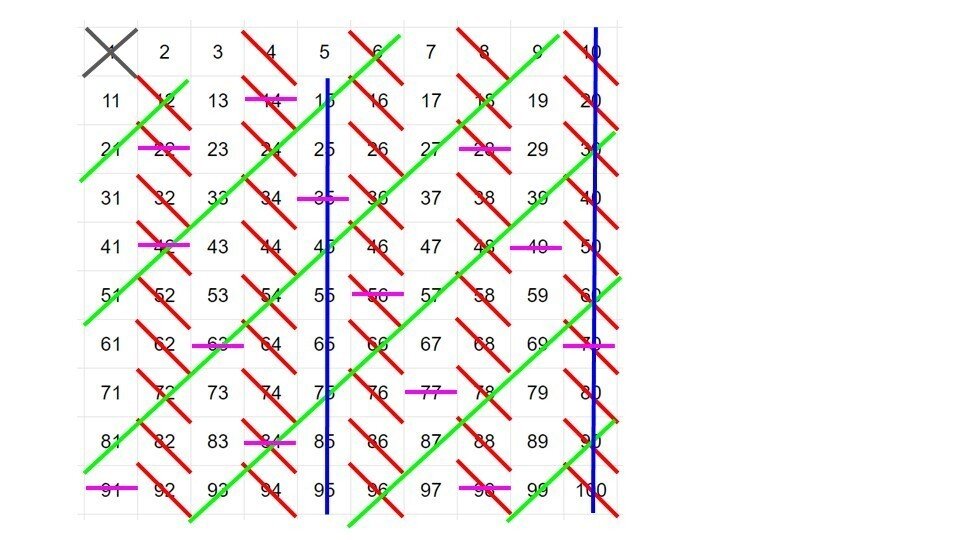
それでは、実際に、エラトステネスのふるいを1~100までの数でやってみましょう。
まずは1~100までの数を10ごとに区切った表を書きます。

次に、素数というのは「2以上の整数」と定義されているので、1を消します。

次に、2の倍数を消します。この時、2は、1と自分自身である2でしか割れない数、すなわち素数なので、消しません。

そして、3の倍数も消します。
3は、2と同じ理由で消しません。

5の倍数も消します。
5も2や3と同じ理由で消しません。

最後に7を消します。
7も、2、3、5と同じ理由で消しません。

11から先は、1~100までの数の場合、既に他の数の倍数として消されているので、これ以上消す必要はありません。

そして、残った25個の数が、1から100の間にある素数になります。
本では、100までの数しか表が乗っておらず、また、ネット上には10で区切った表が無かったため、今回、私は、1~1000までの数を、10ずつで区切った表を作ってみました。

始めは500までの予定だったのですが、勢いに任せて作図していたら、1000まで増えていました。
作るのに時間がかかり、途中で増やしたことをすごく後悔しました。
こちらが、完成した表です。


この作図だけでも大量の時間を使ってしまいましたが、ここから内容を更に膨らませていきます。

私は、この図から、なにか規則性を読み取ることができないか、探してみました。
そこで、一の位が5の数よりも左にある数と右にある数の中で、素数がいくつずつあるのか数えてみました。
結果はこの表のとおりになりました。100ずつに区切って細かく数えてみましたが、左と右の素数の数はあまり変わりません。1~500までの数の中での素数は、右のほうが左よりも一つ多く、501~1000までの数の中でも、素数は右のほうが左よりも一つ多かったので、1000から先の数も、500ずつで区切って調べたくなりました。

しかし、研究に費やせる時間の関係で調べられなかったので、次回までには調べたいです。
次に、100ずつ区切った数の中に、素数はどれくらい含まれているのかを数え、表とグラフを作成しました。
1~100と、101~200までに含まれている素数の数が圧倒的に多く、そこから先は、少なくなっていくように見えます。

しかし、1000までしか検証していないと、「少なくなっている」と言い切るには証拠が弱すぎるため、2000まで、範囲を拡大して調べました。
素数の検証としては、まだまだ証拠として弱いのですが、先程よりは傾向が見えやすくなる、はずです。
やはり、数の値が増えていくにつれて、素数の出現頻度は減っていく傾向があるように見えます。

なぜ、このように見えるのでしょうか。
皆さん、エラトステネスのふるいをやってみたときのことを、思い出してみて下さい。
2や3、5といった素数が見つかるたび、その倍数を消していきました。
それと同じように、新たな素数が見つかった時は、その素数の倍数も消えていきます。
つまり、数が大きくなるにつれて、今まで出てきた素数の倍数も消えていくので、素数になれない数の割合が増えていきます。
よって、大きな数になるほど、素数の出現頻度は小さくなっていくのです。
それでも、素数には「終わり」が存在しません。
これは、既に数学で証明されています。
しかし、素数が出現する規則性や、素数が二つおきに出現する「双子素数」は無限にあるのか、といった疑問は、いまだ未解決となっています。
素数はそうした未解決問題を、数多く秘めています。

そして、そんな素数の謎を追うことはとても大変だと、今回の研究を通して感じました。
人はなぜ、とても大変な素数に挑み続けているのでしょう。
私は、8歳の時、リテラの研究でフィボナッチ数列について調べたとき、訪れた数学の体験型ミュージアムで素数に触れ、テレビで「最大の素数が更新された」という内容のニュースを見ました。
9歳の時には、リテラで糸掛け曼荼羅を作成し、素数に興味を持ちました。研究のために素数ゼミを調べましたが、当時の自分にはあまりにも難しい内容だったので、発表は断念したことを覚えています。

そして、今年、先生と研究のテーマを話し合っていた時、偶然思い出したのが素数でした。
自分にとってリベンジとなる素数の研究は、理解できるようになった定義も、まだ分からないような数式も、調べるだけで面白かったです。
しかし、まだ、理解したい定義や書いてみたい数、試してみたい考え方も、知りたいことも、たくさんあります。
数学者たちも、同じような素数の魅力に取り憑かれてしまったのかもしれません。
私も、来年の研究で、続きを発表しようと思います。
それまでに、どれだけの知識を得ることができるのか、楽しみです。
これで発表を終わります。
聞いてくださって、ありがとうございました。
■研究の振り返り
◇これはどのような作品ですか?
素数について自分でも検証したいことに挑戦してみた作品です。
◇どうしてこの作品をつくりたかったのですか?
頭に「素数」という単語が浮かんだからです。
◇作品づくりで楽しかったことは何ですか?
全てが楽しかったです。
◇作品づくりで難しかったことは何ですか?
(難しかったというより、大変だった、ですが)エラトステネスのふるいを1000までやってみたことです。
◇作品作りを通して学んだことは何ですか?
素数に関する様々な法則や、作品を作る途中に出てきた言葉や単位などを学びました。
◇次に活かしたいことや、気をつけたいことはありますか?
仮説をたてることです。 疑問→仮説→検証→結果→考察の流れを忘れずに取り組みたいです。
◇来年、研究したいことはありますか?
今回の研究の続きを研究したいです。
◇この作品を読んでくれた人に一言
「素数」や「数学」、大きく言うと「学問」は面白いと思いませんか?
この研究をしたのは

