
ジャンル別ゲームの作り方 (2Dアクション・2Dシューティング)
今回はゲームジャンル別に、そのジャンルを代表する要素の作り方を紹介したいと思います。
◾️シューティングゲーム

シューティングゲームの基本的な面白さは、おおよそ以下の通りになるかなと思います。
* 動き回る敵を狙って倒すのが面白い
* 自機がパワーアップして敵を蹴散らすのが楽しい。もしくはパターンを覚えて効率よく敵を倒す
* 大量の敵弾をくぐり抜けた時のうまく操作した感、達成感
こういった面白さを実現するために、シューティングを作る場合、たいていは以下のステップでゲームを作ることになるかと思います。
(※1つの例です)
1. 自機の実装: 自機の表示・操作・画面からはみ出ないようにする
2. 自弾の実装: 自機から弾を発射する。弾が画面外に出たら消える
3. 敵の実装: 敵の表示。自機や自弾と衝突したらお互いに消える
4. 敵弾の実装: 自機に敵弾が当たったらゲームオーバー
5. アイテムの実装: アイテムを取るほど、弾をたくさん発射できるようにする
6. 敵の生成の実装: 敵を生成する処理を作る。まずは時間経過に伴い、次々と出現する処理で良い
7. ゲームクリア: 一定数敵を倒したらゲームクリアとする
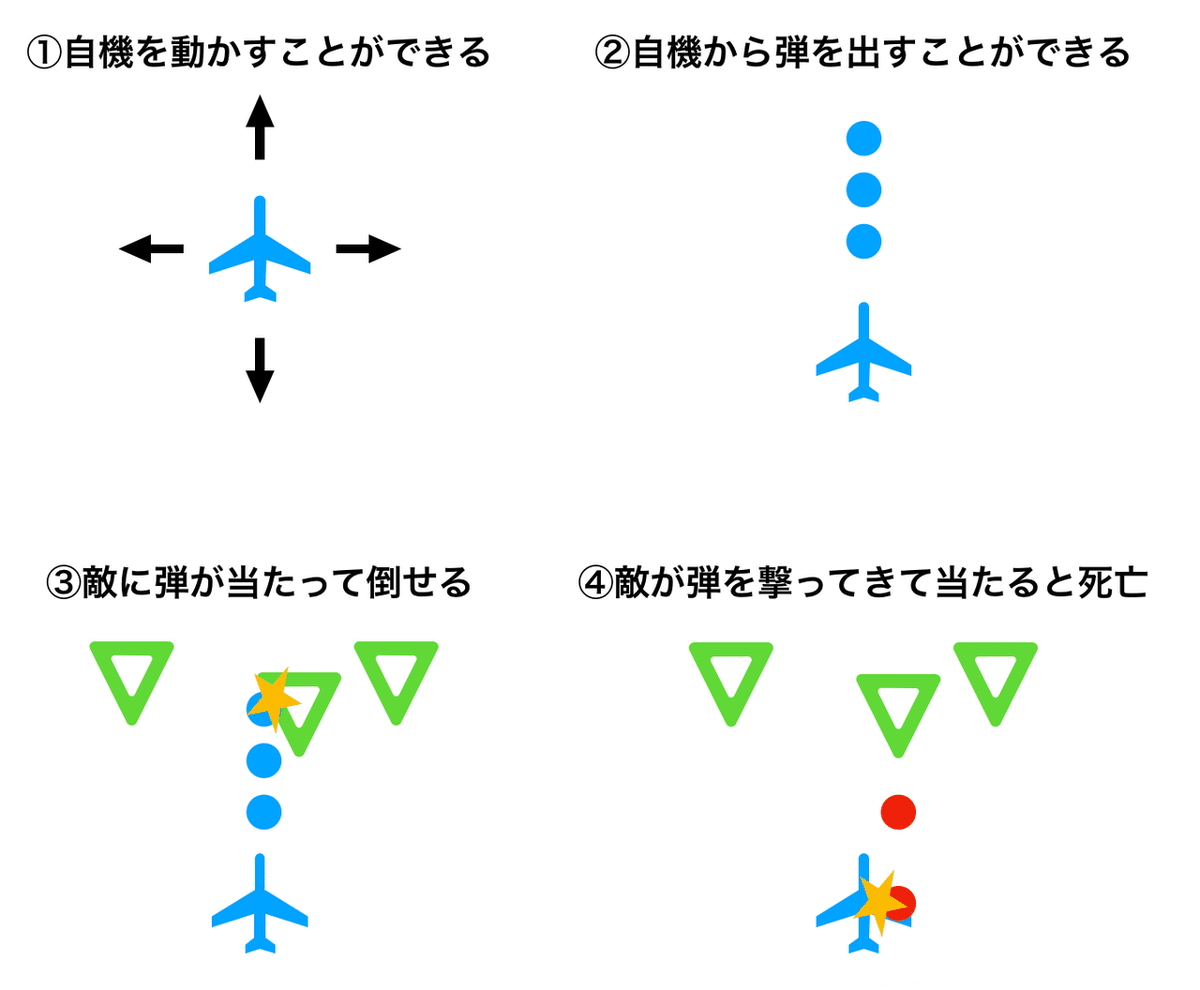
自機の移動をどのようにするか、攻撃の操作方法をどうするか、どんなパワーアップをするかはゲーム内容によりますが、基本はこのような流れとなります。
シューティングを作る場合、当たり判定を矩形(四角形)または円のどちらかにするかで、作りが少し変わってきますが、基本的に円を採用した方が、遊んだときの印象が良くなります。理由は矩形だと角に弾が当たってしまい、敵弾が避けにくくなるためです。ただ、敵は事情が異なって、デザインによりますが、例えば巨大である敵の当たり判定は、矩形である方が図形を組み合わせやすかったりするので、最終的には両方できた方がより良いです。
それと、弾の発射の速度は、入力を「極座標系」で扱うと、ゲームバランスが取りやすいです。

このような 直交座標系のX / Y で速度を扱うのではなく、

「角度」と「半径 (速さ)」で移動量を表現できる極座標系を使えるようにすると、直感的で扱いやすい値となり、ゲームバランスの調整がしやすくなります。
例えば、45度に10の速さで発射する、とすれば、斜め右上に10の速さで弾が発射されることになります。

「ちょっと弾が速すぎるな……」などと思って速度を遅くしたい場合は、速さ(半径)だけを小さくすれば遅くできます。
これを直交座標系でやろうとすると、X方向の値とY方向の値を細かく調整する必要があり、かなり時間がかかってしまい大変です。
また、3方向に弾を撃つ3WAY弾(または扇弾) という、シューティングではお約束の計算も、
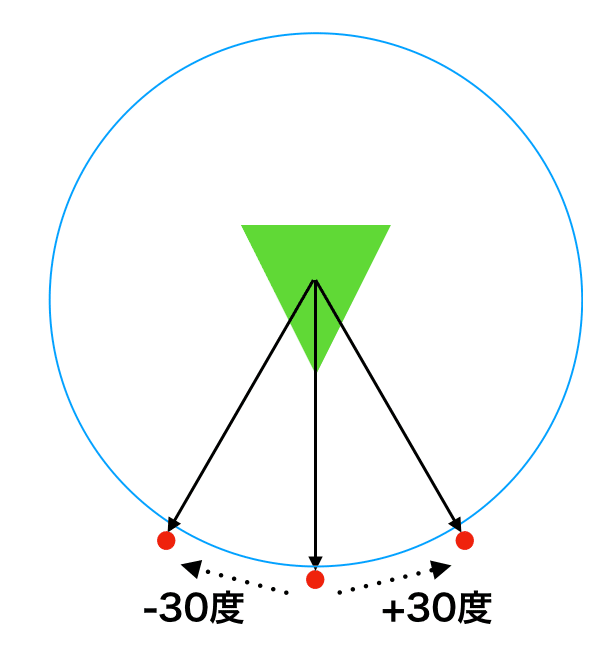
基準となる方向から、例えば±30度という計算で発射することが可能になります。また、「簡単に弾のスキマを避けられるので、もう少し弾と弾の間隔を小さくしたい」と思ったら、「30度」を「20度」に変える、という調整で簡単にできます。
プログラムの実装方法としては、以下のように三角関数(cos/sin)を使って極座標系から、直行座標系(XY軸)に変換します。
float rad = radians(45); // 度からラジアンに変換
float speed = 10; // 速さ
float vx = speed * cos(rad); // X軸の速度を計算
float vy = speed * -sin(rad); // Y軸の速度を計算また、狙い撃ち弾の角度計算はatan2 という三角関数を使います。
たいていの言語であれば、以下の記述で狙い撃ち弾の角度が計算できます。
float dx = player.x - enemy.x; // プレイヤーへのX軸の方向
float dy = player.y - enemy.y; // プレイヤーへのY軸の方向
float rad = atan2(-dy, dx); // 方向を求める
float deg = degrees(rad); // ラジアンから角度に変換する
sin / cos / atan2 を使うのは数学的な理由があるのですが、ひとまずこの3つが使えれば、基本的なシューティングゲームは効率よく作れます。
興味があれば「三角関数」で調べて数学の知識を深めるのも良いと思います。
■トップビューのアクションゲーム

トップビューは上から見下ろした視点のゲームで、ファミコン時代によく見かけた、マス目状に地形が区切られたマップをプレイヤーが移動する、「ゼルダの伝説」のようなゲームを想定します。
こういったゲームを作る場合には、マップデータは2次元配列で用意します。
例えば、0を通路、1を壁として以下のようなデータを定義します。
// マップデータテーブル
int map[5][5] = {
{ 1,1,1,1,1 },
{ 1,0,0,1,1 },
{ 1,1,0,0,1 },
{ 1,0,0,0,1 },
{ 1,1,1,1,1 },
}
このデータは、以下のような地形(マップ)をイメージしたものです。
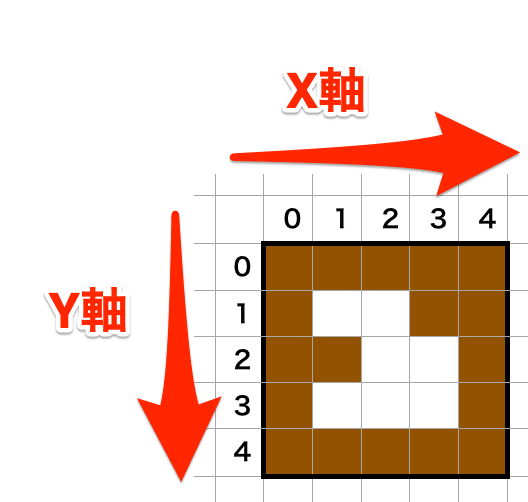
問題となるのが、マップデータ上の座標系と実際にゲーム画面に表示する座標系が異なることです。
例えば、マップの1つのマス目のサイズが幅x高さが 32x32 だった場合、
マップ上での (x, y) = (2, 3) にいるキャラクターの画面上での座標の計算は、
x = 2 * 32; // プレイヤーのX座標は、マス目座標Xとマスの幅をかけた 64
y = 3 * 32; // プレイヤーのY座標は、マス目座標Yとますの高さをかけた 96で求まり、(x, y) = (64, 96) となります。
プレイヤーがマップを移動する場合には、こういった計算を相互に行い、そこに壁があったら進めない、という判定が必要になります。
なので、「マップ座標系」か「ゲーム画面での座標系」のどちらでデータを扱っているのかを意識して作ることが大切となります。
ここではプログラム上にマップデータを定義しましたが、Tiled Map Editor のようなマップエディタで作成したデータを読み込むことができるようにすると、マップデータの作成が効率化できるようになります。
このようなスクリーン座標系とマップ座標系の扱いに慣れるには、以前に解説した一筆書きゲームを、まずは一度作って理解するのも良いかと思います。
あと、トップビューの衝突判定についてです。トップビューでは(後述するサイドビューでも)、「衝突した時の押し返し(衝突応答)」という重要な問題があります。

この問題の解決法として押さえておきたいのが、「X軸とY軸を分離して計算する」ということです。
斜め移動が存在することを前提としますが、斜め移動した後に衝突判定を行うと、壁へのめり込みが発生した場合、どちらに押し返すのか判定することが難しく、問題が起きることが多いです。具体的な問題としては、壁に沿って歩く「壁ズリ」を実装するのが難しくなります。
そのため、移動する前に、まずは「X軸方向に移動させてみて、めり込んだらめり込まない位置まで戻す」次に「Y軸方向に移動させてみて、めり込んだら押し戻す」という方法を使うと、たいていの衝突応答は問題なく処理できます。

図では、Y軸方向のみ押し返していますが、X軸移動で衝突があった場合はX軸方向に押し戻しをすることが必要となります。
なお、Unityのように物理エンジンで衝突応答を行う場合はこのような制御は不要ですが、物理エンジン特有の問題に注意する必要があります。
トップビューのアクションゲームでの最後の問題点は「敵のAI」です。壁がない場合は自由に動いて良いのですが、壁がある場合にそれを迂回してプレイヤーを追いかける処理が必要となります。これを経路探索といって、敵が行き止まりに入り込まないように正しい道を教える必要があります。
方法としては、A*アルゴリズムを使うことでたいていは解決できます。
サンプルコードは Unity ですが、C#の基本的な機能しか使っていないので、どの言語にも移植できると思います。
◾️サイドビューのアクションゲーム

サイドビューは横からキャラクターや地形を見た視点です。
代表的なゲームとしては「スーパーマリオ」や「ロックマン」などですね。最近はスマートフォン向けに、ジャンプアクションに主体をおいた「ラン&ジャンプ系」のゲームが人気です。
トップビューとの違いは重力が加わっただけで基本は同じです。しかし重力が加わったことで、ジャンプによるスリルのあるアクションが生まれやすいです。トップビューよりも重力の影響でプレイヤーの操作に制約が出るため、それを考慮したゲームデザインにする必要があります。
例えば、サイドビューのアクションゲームでは弾幕シューティングのように敵が大量の弾を撃ってくるゲームデザインは、避けるのが困難になり、あまり好ましくありません。
類型としては、ロックマンのように弾を撃って敵を倒しながら進むゲームとするのか、ソロモンの鍵のようにアクション要素がありつつも、ギミックを使ったパズル要素を含めるのか、もしくはメトロイドのように閉鎖空間を探索するのをメインにするのかによって、それぞれ遊び方の幅が変わってきます。
プログラム技術としては、重力が加わったことで厄介なギミックがいくつか必要となります。例えば「移動床」の実装はやや難しいです。

基本的な機能は、移動床の上に乗っていたら移動床の動きに合わせてプレイヤーも動かす、という方法で実装できますが、特殊な場面の対応が難しいです。
* 壁と移動床にプレイヤーが挟まれたらどうする?
* 移動床が地面をすり抜ける際に、プレイヤーが移動床に乗っていたらどうなる?
* 移動床同士が交差した場合、その上に乗っているプレイヤーはどうなる?
といった場面の衝突応答の解決は難しいため、「移動床に挟まれたら死亡する」「壁の近くには移動床を置かない」「移動床は地面と交差しないようにする」などの仕様や配置上の制約を加えて、問題を未然に防ぐのが楽で良いです。
「斜面の床」の実装は、X方向から衝突した際に上方向に押し出す、という衝突応答で実装できます。
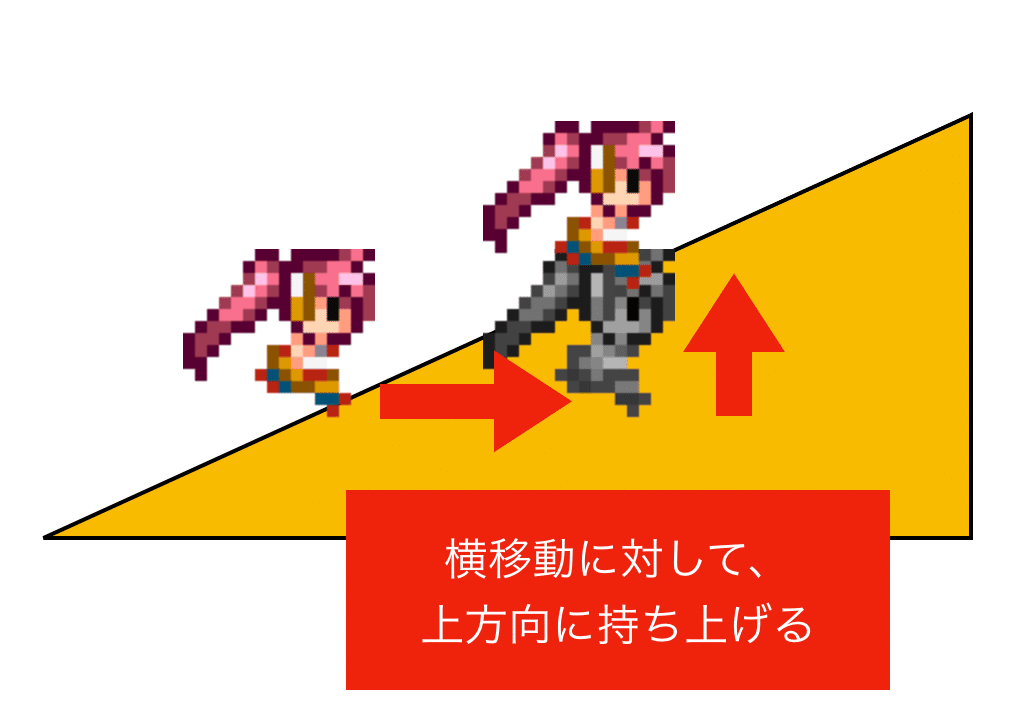
問題となるのが、上方向にどれだけ持ち上げるかですが、最初は45度の斜面だけにしてみるのが良いです。
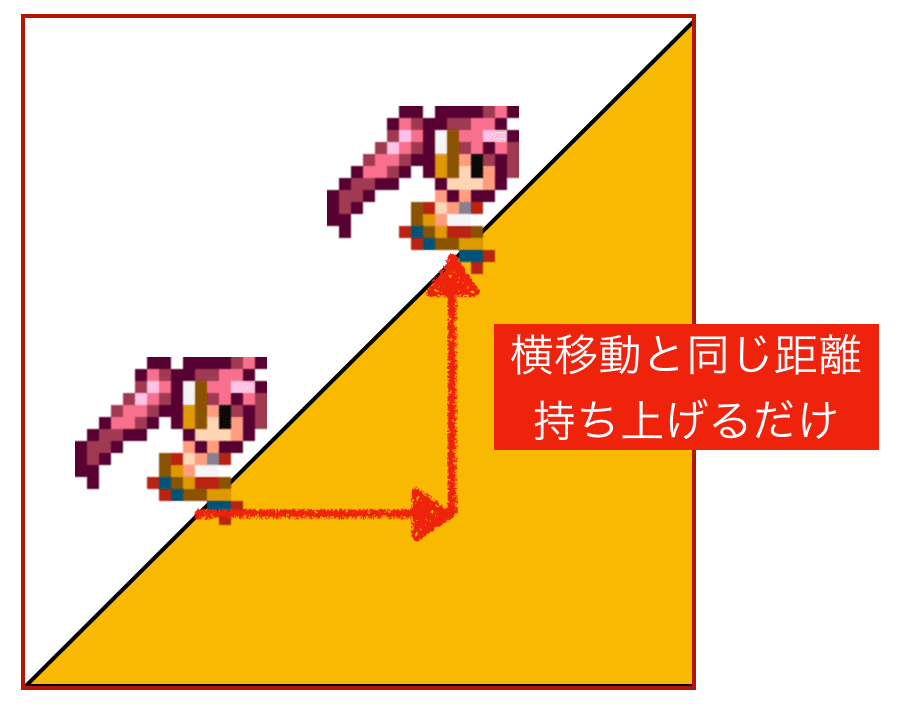
45度の斜面は、横幅と高さが同じ距離となるため、Y方向への持ち上げも同じ距離となって計算が簡単です。(正確には斜め移動なので、移動距離が√2 倍になってしまいますが、多くの場合は誤差として問題ないです)
45度だと傾斜がキツイのが気になる場合は、22.5度斜面を用意します。

45度斜面の半分の傾斜角度の地形を用意することで、X方向に移動に対して、Y方向は半分の値持ち上げるだけとなり、計算が楽です。
(なお、正確には底辺が2で高さが1となる直角三角形は atan2(1, 2) ≒ 26.565度なのですが、わかりやすく22.5度という用語を使うようにしました)
滑らかに斜面を繋ぎたい場合は、図のように22.5度斜面の後半マップチップを用意することで、スムーズに移動できるようにします。
さらなる問題は下り床です。そのまま横移動だけすると、ガクガク降りる動きとなります。これをスムーズに坂を下るようにするには、プレイヤーに斜面に接地しているフラグを保持するようにし、その場合の横移動は斜め下に移動する、というやや強引な方法で対処します。
その場合、下の移動距離を大きくしすぎると斜面の切れ目から落下した場合、ガクンとプレイヤーが沈みすぎてしまいます。この問題の解消方法としては、下り斜面の最後は平面の地形とつなぐルールで運用して回避するのが楽です。

また急な傾斜の下り坂は、ガクガク降りても仕方ない、と割り切るのも一つの解決法です。
あと、忘れられがちですが、すり抜け可能な「一方通行床」は実装コストが低くステージデザインの幅が広がるので、是非とも実装しておきたいギミックです。

実装方法は、上からの衝突のみ有効にする、です。つまり、左右からの衝突を判定せず、プレイヤーの移動が上昇中(Y方向の速さがマイナス)の場合は衝突判定をしない、という実装をします。また、一方通行床の上から降りられるようにするには、降りる操作(下+ジャンプなど)による落下開始後の一定フレームの間は衝突判定をしない、という方法で実装できます。
ハシゴの実装は、以下の制約で運用すると実装が楽です。

逆に難しくなるのが以下の仕様です。
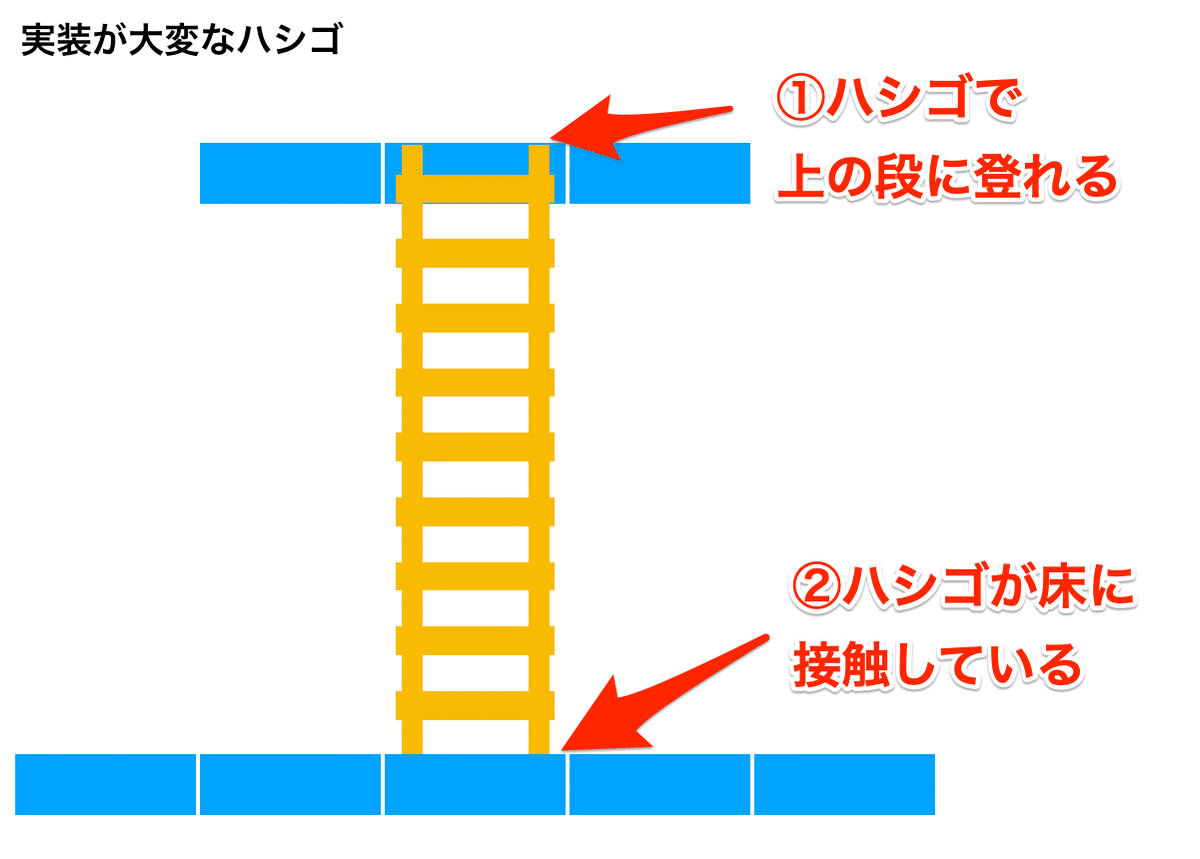
カプコン系のアクションゲームは、わりとここまでしっかり実装がされているので、自信があれば挑戦してみるのも良いでしょう。
■とりあえずここまで
書いていたら結構分量が多くなってしまったので、今回はとりあえずここまでとします。
アクションゲームとシューティングはお互いに相性が良いジャンルなので、「ロックマン」や「魂斗羅」のようにシューティング要素強めのアクションゲームといった組み合わせで何か作ってみるのもありかもしれません。
あと、アクションゲームはパズル要素(スイッチで扉が開くなど)と相性が良いので、尺稼ぎ……ではなくて遊びの幅を広げるためにパズル要素を入れるのも悪くないと思います。
■補足: 当たり判定について
特に説明をしなかったのですが、アクションゲーム、シューティングゲームでは、当たり判定の実装が必須となります。
2Dゲームでは、矩形(四角形)や円、線分の3つの当たり判定を作ることができれば、おおよそ実装できるはずです。
それぞれについては、「矩形 当たり判定」「円 当たり判定」「線分 当たり判定」で検索するとわかりやすく説明されたサイトがたくさん出るので、ここでは説明を省略します。
◾️補足: ゲームオブジェクトの管理について
アクションゲームやシューティングゲームでは、大量のオブジェクトを管理する仕組みが必要となります。
方法としては、ゲームオブジェクトの座標と移動値、当たり判定のサイズ、描画情報を一つのクラスに定義して、それを配列またはリストで管理することで実装できます。
オブジェクト管理の実装方法についてまとめました。
■関連するページ
今回の内容が難しかった場合は、初心者向けの簡単なゲームを作ってみるのも良いかもしれません。上記のページでは初心者向けのゲームを紹介しています。
