同値関係と両立する写像（５）

『引き起こす』に始まり、
　『同値関係と両立する写像（１）』の命題１、
　『同値関係と両立する写像（２）』の命題２
は、それぞれいくつかの演算の付帯された集合（これを一般に代数的構造（algebraic structure）、あるいは代数系（algebraic system）という）に拡張される。

前回の『同値関係と両立する写像（４）』でみた準同型定理は、『引き起こす』でみた命題（番号付けしていなかったので、ここでは「命題０」と番号を付けよう）の「代数系版」であることをみた。

今回はこの命題１、命題２に代数系の場合に相当する命題Ａ１、命題Ａ２をそれぞれ確かめよう。代数系の場合、写像は準同型写像に、同値関係は演算と両立する同値関係に対応する。

１．可換図式

まず整理のために命題０，１，２を図式にしておこう。

図式の説明になるが、まず真ん中に丸い矢印があるのは、図式の可換性ということを表現するときに使う。図式の可換性とは、任意の２つの対象（集合や代数系）の間を矢印に沿って進むとき、その進み方によらずに合成写像が一致することを意味する。可換である図式を可換図式という。次に矢印の上に付けているのは写像や準同型を表現している。実践の矢印は仮定した矢印で、それに対して破線の矢印は結論の矢印を表現する。つまり、破線の矢印は「引き起こされる」ということを意味する。また、記号「∃！」とあるのは、「一意的存在する」を表現する。「∃」は「存在する」を、「！」は「一意性」を意味する。

【命題０】

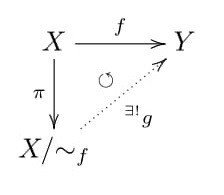
※同値関係～の下にｆがあるのは、「ｆで引き起こされた同値関係」という意味で用いている。

【命題１】

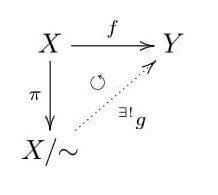
【命題２】

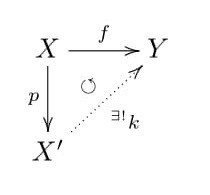
２．命題Ａ１

同じｎ項演算の間の準同型写像ｆ：(Ｘ，μ)→(Ｙ，ν)と、Ｘの上の同値関係～があり、演算μは同値関係～と両立するとする。このとき商集合Ｘ／～に演算μ’が引き起こされた。（『同値関係と両立する写像（３）』より）

同値関係～がｆと両立するための必要十分条件は、準同型写像
　ｇ：(Ｘ／～，μ’) → (Ｙ，ν)
で
　ｇ◦π＝ｆ
となるものが存在することである。

また、この同値な条件を満たすとき、準同型写像ｇは一意的である。

ここで、写像π：(Ｘ／～，μ’) → (Ｙ，ν)は自然な全射準同型とする：
　π(ｘ)＝[ｘ]
　　　＝｛ａ∈Ｘ｜ａ～ｘ｝
　（ｘ∈Ｘ）

３．命題Ａ１の証明

写像としてのｇの一意性は命題１でみたから一意性はよい。

【必要性の証明】
命題１により写像としてｇが定義されることはみた。これが準同型であることをみよう。

　　ｇ◦μ'([ｘ(1)]，･･･，[ｘ(n)])
　＝ｇ◦μ’◦(π×･･･×π)(ｘ(1)，･･･，ｘ(n))　　（∵直積写像の表示）
　＝ｇ◦π◦μ(ｘ(1)，･･･，ｘ(n))　　　　　　（∵πは準同型）
　＝ｆ◦μ(ｘ(1)，･･･，ｘ(n))　　　　　　　（∵ｇの定義）
　＝ν◦(ｆ×･･･×ｆ)(ｘ(1)，･･･，ｘ(n))　　　（∵ｆは準同型）
　＝ν◦(ｇ◦π×･･･×ｇ◦π)(ｘ(1)，･･･，ｘ(n))　（∵ｇの定義）
　＝ν◦(ｇ×･･･×ｇ)([ｘ(1)]，･･･，[ｘ(n)])　　（∵同値類で表示）
　　（ｘ(1)，･･･，ｘ(n)∈Ｘ）

よって、
　ｇ◦μ'＝ν◦(ｇ×･･･×ｇ)
より、ｇ：(Ｘ／～，μ’) → (Ｙ，ν)は準同型写像である。

【十分性の証明】
命題１によりｇを写像として適用すれば従う。■

４．命題Ａ２

集合Ｘ，Ｘ’，Ｙにそれぞれ同じｎ項演算μ，μ’，νが付帯されているとする。写像ｆ：(Ｘ，μ)→(Ｙ，ν)、および全射ｐ：(Ｘ，μ)→(Ｘ’，μ’)がそれぞれ準同型写像であるとする。

ｐの値で一致するようなＸの２元はｆの値でも一致する：
　ｐ(ｘ）＝ｐ(ｙ)　⇒　ｆ(ｘ）＝ｆ(ｙ)
　（ｘ，ｙ∈Ｘ）
ための必要十分条件は、準同型写像
　ｋ：(Ｘ’，μ’)→(Ｙ，ν)
で
　ｋ◦ｐ＝ｆ
となるものが存在することである。

また、この同値な条件を満たすとき、準同型写像ｋは一意的である。

５．命題Ａ２の証明

写像としてのｋの一意性は命題２でみたから一意性はよい。

【必要性の証明】
命題２により写像としてｇが定義されることはみた。これが準同型であることをみよう。

ｘ’(1)，･･･，ｘ’(n)∈Ｘ’を任意に取る。ｐ：Ｘ→Ｘ’の全射性より

　ｐ(ｘ(ｉ))＝ｘ’(ｉ)
となるｘ(ｉ)∈Ｘが各ｉ＝１，･･･，ｎについて存在する。このとき、

　　ｋ◦μ'(ｘ’(1)，･･･，ｘ’(n))
　＝ｋ◦μ’( ｐ(ｘ(1))，･･･，ｐ(ｘ(n)) )　　　　（∵ｐは全射）
　＝ｋ◦μ’◦( ｐ×･･･×ｐ)(ｘ(1)，･･･，ｘ(n) )　　（∵直積写像の表示）
　＝ｋ◦ｐ◦μ(ｘ(1)，･･･，ｘ(n) )　　　　　　　（∵ｐは準同型）
　＝ｆ◦μ(ｘ(1)，･･･，ｘ(n) )　　　　　　　　（∵ｋの定義）
　＝ν◦(ｆ×･･･×ｆ)(ｘ(1)，･･･，ｘ(n) )　　　　（∵ｆは準同型）
　＝ν◦(ｋ◦ｐ×･･･×ｋ◦ｐ)(ｘ(1)，･･･，ｘ(n) )　（∵ｋの定義）
　＝ν◦(ｋ×･･･×ｋ)(ｐ(ｘ(1))，･･･，ｐ(ｘ(n)) )　（∵ｐの値で表示）
　＝ν◦(ｋ×･･･×ｋ)(ｘ’(1)，･･･，ｘ’(n))　　　　（∵もとの元で表示）

よって、
　ｋ◦μ'＝ν◦(ｋ×･･･×ｋ)
より、ｋ：(Ｘ’，μ’)→(Ｙ，ν)は準同型写像である。

【十分性の証明】
命題２によりｋを写像として適用すれば従う。■

６．まとめ

集合に対する命題０，命題１，命題２は、代数系に対する準同型定理、命題A１、命題A２がそれぞれ同一の可換図式に対応することをみた。