
GeoGebraでベクトル場を描画する
ミケ:最近ベクトル解析の勉強をしているけど、いまいちイメージができないなぁ。
ミケ:手書きのグラフでもわからなくはないけど、複雑な関数は書けないしなぁ。
ミケ:…そうだ!こういう時こそGeoGebraじゃん!
ミケ:よーし、さっそく使ってみよう!
どうやら今回はベクトル場を描画していくようです。
ベクトルを描画する
まずは単にベクトルだけを描画することを考えてみよう。
ベクトルをつくるコマンドはVector()だから、この引数に「点」を入力していこう。「点」だから( )で囲むのを忘れないでね。
試しに(3,4)と入力すると…。

これは点(3,4)の位置ベクトルになるんだね。
また、Vector()の引数には(開始点、終了点)というものがあるから、これを使って(-2,2)から(-5,5)に向かうベクトルを書いてみると…。
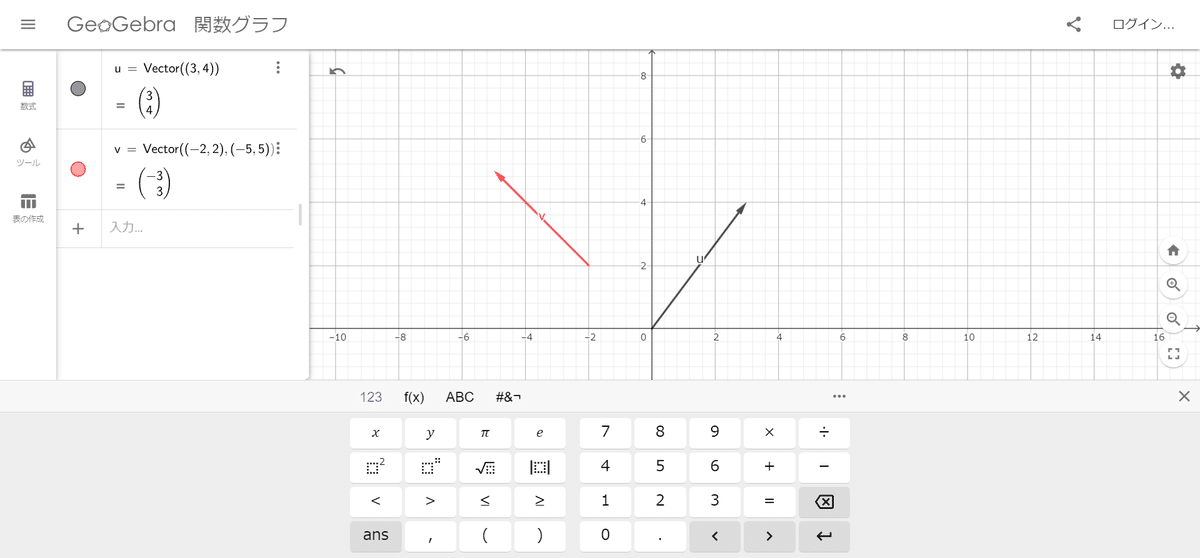
このように始点と終点をしてベクトルを書くこともできるよ!
ベクトル場を描画する
じゃあ本題のベクトル場を描画してみよう!
…としたいところなんだけど、残念なことにGeoGebraにベクトル場を描画するコマンドは用意されていないんだ。
だけど疑似的にベクトル場を描画する方法はあるから今からそれを使っていこう!
具体的にはSequence()コマンドを使っていくよ!これは簡単に言えば「ある具体的な範囲が与えられた変数を用いた値のリストをつくる」コマンドだ!
例えば、
//(式,変数,開始値,終了値,増分)
Sequence(2^(k),k,0,5,1) => {1,2,4,8,16,32}という風になる!これは「$${2^k}$$の$${k}$$を0から5まで1ずつ代入した値のリスト」を作っているんだね。
これを使えばx,y成分の値をそれぞれ変化させたベクトルのリストを作ることができる。つまりベクトル場が描画できるんだね。
じゃあベクトル場$${\mathbf{a}(x,y)=[f(x,y),g(x,y)]}$$を描画していくわけだけど、あらかじめ$${f,g}$$で関数を定義しておくと便利かもね!
今回は$${f=-y,g=x}$$と定義しておくよ。

こんな感じでSequence()の二重ループで(s,t)を[-5,5]の間に1ずつ変化させているよ!
このとき(s,t)ではなく(x,y)を文字として使うとうまくいかないから注意してね。
このベクトル場を$${\mathbf{a}=[-y,x,0]}$$って考えると$${\mathrm{rot}\mathbf{a}=[0,0,2]}$$なので、回転しているはずなんだけど数式だけだと意味がつかみずらいよね。
でもこうやってグラフで書いてみるとすぐに意味が分かるから便利だね~。
終わりに
ミケ:いやー、すごいなGeoGebra。まさかベクトル場まで描画できちゃうなんて。
ミケ:いや一番すごいのはこれが無料ってところか…。ありがたや~~。
ミケ:よーし、これでベクトル場がいつでも見れるようになったからどんどんグラフを書いていくぞー!
誤字脱字や間違い、質問や感想等は遠慮なくどうぞ!
ーミケー
