
フォースプレートによる床反力計測#4 〜身体側からみた床反力の物理的意味〜
前章までに,フォースプレートから見た床反力の物理的意味について述べた.ここから,身体側から見た床反力の物理的意味について述べていきたい.
1.フォースプレートで計測できること
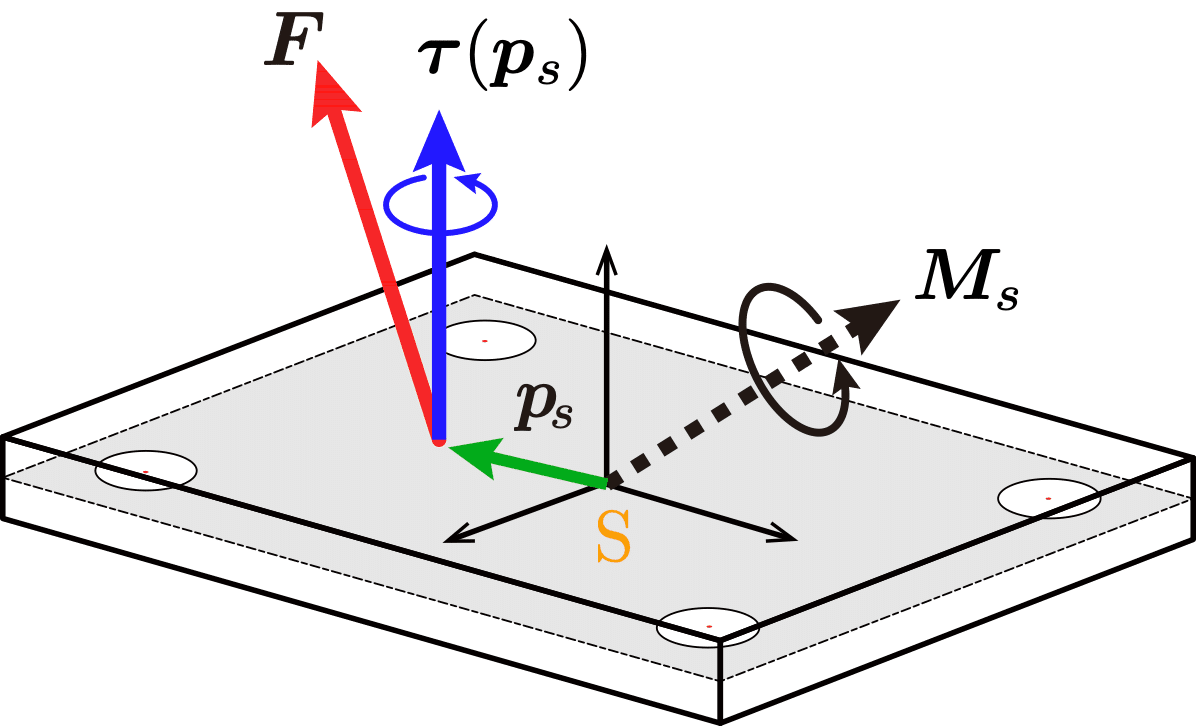
フォースプレートには4つの力覚センサが硬いプレートの下に埋め込まれ,その4つのセンサで
床反力$${\bm{F}}$$
を計測する.さらにセンサの位置などの情報から
フォースプレート座標系$${\text{S}}$$まわりの力のモーメント$${\bm{M}_s}$$
を計算して出力する.力学計算を行うためには,この床反力$${\bm{F}}$$と力のモーメント$${\bm{M}_s}$$と,フォースプレート座標系$${\text{S}}$$の位置情報が必要となる.
この力のモーメント$${\bm{M}_s}$$は,平行軸の定理を用いて,水平軸回りの力のモーメントがバランスし0となる圧力中心回りのモーメントに変換し
$$
\bm{M}_s = \bm{\tau}(\bm{p}_s)+ \bm{p}_s \times \bm{F}
$$
と置き換えることで,
COP(圧力中心)$${\bm{p}_s}$$
摩擦モーメント$${\bm{\tau}(\bm{p}_s)}$$
を計算することができた.このCOPは鉛直方向の床反力がバランスする重心点としての意味を持ち,COPでは鉛直方向の摩擦モーメント$${\bm{\tau}(\bm{p}_s)}$$だけが作用する.
いずれにせよ,これらはフォースプレート側の力学で定まる物理量である.
2.床反力を拘束する身体の力学
フォースプレートに作用する力は,もともと身体が発揮することによって発生する力である.そこで,フォースプレート側の立場ではなく,身体の力学から床反力やCOPなどが身体運動によってどのように定まるか考えていきたい.ただし,考え方はフォースプレートの力学と基本的に同じである.
静止してフォースプレートの上に立てば,フォースプレートの計測値には体重が反映されるが,体重に加えてさらに運動によって床反力に変化を及ぼす.その力学をここで考える.

身体は複数の部位(たとえば,手や大腿などを指す)が関節で接続している構造とし,さらに身体の各部位が剛体であると仮定すると,$${i}$$番目の部位の運動方程式は
$$
m_i \ddot{\bm{x}}_{gi} = m_i \bm{g} + \bm{f}_i
$$
となる.ここで,$${m_i}$$は部位$${i}$$の質量,$${\bm{x}_{gi}}$$は部位$${i}$$の重心の位置ベクトル,$${\bm{g}}$$は重力加速度ベクトル,$${\bm{f}_i}$$は部位$${i}$$に作用する力である.力は関節を通して複数作用することがあるが,ここでは便宜的に一つだけ記述している.
左辺は,身体部位$${i}$$の質量と加速度の積で,これは部位$${i}$$の慣性力に相当し,「部位$${i}$$の運動によって生じる(見かけの)力」を表している.
また,関節に作用する力の場合,$${\bm{f}_i}$$は関節を通して,別の部位に反作用の力$${-\bm{f}_i}$$として作用するので,全身で関節に作用する力を加算するとこれらは全て消去される.このような性質を持つ力は内力と呼ばれるが,内力については
を参照されたい.
さて,床反力を拘束する全身の運動方程式は,これらを全て加算し
$$
\sum_i^n m_i \ddot{\bm{x}}_{gi} = \sum_i^n m_i \bm{g} + \sum_i^n \bm{f}_i
$$
となる.左辺は全身の慣性力の和であるが,全身の身体重心を下記のように
$$
\bm{X}_{G} = \frac{\sum_i^nm_i \bm{x}_{gi}}{\sum_i^n m_i}
$$
定義し,
$$
\sum_i^n m_i \bm{x}_{gi} = \sum_i^n m_i \frac{\sum_i^nm_i \bm{x}_{gi}}{\sum_i^n m_i} = M \bm{X}_G \\ \sum_i^n m_i \ddot{\bm{x}}_{gi} = \sum_i^n m_i \frac{\sum_i^nm_i \ddot{\bm{x}}_{gi}}{\sum_i^n m_i} = M\ddot{ \bm{X}}_G
$$
を得る.ここで,$${M=\sum m_i}$$は全身の質量である.つまり,左辺の「各部位の慣性力の総和」は「体重と身体重心の加速度で表現した慣性力」に置き換えられる.
右辺の身体に作用する力は関節に作用する力が全て消えてしまうが,他に唯一床から外力$${\bm{F}}$$だけが作用するとすると,以上から,全身の運動方程式は
$$
M \ddot{\bm{X}}_{G} = M\bm{g} + \bm{F}
$$
となる.
このように全身の力学(ダイナミクス)は加算することで,身体重心$${\bm{X}_G}$$と床反力$${\bm{F}}$$で記述でき,床反力は
$$
\bm{F} = M (\ddot{\bm{X}}_{G} - \bm{g})
$$

と書くことができる.実際には筋肉や関節の粘性抵抗のエネルギー消散などを含むため,これらは完全に一致しないが,床反力は重心の加速度と重力で記述できることを示している.
静止して,身体重心$${\bm{X}_G}$$の加速度が0なら,体重と等しくなり,もし運動すれば,さらに身体重心の加速度$${\ddot{\bm{X}}_G}$$に比例して変動する.
これらの式が意味することは,「全身の並進のダイナミクスにおいて身体と接している床反力だけが唯一の外力」で,身体にとって唯一のエネルギー源は床反力であることを示している.
そして,その動力源を定める力学(ダイナミクス)は身体重心の加速度$${\ddot{\bm{X}}_{G}}$$が支配している.つまり,大きな外力を得るためには,身体重心の動かし方(加速度)が強く支配していることを示している.
3.身体重心の力学
身体重心は定義
$$
\bm{X}_G =\sum_i^n \bm{x}_{gi} = \frac{\sum_i^nm_i \bm{x}_{gi}}{M}
$$
から「各部位の質量で重み付けされた加速度」を意味している.また,前節では床反力を支配するのが身体重心の加速度であることを述べた.すると,大きな身体重心の加速度,すなわち大きな床反力を得るためには,身体で質量が大きい部位が体幹回りや下肢にあるので,体幹回りや下肢の加速度を大きくすることが重要となる.
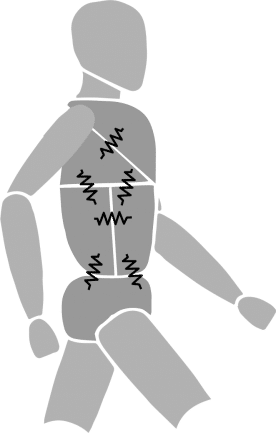
また,目的とは反対方向の加速度が発生すると力が相殺されてしまうので,どの部位も同じ方向の加速度が生じるように,身体を一体化させることが重要といえる.したがって,スポーツのように速く走ったり移動する場合に,大きな床反力を得るためには,身体の中で質量の大きい体幹回りや下肢の部分が一体化し,その加速度がおおよそ同じ方向を向いていることが重要であることが推察される.もし身体の各部位がバラバラに動いていては,力が相殺しあって」,大きな床反力を得ることができないので,そのためには,下肢などの運動で作られた加速度が,最も質量の大きい体幹回りで「ぐらつかない」ことが重要となるといえる.もしぐらついてしまうと,それは目的の運動にとっての「エネルギーの漏れ」となってしまう.
体幹トレーニング
このようなエネルギーの漏れを起こさず,効率よく力を発揮させることが近年の体幹トレーニングの重要性が叫ばれている理由のひとつと考えられる.特に深部の筋肉は,その周辺部の力(加速度)によって動かされる力に負けないように,すなわちエネルギーが漏れ出さないようにし,力やエネルギーを伝達したり,体幹全体の加速度で大きな動力を生み出す役割を果たしていると考えられる.
消散エネルギー
また,筋肉には高速に収縮するほど,筋肉自身の収縮にエネルギーを消費してしまうので,筋肉の外部に対して大きな力を与える余力が減ってしまう.また,高速な運動自体が力学的エネルギーの損出になる.このことから,筋肉を収縮速度が小さくなるように,すなわち,いわばアイソメトリックな状態に近づけるように力を発揮することで,筋肉の外部に対して最大限の力を発揮し,仕事をすることが可能となる.そこで,特に動力源となる部位では収縮速度が大きくなるように動かすよりも,大きな加速度を発揮するような動かし方(一般に力感があっても,速度は小さい動かし方)が重要と言える.
4.反力と身体運動

大きな力を発揮するためには,何かを押すことで初めて大きな反力を得ることができる.したがって硬いものや重たいものなどを押すことで,大きな反力が生まれるが,押す対象がなければ大きな反力は得られない.
スポーツに限らず多くの身体運動でも,地面を押すことで反力を得て,その力を身体運動に有効利用している.

ランニングのように直接,地面を蹴る力が直接身体重心方向に作用し,これが移動の動力源になるのでわかりやすいが,床反力が唯一の動力源ということを考えれば,ゴルフスイングのような運動でも,床反力が動力源であることには変わりがない.
たとえば,ゴルフスイングなら床反力をクラブに伝達し,野球の投球ならボールに伝達する.このように,身体重心よりもさらに離れた手先にあり,軽いボールやクラブなどの道具に伝達する運動の場合,床反力が伝達していくことがイメージしにくいかもしれないが,実は,スイング運動でも,スイング(振り子)運動を行うための動力源はやはり床反力が中心で,身体を経由して伝わっていく.
動画ではわかりにくいが,左右の合成の床反力(緑色矢印)が最も大きくなるのが,クラブがほぼ真上に向いたタイミングで,トップの切り返しの直後である.このことは「身体における運動パターン形成 #4」で紹介する予定であるが,クラブに最もエネルギーが伝達されるのもそのあたりで,スイング速度もダウンスイングの前半で決まってしまい,それ以後はいくら頑張ってもクラブにエネルギーを加えることは困難となる.そして,クラブの運動が高速となり,もはや床反力をクラブに伝達することができないダウンスイングの後半では,むしろクラブの回転を邪魔しないように,自然にクラブを回転させることが重要となる.
5.COPの力学
「2.身体重心の力学」で身体重心と床反力の関係について,「4.反力と身体運動」で,身体運動における床反力の意味を述べた.
ここでは,身体重心の力学とCOPの関係について述べていく.
で,フォースプレート側からするとCOPは,フォースプレートに作用する力がバランスする重心点であることを述べた.
では,身体側からするとCOPはどのような意味を持つのであろうか?
ここで,身体を倒立振子と呼ばれる「逆さ箒」として扱い,その意味を考えていきたい.
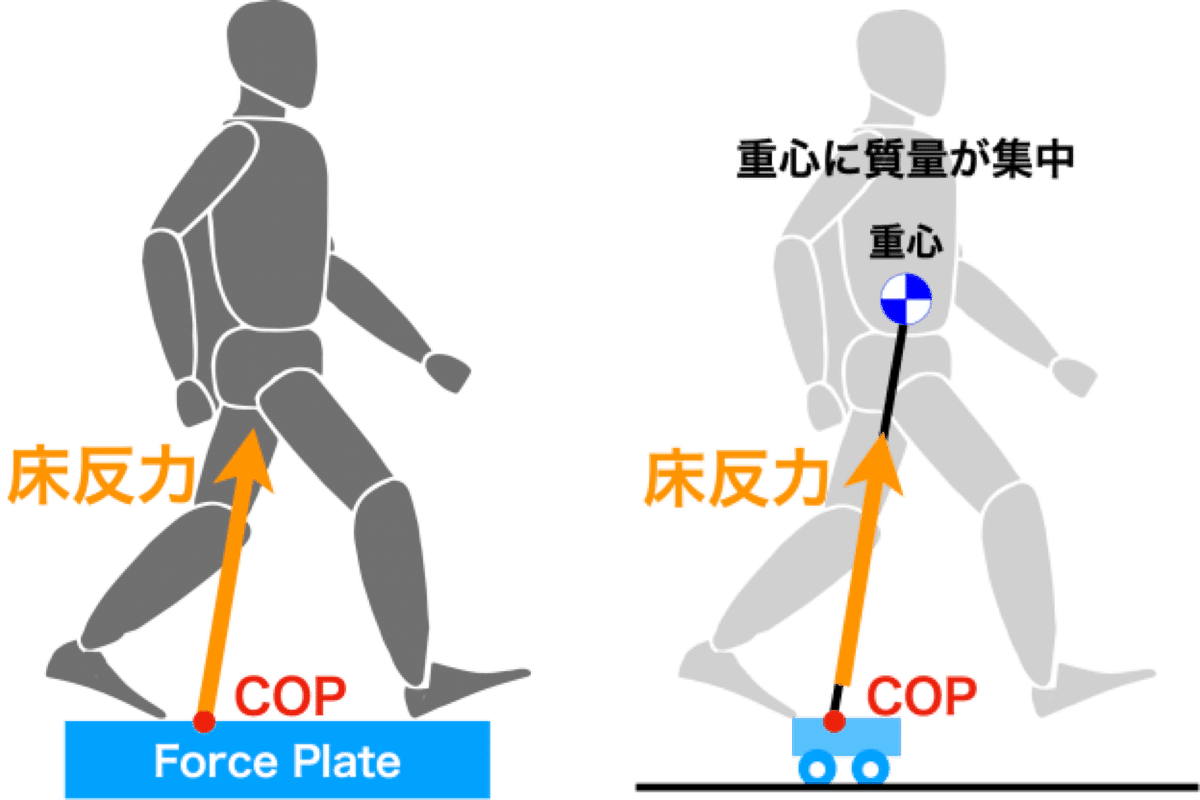
まず,図9左のような歩行やバランス運動を考える.これは人が歩行運動や,立位姿勢のバランス運動でフォースプレートに立つ際にCOPの位置に床反力が作用していると考えてよい.このときの身体は図9右のように,重心に質量が集中したモデルに置き換えることができる.このような置き換えを経て,さらに

図10のような倒立振子に置き換え,歩行やバランス立位のような運動では,身体重心に対して相対的に赤色のCOPの位置を変える制御を行っているとみなすことができる.
つまり,「床反力の大きさ」と,「COP-重心を結ぶ直線」の角度が,運動を決めている.このことから身体運動では,実際の床反力はCOPからほぼ身体重心方向を向くことからも,COPと重心をセットにすることで,身体の制御戦略について多くの情報を得ることができる.
ヒトは重心を移動させることでバランスをとっているように思うかもしれないが.しかし,動かせる範囲も支えている面内に限られるが,COPも積極的に移動させることで姿勢のバランスを取っている.したがってCOPと身体重心の両方の関係をとらえることが重要である.
6.COPとZMP
身体運動においてCOPの意味を述べたが,次にこのCOPが身体のダイナミクスでどのように決まるか考えていく.
COPの定義では,床反力に作用する力のモーメントの水平成分がバランスする点が,COPであった.同じことは身体側からもいえる.

そこで,先程の倒立振子モデルを導入すると,身体側から見たCOPの位置は,同様に床反力が作る力のモーメント$${\bm{M}_c}$$の水平成分がバランスする点(0となる点)として導入することができる.そこで,床面を原点とする座標系$${\text{C}}$$を考え,COPの位置ベクトルを$${\bm{p}_c=[p_x~p_y~0]}$$,身体重心の位置ベクトルを$${\bm{X}_g=[X_g~Y_g~Z_g]^T}$$,重力加速度ベクトルを$${\bm{g}=[0~0~-g]^T}$$とすれば,座標系$${\text{C}}$$からみた,床反力$${\bm{F}}$$が作る力のモーメント$${\bm{M}_c}$$は,
$$
\bm{M}_c = \bm{p}_c \times \bm{F} \\ = \bm{p}_c \times M(\ddot{\bm{X}}_G - \bm{g})
$$
と書け,この水平成分を0として解くことによって,身体側から見たCOPの座標$${(p_x, p_y)}$$
$$
\bm{p}_c = \begin{bmatrix}p_x\\p_y\\0\end{bmatrix} = \begin{bmatrix}X_g - \frac{\ddot{X}_g}{\ddot{Z}_g+g} Z_g \\ Y_g - \frac{\ddot{Y}_g}{\ddot{Z}_g+g} Z_g \\0 \end{bmatrix}
$$
が与えられる.
これは,フォースプレート側の力学で導出した「床に作用する力のモーメントの水平成分が0となり,バランスする重心点」として,
で導出したように,同じCOPの位置を身体側の力学によって導出しただけである.この導出については,このCOPの導出とほぼ同じで簡単であるので,練習問題として残しておく.
注意点
ただし,この際,身体を質点モデルで表すという仮定を用いているので,これは近似が含まれている.歩行やバランス運動などではこの近似は十分成り立っている.
ZMPとCOP
この身体側の力学から導出したCOPは,もはや地面側から見た圧力の中心ではなく,力のモーメントが零になるという意味からロボティクスではZMP(Zero Moment Point)と呼ばれる.COPとZMPは等価であるが,本シリーズでも,フォースプレートから計測した圧力中心としてCOPという用語を用い,ZMPは身体の重心側から計算した水平の力のモーメントがバランスする点として用いる
ヒューマノイドロボットの制御では,目標値としてZMPを定め,ロボットの歩行制御のためにZMPを利用している.
7.ZMPの幾何学的意味
前節で,COPとZMPの物理的意味が,床反力が作る力のモーメントの水平成分がバランスする点であることを述べたが,ここではさらにZMPが幾何学的にどのように定まるかを述べていく.
そこで,ここでもう一度,ZMPの式を以下に示すと,
$$
p_x = X_g - \frac{\ddot{X}_g}{\ddot{Z}_g+g} Z_g \\ p_y = Y_g - \frac{\ddot{Y}_g}{\ddot{Z}_g+g} Z_g
$$
であった.ここで前後方向を$${x}$$軸と定め,$${zx}$$平面を考えると,図12のようになる.

するとこの式は,$${zx}$$平面内で床反力は$${x}$$成分が$${M\ddot{X}_G}$$,鉛直成分が$${M(\ddot{Z}_G+g)}$$となるので,身体重心$${(X_G, Z_G)}$$からみて,角度$${\tan^{-1}\left(\frac{\ddot{X}_G}{\ddot{Z}_G+g}\right)}$$の方向にZMPが位置していることを示している.そして,$${yz}$$平面でも,全く同様である.
以上から,ZMP(COP)の位置$${\bm{p}_c}$$を起点として身体重心$${\bm{X}_G}$$への方向を,または逆に$${\bm{X}_G}$$から$${\bm{p}_c}$$の方向を得ることができるが,ここで重要なことは,その方向は床反力ベクトル$${\bm{F}}$$,または身体重心の加速度と重力加速度$${\ddot{\bm{X}}_G -\bm{g}}$$が定めているということである.
ただし,ランニングなどのように動的で角運動量変化が大きい場合は,近似が成り立たない可能性があるので注意されたい.その場合は,全身の角運動量変化(全身の回転の力学)もモーメントのバランスに考慮する必要がある.ZMPの導出は,参考文献を参考にされたい.
逆さ箒(倒立振子)のバランス運動では,COPが柄の先に,身体重心が箒の重心に相当するが,身体運動でも柄の先の位置と箒の角度でバランスの調整をしていることに相当する.
8.重心動揺計
COPと鉛直方向の床反力に限定して算出する目的のフォースプレートは,一般に重心動揺計と呼ばれている.COPの計算では床反力の鉛直方向成分だけが必要であるため,3方向の力計測が不要で,鉛直方向の力だけ計測する3つの荷重センサと,比較的小型のプレートで構成される.
しかし,前述のとおり,COPは重心位置を示しているわけではない.バランス運動をしている時,たしかに重心の動きを補償するように,COPの位置が動かすことになるので,COPの位置は重心とは反対方向に移動することで,その変動の大きさは,重心の変動の大きさをおおよそ反映しているが,厳密には重心の変動とは全く別物であることに注意をされたい.
参考文献
1)ヒューマノイドロボット(改訂2版),梶田秀司編著,オーム社


【解析・受託開発について】
スポーツセンシングでは,豊富な知見を持つ,研究者や各種エンジニアが研究・開発のお手伝いをしております.研究・開発でお困りの方は,ぜひスポーツセンシングにご相談ください.
【例】
・データ解析の代行
・受託開発
(ハードウェア、組込みソフトウェア、PC/モバイルアプリ)
・測定システム構築に関するコンサルティング など
その他,幅広い分野をカバーしておりますので,まずはお気軽にお問い合わせください.
株式会社スポーツセンシング
【ホームページ】sports-sensing.com
【Facebook】sports.sensing
【Twitter】Sports_Sensing
【メール】support@sports-sensing.com
