
はじめての線形代数part4 ~Aⁿを求めよう!(行列式、余因子の展開編)
はじめに
逆行列の作り方は2つあります。
簡約化をする方法
$${\dfrac{余因子行列}{行列式}}$$の計算をする方法
の2つです。
行列式
余因子行列÷行列式=逆行列
2つ目の余因子行列÷行列式の計算をする方法を見ていきましょう。この内容を理解するには行列式と余因子行列を相互に理解する必要があります。例えば、行列式の勉強に余因子の知識が登場するなどです。
行列式の意義(逆行列の材料)
先に行列式を解説します。結論からいうと、行列式は数字です。ベクトルでもなければ方程式でもありません。表記は絶対値記号をつける($${|A|}$$)、もしくは$${detA}$$と表記します。絶対値記号を付けてはいますが、行列式の値は負もあり得ます。$${detA=|A|=-1}$$なども普通にあります。
既に行列式を勉強している方は、行列式にはどのような意味があるのかと思う方もいると思います。1次変換の拡大倍率と調べたら出てくるかもしれませんが、イメージが掴みずらいと思います。
そこで、行列式とは逆行列を作る材料と捉えてください。存在意義を求めてはいけません。計算さえできればよいのです。
計算方法を解説します。実は何行何列かで計算方法が変わります。これから見やすさのために、n行n列の行列をn×n行列と表記します。
行列式の求め方には「3×3以下の行列」、「4×4以上の行列」の4パターンに分かれます。「サラスの方法」を使うか、「展開」をしていくかの2パターンです。
3×3以下の行列式
1×1の場合
1×1の場合は簡単です。1×1の行列の成分がそのまま行列式の値になります。具体的には
$${A=\begin{pmatrix}2\end{pmatrix}ならば|A|=2\\B=\begin{pmatrix}-10\end{pmatrix}ならば|B|=-10\\C=\begin{pmatrix}\pi\end{pmatrix}ならば|C|=\pi}$$などです。$${B}$$のように行列式を表現するには、$${||}$$で表現しますが、絶対値のように正にする必要はないです。
2×2と3×3の場合(サラスの方法)
ここからは、筆者の数学の表現に限界があるため、画像を挿入する形で解説します。2×2行列と3×3行列を以下のように表現します。

2×2行列と3×3行列の計算は「サラスの方法」を利用します。「サラスの方法」とは以下の画像の順のように行列の成分の積を取ります。次に足し引きする方法です。なお、サラスの方法は2×2,3×3行列の時のみしか使えません。4×4以上の行列は使えません。
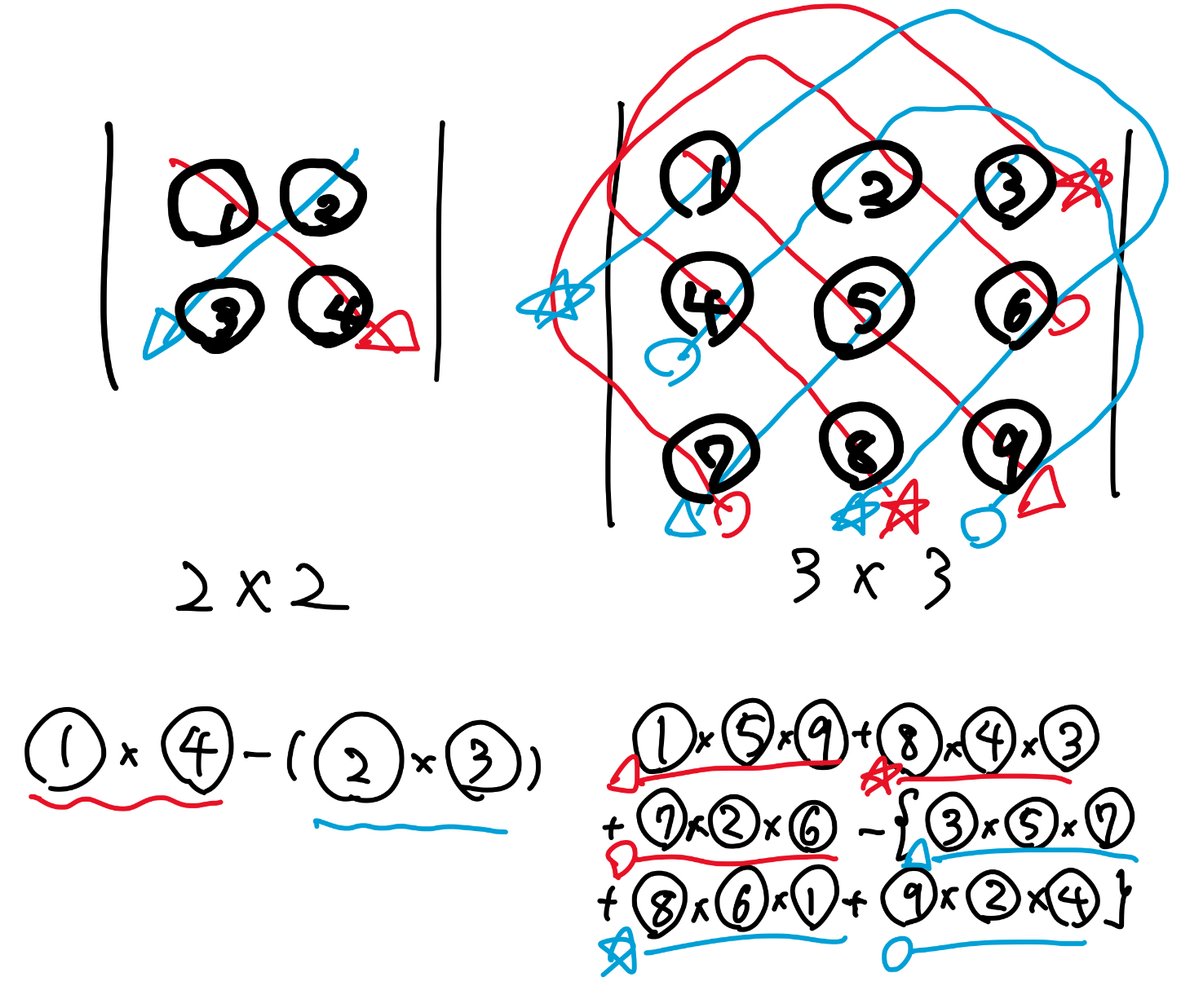
なぜ以下の順になるのかを理解するのはかなり難しいので後日別枠で解説をしようと思います。
実際に計算してみよう!(サラスの方法)
ここで例題を解いてみましょう。行列式は数なので「$${=}$$」の記号が使えます。$${\begin{vmatrix} 1&-2\\ 3&1\end{vmatrix}=(1)(1)-(-2)(3)=1+6=7}$$ $${\begin{vmatrix}-2&-1&0\\ 1&1&-2\\-1&3&1\end{vmatrix}=\lbrace(-2)(1)(1)+(3)(1)(0)+(-1)(-1)(-2)\rbrace-\lbrace(0)(1)(-1)+(3)(-2)(-2)+(1)(-1)(1)\rbrace=(-2+0-2)-\lbrace(0+12-1) \rbrace=-15}$$

4×4以上の行列式
次に4×4以上の行列を見ていきましょう。結論からいうと、①余因子行列を求める操作を使うことで3×3行列に変形させてから、②サラスの方法で求める、①②の順で求めます。先ほども記述しましたが、4×4以上の行列のときにはサラスの方法は使えないので、地道に計算していく必要があります。
「余因子行列を求める操作」について、いくつか単語を確認しましょう。
小行列・・・行列です。「とある成分」のある行とある列を除いてできる、一回り小さくなった行列です。
小行列式・・数です。小行列の行列式です。
展開する・・行列式(数)を作ります。行列式の大きさを1つ小さくします。以下の操作です。$${\\「(とある成分)×(-1^{(とある成分の行数+列数)})×(小行列式)」\\を(とある行or列)について足していく操作。}$$


単語を可視化すると上図となります。初めは展開の操作に戸惑うかもしれません。図で見ると、展開をすることは、「行列式の大きさを一回り小さくする」ことを意味します。上記だと、3×3を2×2にしています。(なぜ、展開前の行列式と展開後の行列式の和は同値になるのかの説明も後日解説を作ろうと思います。)
つまり、4×4以上の行列は展開を繰り返すことで3×3行列に変形させることで行列式が求まります。
実際に計算してみよう!(4×4以上の行列)
4×4以上の行列式を展開を用いて解いていきましょう。3×3行列のときのサラスの方法を使う途中式は省略します。
$${\begin{vmatrix}1&0&2&2\\3&1&-2&0\\-2&1&1&3\\-1&0&2&1\end{vmatrix}=1×(-1)^{(1+1)}\begin{vmatrix}1&-2&0\\1&1&3\\0&2&1\end{vmatrix}+0×(-1)^{(1+3)}\begin{vmatrix}3&-2&0\\-2&1&3\\-1&2&1\end{vmatrix}\\+2×(-1)^{(1+3)}\begin{vmatrix}3&1&0\\-2&1&3\\-1&0&1\end{vmatrix}+2×(-1)^{(1+4)}\begin{vmatrix}3&1&-2\\-2&1&1\\-1&0&2\end{vmatrix}\\=1×(1-4)+2×(0+2)-2×(5+2)=-13}$$

ちょっとしたテクニック
今からの話は行列式にしか使えないテクニックです。後の余因子行列とは無関係な話です。
行列式ではある行(または列)を何倍かして別の行(または列)に足しても値が同じになるのです。ある行の何倍かを別の列には足せません、あくまで行の時は行に、列の時は列に、です。
今解いた4×4行列なら、1行目$${\begin{pmatrix}1&0&2&2\end{pmatrix}}$$の-3倍を2行目に足す、2倍を3行目に、1倍(そのまま)を4行目に足すなどができるのです。今の操作は
$${\begin{pmatrix}1&0&2&2\\3-3×1&1-3×0&-2-3×2&0-3×2\\-2+2×1&1+2×0&1+2×2&3+2×2\\-1+1&0+0&2+2&1+2\end{pmatrix}=\begin{pmatrix}1&0&2&2\\0&1&-8&-6\\0&1&5&7\\0&0&4&3\end{pmatrix}=1(-1)^{(1+1)}\begin{vmatrix}1&-8&-6\\1&5&7\\0&4&3\end{vmatrix}+0+0=-13}$$と展開するときに非常に楽になるのです!
余因子行列
行列式を攻略しました。後は余因子行列とは何者かを攻略すれば、逆行列が求まります。ここでも単語を確認しましょう。
余因子・・・・数字のことです。余因子行列の成分になります。$${\\「(-1^{(とある成分の行数+列数)})×(小行列式)」}$$
転置する・・・行と列を入れ替える操作。イメージは斜めに軸を取って回転させることです。$${t}$$が左上に乗り、$${^t\!A}$$ と書かれます。
余因子行列・・行列です。とある成分の位置に余因子を並べてできる行列を転置させてできる行列

転置・・・行と列を入れ替える操作。イメージは斜めに軸を取って回転

実際に計算してみよう!(余因子行列)
とても頭がこんがらがる作業です。しかし一度慣れてしまえばとても便利な作業なので例題で詳しく見ていきましょう。
$${A=\begin{pmatrix}1&4\\-3&7\end{pmatrix}\\B=\begin{pmatrix}1&2&-1\\-2&0&-1\\-1&-1&0\end{pmatrix}\\のときA,Bの余因子行列を求めよ。\\Aの場合:各行と列における余因子を並べると\\\begin{pmatrix}①:7&②:3\\③:-4&④:1\end{pmatrix}\\これを転置して\begin{pmatrix}7&-4\\3&1\end{pmatrix}\\(①:7=(-1)^{(1+1)}×|7|,②:3=(-1)^{(1+2)}×|-3|,\\③:(-1)^{(2+1)}×|4|,④:(-1)^{(2+2)}×|1|)\\Bの場合:余因子を並べると\\\begin{pmatrix}①:1&②:-1&③:2\\④:1&⑤:-2&⑥:4\\⑦:-1&⑧:1&⑨:-3\end{pmatrix}\\これを転置して\\\begin{pmatrix}1&1&-1\\-1&-2&1\\2&4&-3\end{pmatrix}\\①:1=(-1)^{(1+1)}\begin{vmatrix}1&0\\2&1\end{vmatrix},②:-1=(-1)^{(1+2)}\begin{vmatrix}1&0\\0&1\end{vmatrix}\\③:2=(-1)^{(1+3)}\begin{vmatrix}1&1\\0&2\end{vmatrix},④:1=(-1)^{(2+1)}\begin{vmatrix}1&1\\2&1\end{vmatrix}\\⑤:-2=(-1)^{(2+2)}\begin{vmatrix}-2&1\\0&1\end{vmatrix},⑥:4=(-1)^{(2+3)}\begin{vmatrix}-2&1\\0&2\end{vmatrix}\\⑦:-1=(-1)^{(3+1)}\begin{vmatrix}1&1\\2&1\end{vmatrix},⑧:1=(-1)^{(3+2)}\begin{vmatrix}-2&1\\1&0\end{vmatrix}\\⑨:-3=(-1)^{(3+3)}\begin{vmatrix}-2&1\\1&1\end{vmatrix}}$$
逆行列を求めよう
さて、逆行列は$${\dfrac{余因子行列}{逆行列}}$$でした。前回同様に$${A=\begin{pmatrix}3&5\\1&2\end{pmatrix}}$$として、$${A^{-1}}$$を求めてみましょう。
まずは行列式$${|A|}$$を求めます。
$${|A|=3×2-5×1=1}$$
次に余因子行列を求めます。各行と列における余因子を並べると
$${\begin{pmatrix}①:2&②:-1\\③:-5&④:3\end{pmatrix}}$$となり、これを転置すると。
$${\begin{pmatrix}2&-5\\-1&3\end{pmatrix}}$$
$${①:(-1)^{(1+1)}×|2|\\②:(-1)^{(1+2)}×|1|\\③:(-1)^{(2+1)×|5|}\\④:(-1)^{(2+2)}×|3|}$$
前回同様の結果になりました。これで逆行列を求める方法を2通り学習しました。
2つの使い分け
逆行列の求め方として簡約化だけ習得すればよいのでは、わざわざ行列式や展開などを勉強する必要はないのでは、と考える方もいると思います。
たしかに、2×2行列の場合は簡約化のほうがスムーズかもしれません。しかし、3×3、4×4などになると簡約化では計算ミスを誘発しかねません。
簡約化は手順が楽な代わりに、計算ミスが起こりやすいです。$${\frac{余因子行列}{行列式}}$$は計算ミスを防げたり、工夫次第で楽に計算ができる代わりに、手順がかなり厄介です。
両者はトレードオフの関係なので、どちらも学んでおいて損はないです。
おわりに
目標である$${A^n}$$を求めるには
$${A}$$をどうにかして、対角行列$${P^{-1}AP}$$にする。
$${P^{-1}AP}$$をn乗する
$${(P^{-1}AP)^n}$$をどうにかして$${A^n}$$に戻す。
をするのでした。
逆行列を求めれるようになったので$${P^{-1}}$$を求めることができるようになりました。
次回は対角行列にする技術を扱います。最後まで見ていただきありがとうございました!
問題
追記:問題を作りました!答えはこちらから!
はじめての線形代数 練習問題4
基本問題
$${問1.行列 A と B について、 A ,Bの行列式を求めよ。\\A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}, \quad B = \begin{pmatrix} -1 & 0 \\ 5 & 1 \end{pmatrix}\\}$$
$${問2.以下の行列 A の行列式を求めよ。\\A = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \\ 7 & 8 & 9 \end{pmatrix}}$$
$${問3.以下の行列 A の行列式を求めよ。\\A = \begin{pmatrix} 1 & 2 & 3 & 4 \\ 5 & 6 & 7 & 8 \\ 9 & 10 & 11 & 12 \\ 13 & 14 & 15 & 16 \end{pmatrix}}$$
応用問題
$${問4.以下の行列 A の逆行列を、余因子行列と行列式を用いて求めよ。\\A = \begin{pmatrix} 2 & 3 \\ 4 & 1 \end{pmatrix}}$$
$${問5.以下の行列 B の行列式を余因子展開を利用して求めよ。\\B = \begin{pmatrix} 1 & 2 & 3 \\ 4 & 5 & 4 \\ 1 & 1 & 1 \end{pmatrix}}$$
$${問6.行列Cの逆行列を余因子行列を行列式で除して求めよ。\\C = \begin{pmatrix} 1 & 1 & 0 & 0 \\ -2 & 1 & 2 & 0 \\ 0 & 1 & 1 & 2 \\ 0 & 0 & 1 & 2 \end{pmatrix} }$$
