中学生への数学教育について思うこと(前編)
全般的に思うこと
子供たちに何を教えるべきかということについて、私たちは時代の変化を読むことができないので、あまり変わらない基礎的な事項を教えていく方がよいと思います。
高校数学とのつながりが大切なことであり、すぐにキャッチアップできる内容は優先度が低いと思います。
その考えでいくと「D データの活用」はすぐにその人が必要になった時に学べばよいような内容なので、正直学習項目から外してでも他に注力すべきだと私は思います。
その時代のメインツールとなっているアプリケーションやプログラミングを使ってデータ処理として学んだらよい内容だろうと思います。
今後の AIの発展を考えると、これからの子供たちに必要なことはスキルではないと思います。
行動すること、意欲を持つこと、没頭すること、そしてその結果として何かを創造し発想することだと思います。
非常に高いスキルをもった AI という存在が従業員として存在している社長のようなものですから、部下である AI に対してこういったことをやりたいという「インプット」や結論に対して「理解」をする必要があります。
この理解のために教育があるとイメージしたとき、例えば解の公式を覚えている必要はないでしょうが、それが二次方程式の答えが導けることを理解している必要はあり、テスト用紙に書いてあれば、それを使って答えを出せる必要は依然として存在するということになります。
つまり教育は要らなくなるということではなく、解き方を頑張って暗記するといったこれまでのスキルのようなものではなく、もう少し基本的である意味より本質的な理解が必要になるだろうと思います。
教育する項目は保守的でいいと思いますが、数学に関わらず学校システムは変化したほうがいいと思います。
いくつか自分の考えている具体例を列挙しました。
〇 部活は地域のクラブに変更したほうがよい
これは少子化の今、部活はその学校だけで成り立たなくなると思いますので、範囲を広げる必要があるだろうと考えての意見になります。
〇 出題される問題は基本的内容に絞り、解法暗記の時間を減らす。
現状では時間内に解くために解法暗記は重要ではありますが、過去に投稿したように、基本的事項を理解していれば大学に合格するとすれば点数差別化のための難問・奇問は不要になると思います。
〇 授業を単位制にする
内容を簡単にするかわりに早めに中学の内容を終えることも可能にした方がいいと思います。
数学は始めが一番難しい概念が難しい学問です。
その難しい概念を1年次に固めていることも数学が苦手になっていく要因だと思います。
そのため時間の確保やカスタマイズができるように単位制にすることを提案します。
また稀にすごい賢い子供も存在しますので、そういった子供はどんどん先に進んでいってもらえればよいと思います。
本当の問題は答えがあるか分からないところにあります。
その問題を解くのに中学生までで学んだことで解きなさいという縛りは存在しません。
〇 動画や個人学習を促すためのツールとの連携、及び先生の役割
単位制にする場合基本動画等で学んでいき、先生はチューターのような存在になればよいと思います。
時代の変化はこれからますます加速するので、必要なことを自分で学んでいくことが大切です。
この個人学習の始まりを中学生から始めればよいと思います。
ただ小学生にはこういった姿勢は要求しません。
人から教わるという色々な刺激が必要な段階というものは確かに存在するだろうと、コロナの状況下における教育を見て感じました。
以下に、「中学校学習指導要領(平成 29 年告示)解説 数学編」を元に自分の意見や私の考えるキーポイントを書いていきたいと思います。
A 数と式
中学数学において最も重要なことは「文字」を使うという点である。
私はこのメリットや意図を理解してもらうためには全体像を先にみせておいたほうがいいと思います。
方程式や関数っていう便利な考え方があり、現時点で計算して解ける必要はないがこういうことができるということを先にみせておいたほうがいいと思います。
少なくとも私は意味の分からない文字の計算をひたすらやらされるのは苦痛でしかありませんでした。
第1学年
A(1) 正の数と負の数
(1) 正の数と負の数について,数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
ア 正の数と負の数の必要性と意味を理解すること。
イ 正の数と負の数の四則計算をすること。
ウ 具体的な場面で正の数と負の数を用いて表したり処理したりするこ
と。
イ 次のような思考力,判断力,表現力等を身に付けること。
ア 算数で学習した数の四則計算と関連付けて,正の数と負の数の四則計
算の方法を考察し表現すること。
イ 正の数と負の数を具体的な場面で活用すること。
〔用語・記号〕
自然数 素数 符号 絶対値
[内容の取扱い]
(1) 内容の「A数と式」の(1)に関連して,自然数を素数の積として表すことを取り扱うものとする。
(2) 内容の「A数と式」の(1)のアとイのアに関連して,数の集合と四則計算の可能性を取り扱うものとする。
[意見]
割り算は分数を生み出し、引き算は負の数を生み出しました。
また新しい数が加わりましたが、計算方法については理屈をしっかり教えつつ、ある程度慣れの部分もあると思います。
また引き算と負の数は混乱しやすいので、引き算は操作であり、負の数は数であるということを強調したほうがいいと思います。
素因数分解も出てくるわけですが、大事なことは分解した素数の積は一意的に定まるという点です。
これは文字を使って説明したほうがいいと思いますが、先に一意的に定まると言い切ってしまってもいいかもしれません。
[私の考えるキーポイント]
1)数直線でみる負の数
ある基準を決めた時、小学生まではプラスの方向の数のみ考えてきました。ですが例えば水が凍る温度を 0 としたとき、それより低い温度が存在します。
また今の時間を 0 としたとき、それより1時間前という時間も存在します。そこでプラスの方向の逆の数である負の数という考えを導入してみましょう。
負の数は正の数を 0 を中心に折り返した数です。数を直線状で表した数直線で考えると以下の図のようになります。

数直線上の右側に行くほど大きい数です。
つまり (-4) より (-3) の方が大きい数ということになります。
正の数の 4 は 3 より大きい数なので、負の数になると逆転するということになります。
絶対値という考えも紹介しておきます。
絶対値とは 0 からの距離のことです。
(-4) の絶対値は、4 となりますので、単に正と負の符号を無視した数と理解しておいてください。
正の数と負の数を計算したときに、答えが正の数になるか、負の数になるかを考える上で非常に役立つ考え方になります。
2)負の数を含めた足し算と引き算(矢印で考える)
<(正の数)+ (正の数)>
これは算数で習った通りです。矢印の方向に数を進めます。
計算例)2+3=5

<(正の数)ー(正の数)>
小学校の時は計算できなかった、引く数の方が大きい場合について示します。
引くときは、矢印を逆向きにした方向に進めることになります。
計算例)2-3=(-1)

<(正の数)+(負の数)>
数を足すときは矢印の方向は変えません。
そのため以下の関係が成立します。
(正の数)+(負の数) = (正の数) ー (正の数)
計算例)2+(-3)=2-3=(-1)
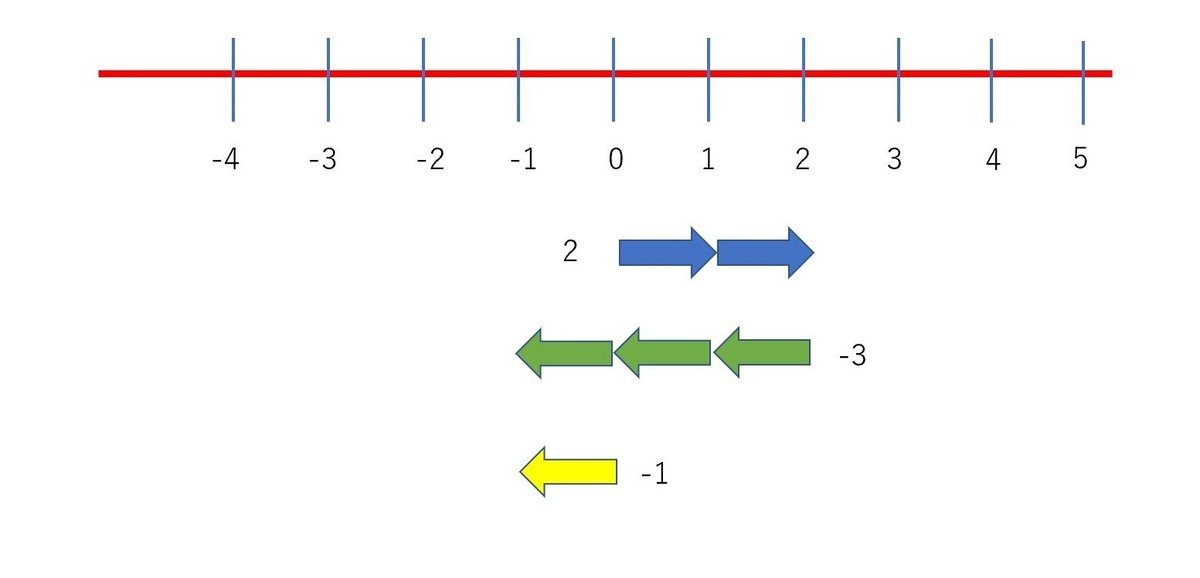
<(正の数) ー(負の数)>
数を引くときは矢印を逆向きにします。
そのため負の数を引くということは正の数を足すことになります。
計算例)2-(-3)=2+3=5

毎回数直線を考えるのは、大変なので計算方法についてまとめてみます。
計算して出てくる答えは(-3)のように符号と絶対値を合わせたものになりますので、それぞれ分けて考えることができます。
手順1) 引き算の場合、足し算に書き換える。
-(正の数)=+(負の数)
-(負の数)=+(正の数)
手順2) 同じ符号の場合、符号はそのままで絶対値を足す
(+3)+(+4)=+7
(-3)+(-4)=-7
手順3) 異なる符号の場合、絶対値が大きいほうの符号を使用して、絶対値の大きい数から小さい数を引く。
(-4)+(+3)=-(4-3)=-1
(-3)+(+4)=+(4-3)=+1
3)負の数を含めたかけ算と割り算(進む向きと時間で考える)
負の数のかけ算について理解するためには、二つの要素が必要になります。そこで速さと時間で考えてみましょう。
右向きに進むことを正の数と考えると、西向きに進むことは負の数になります。
現時点から 1時間後を正の数と考えると、1時間前は負の数になります。
現時点では 0 の位置にいるとして、具体的に計算していこうと思います。
<(正の数)×(正の数)>
右向きに1時間当たり、2 進むとします。
3時間後どこにいるか計算します。
計算式:(速度)×(時間)=(+2)×(+3)=(+6)

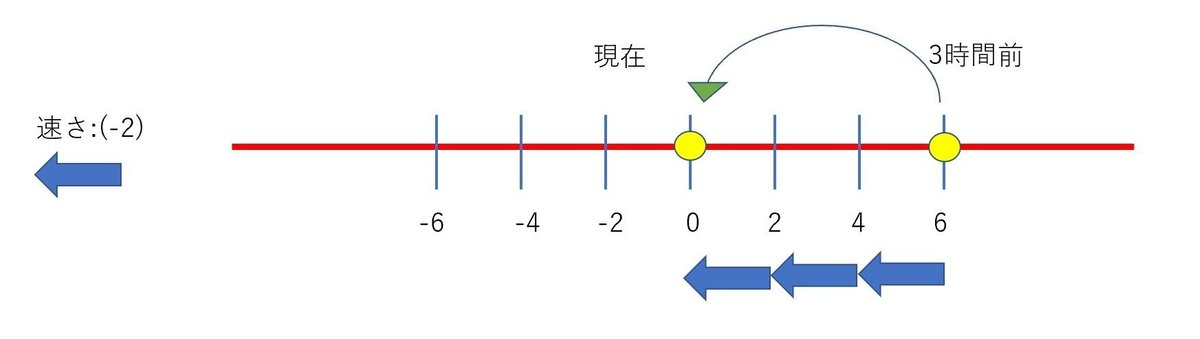
<(正の数)×(負の数)>
右向きに1時間当たり、2 進むとします。
3時間前にどこにいるか計算します。
計算式:(速度)×(時間)=(+2)×(-3)=(-6)
確かに(-6)の位置にいれば、3時間後 0 の位置にいることが分かります。

<負の数)×(正の数)>
左向きに1時間当たり、2 進むとします。
3時間後にどこにいるか計算します。
計算式:(速度)×(時間)=(-2)×(+3)=(-6)
3時間後 (-6) の位置にいることが分かります。

<(負の数)×(負の数)>
左向きに1時間当たり、2 進むとします。
3時間前にどこにいるか計算します。
計算式:(速度)×(時間)=(-2)×(-3)=(+6)
確かに(+6)の位置にいれば、3時間後 0 の位置にいることが分かります。
<負の数のかけ算のまとめ>
負の数のかけ算は符号には規則性があり、絶対値はかけ算になることが分かりました。
負の数が1回掛かると負の数になり、2回掛かると正の数になります。
(-)×(+)=(-)
(-)×(-)=(+)
負の数が3回掛かると負の数になり、4回掛かると正の数になります。
つまり負の数が奇数回かかると負の数、偶数回かかると正の数になります。
(-)×(-)×(-)=(+)×(-)=(-)
(-)×(-)×(-)×(-)=(+)×(+)=(+)
<負の数の割り算>
割り算は分母と分子が逆にしてかけ算をするだけなので、符号の規則性はかけ算と同じで、絶対値は逆数のかけ算となります。
$${6÷(-3)=-(6÷3)=-(6×\frac{1}{3})=-2}$$
<累乗>
同じ数を何回もかけることを累乗といいます。
負の数が偶数回あらわるか、奇数回あらわるか気をつける必要があります。
$${(+3)^3=(+3)×(+3)×(+3)=(+27)}$$
$${(-3)^2=(-3)×(-3)=(+9)}$$
$${(-3)^3=(-3)×(-3)×(-3)=(-27)}$$
以下の様な紛らわしい表記もあるので、何を一つの固まりとしてみているか理解してもらう必要があります。
$${(-3)^2=(-3)×(-3)=(+9)}$$
$${-3^2=-(3×3)=(-9)}$$
4)整数は素数の積となり、その組み合わせは一通りに決まる
1とその数自身しか約数がない数を素数といいます。
(1は素数ではありません。)
自然数を素数だけの積であらわすことを素因数分解といいます。
例えば 90 を素因数分解すると
90=2×45=2×3×15=2×3×3×5
$${90=2×3^2×5}$$
つまり90は2が1つ、3が2つ、5が1つのかけ算の積になるということで、一つに定まります。
ちなみにここで1を素数とすると、1は何回かけてもよいので、1が3つのケースや4つのケースが発生し一通りで定まらなくなるので、1は素数ではなくなるわけです。
また一通りに定まることを説明することもできますが、文字を使う説明になるので後回しでもよいかと思います。
数学的にもう少し厳密にするためには高校生になってからの説明になると思いますが、中学生用に説明すると以下のような内容になると思います。
<説明>
ある整数がabcと素因数分解できたとします。
もう一通りdefと素因数分解できたとします。
abc=def となるわけですが、両辺をaで割ると、右辺も当然aを約数としてもっていないといけないわけです。
bで割る、cで割ると繰り返したとき、左辺は1となりますので、右辺も1になる必要があるので、一旦defと置きましたが、それはabcの積になる必要があるということです。
これは3つ以上の文字であろうと同じです。
A(2) 文字を用いた式
(2) 文字を用いた式について,数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
ア 文字を用いることの必要性と意味を理解すること。
イ 文字を用いた式における乗法と除法の表し方を知ること。
ウ 簡単な一次式の加法と減法の計算をすること。
エ 数量の関係や法則などを文字を用いた式に表すことができることを理解し,式を用いて表したり読み取ったりすること。
イ 次のような思考力,判断力,表現力等を身に付けること。
ア 具体的な場面と関連付けて,一次式の加法と減法の計算の方法を考察し表現すること。
〔用語・記号〕
項 係数 ≦ ≧
[内容の取扱い]
(3) 内容の「A数と式」の(2)のアのエに関連して,大小関係を不等式を用いて表すことを取り扱うものとする。
[意見]
多くの人が数学を嫌いになる分野だと思います。
私もここで数学を嫌いになりかけました。
私が嫌いになりかけた理由は、なぜこんな計算をしているのかよく分からないという点でした。
そこでまず「なぜ文字式を学ぶか」という話が必要だと思います。
文字を使う理由は実際の数(固定された数)を使うと表現しづらいですが、すごく役に立つ考え方があるからです。
それはこの後に学ぶことになる「方程式」と「関数」で使うためです。
1)方程式についてざっくりと
方程式はまだわかっていない数や求めたい数を文字にして、とりあえず等式を成立させ、あとからその数を求める方法です。
式を立てれば、あとは式が勝手に答えを考えてくれるといった感覚です。
例えばリンゴを100円で売るとします。
売上が1500円になるためには何個売ればよいかという課題にあなたが直面したとします。
何個売ればよいかという数を a 個とします。
(リンゴ1個の値段)×(売り上げの個数)=(売上)
という関係性がありますので、
100 × a = 1500
等式が成立しているということは両辺はまるで天秤のようになっているわけです。
そのため同じ数で割ってもよいので、両辺を100で割ります。
a=15
売り上げるべき個数が15個であることが分かります。
この例は簡単ですぐに割り算をすればよいと気づけるでしょうが、より複雑になったときに力を発揮する考え方です。
2)関数についてざっくりと
関数はある変化する数(変数)によって決まる値がある式(関係性)のことです。
方程式では文字はまだ分かっていないけど何らかの値が当てはまるものだったのですが、関数では文字を変化していく数と捉えています。
例えばリンゴを100円で売るとします。
売り上げの個数を変化させたとき、売りあげがいくらになるかということを式であらわすと関数となります。
売り上げの個数を a として、売り上げを y であらわすと以下の式が成立します。
y=100 × a
a が変化するとyが変化していきます。
これを座標というものに点をとっていき、結ぶと変化の様子を表す直線や曲線(グラフ)になります。
これにより変化の様子を見通すことができます。
例えば上の例で、y(売り上げ)=1500 とすると方程式で解いた時と同様、売り上げの個数を求めることができます。
つまり関数のある点に注目すると、そこは方程式となります。
数学という分野は型を作ってくれる分野です。
それを自分の仕事や課題に活かして初めてその真価を発揮すると思います。
例えば私が化学メーカー時代に業務でよく使った考え方は、以下の流れです。
(データを取る:
例. ある圧力をかけて削れる量のデータを取ります)⇒
(点を取ってグラフにし、関数を探す:
例. 圧力と削れる量の関係が満たす関数を探します。)
⇒(求めたい点に注目して方程式としてほしい値を計算する:
例. 特定の量を削るための圧力を算出する)
方程式と関数は非常に役立つ考え方です。
これは具体的な数を使うと上手く表現できません。
そのため未知数や変数を扱うため文字が利用されるわけです。
ここまで話したうえでこの文字式を計算する練習のためにこのセクションがあることを理解してもらった方がよいと思います。
[私の考えるキーポイント]
1)文字式のルール
〇 同じ文字には同じ数が入る(一番大事なルール)
〇 「×」は省く、「÷」は分数で表示
$${a×b=ab}$$
$${a÷b=\frac{a}{b}}$$
〇 数とのかけ算は数を先に書く、「1」は省く
$${3×a=3a}$$
$${1×a×b=ab}$$
$${(-1)×a×b=-ab}$$
〇 同じ文字のかけ算は累乗で表す
$${a×a×b×b×b=a^2b^3}$$
2)文字式の計算
第1学年では「一種類の文字についての一次式の加法と減法が学習の中心」らしいです。
例. 2(3x+4)−3(x−5)
同類項は2年次のキーワードになっていたので、「同類項をまとめよ」ならゴールも分かるのですが、「計算せよ」で終わらせたとき何をもって答えがでたと子供たちに理解してもらうのだろうと思いました。
「展開せよ」の場合は、ばらした時点で答えになるわけなので。
正直単元の切り方に違和感を感じました。
A(3) 一元一次方程式
(3) 一元一次方程式について,数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
ア 方程式の必要性と意味及び方程式の中の文字や解の意味を理解すること。
イ 簡単な一元一次方程式を解くこと。
イ 次のような思考力,判断力,表現力等を身に付けること。
ア 等式の性質を基にして,一元一次方程式を解く方法を考察し表現すること。
イ 一元一次方程式を具体的な場面で活用すること。
〔用語・記号〕
移項
[内容の取扱い]
(4) 内容の「A数と式」の(3)のアのイとイのイに関連して,簡単な比例式を解くことを取り扱うものとする。
[私の考えるキーポイント]
1)等式について
「=」のことを等号といい、等号で関係を表された式を等式といいます。 「=」の 左側の式を左辺、右側の式を右辺といいます。
(左辺)=(右辺)
文字に代入する値によって、成立したりしなかったりする等式を方程式といいます。
方程式が成り立つ値を「方程式の解」といい、解を求めることを「方程式を解く」といいます。
この辺りの言葉の整理が必要になります。
2)天秤の考え方と移項
等式は両辺が同じ値を取るので、同じ値を足し、引き、かけ、割り算することができます。
〇 A=B であれば、A+C=B+C
〇 A=B であれば、AC=BC
〇 A=Bであれば、$${\frac{A}{C}=\frac{B}{C}}$$
(但しC=0では成立しない。)
これらの性質を利用して方程式が解けます。
(例)2x+3x−20=10を解く。
同類項をまとめると 5x−20=10
両辺に +20 します。(操作1)
5x−20+20=10+20
5x=10+20
両辺を +5 で割ります。
5x÷(+5)=30÷(+5)
x=6
操作1の両辺に +20 を足す処理は、左辺から符号を入れ替えて右辺に移動しているように見えるので移項と呼びます。
方程式の場合、解くこと以上に式を立てることが大切です。
分からない数を文字にして、等式を考える必要があります。
第2学年
A(1) 文字を用いた式
(1) 文字を用いた式について,数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
ア 簡単な整式の加法と減法及び単項式の乗法と除法の計算をすること。
イ 具体的な事象の中の数量の関係を文字を用いた式で表したり,式の意味を読み取ったりすること。
ウ 文字を用いた式で数量及び数量の関係を捉え説明できることを理解すること。
エ 目的に応じて,簡単な式を変形すること。
イ 次のような思考力,判断力,表現力等を身に付けること。
ア 具体的な数の計算や既に学習した計算の方法と関連付けて,整式の加法と減法及び単項式の乗法と除法の計算の方法を考察し表現すること。
イ 文字を用いた式を具体的な場面で活用すること。
〔用語・記号〕
同類項
[意見]
「二つの奇数の和は,偶数である」ことを説明するために文字を使った説明が記載されていましたが、離散変数(飛び飛びの変数)を急に導入しているということ、2×(整数)が偶数であることを使っているので、かなりジャンプアップしていることに気を付けなければならないと思います。
[私の考えるキーポイント]
1)言葉の整理
まずは言葉の整理が大切になります。
〇 単項式:数や文字のかけ算で表される式
(例)単独の数字や文字:3 , a 組み合わせ:3a , -3a
〇 多項式:単項式が足し算、または引き算されている式
(例)2x−3xy+4a
〇 同類項:累乗を含む文字部分が全く同じ単項式
(例)$${a^2b}$$と$${−3a^2b}$$は同類項
(例)$${a^2b}$$と$${−3a^2b^2}$$は同類項ではない
〇 係数:単項式の数字部分
(例)2a は 2、x は 1、-x は (-1)
〇 次数:文字式においてかけあわされている文字の数
(例)$${3a^2b}$$は3次(a×a×b)、$${3a^2}$$は2次(a×a)
多項式の次数:それぞれの単項式の次数で最大の値
(例)$${3x^3y+4xy+2x}$$は$${3x^3y}$$の4次式
2)文字式の計算
文字式の計算の目的は「同類項をまとめる」ことで、以下の関係性が最も大事な考え方です。
ax + bx = (a + b)x
(例) 3x+5x=8x
上記関係性が成立することは同じ文字には同じ数が入るということから説明できます。(分配法則)
x=100 であれば 3×100 + 5×100=(3+5)×100=8×100 となります。
これは100円のものを3個買った代金と 100円のものを5個買った代金を合わせた計算する際に、100円のものを8個買った代金を計算することと同じです。
かけ算や割り算は以下のようになります。
〇 かけ算の具体例
$${2a^2b×3ac=2×3×a×a×a×b×c=6a^3bc}$$
〇 割り算の具体例
$${2a^2b÷3ac=\frac{2a^2b}{3ac}=\frac{2×a×a×b}{3×a×c}=\frac{2ab}{3c}}$$
A(2) 連立二元一次方程式
(2) 連立二元一次方程式について,数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
ア 二元一次方程式とその解の意味を理解すること。
イ 連立二元一次方程式の必要性と意味及びその解の意味を理解すると。
ウ 簡単な連立二元一次方程式を解くこと。
イ 次のような思考力,判断力,表現力等を身に付けること。
ア 一元一次方程式と関連付けて,連立二元一次方程式を解く方法を考察し表現すること。
イ 連立二元一次方程式を具体的な場面で活用すること。
[意見]
算数受験で行われる鶴亀算も連立方程式で考えれば、無理なく解けます。
私たちは本当に有効な考え方を得ることができたと実感できる場面だと思います。
[私の考えるキーポイント]
連立方程式では未知数は2つになります。
片方の文字を消すためにもう一つの式を使うことになりますので、未知数の数だけ方程式が必要になるということを分かってもらう必要があると思います。
〇 具体例
50円の消しゴムと100円のシャーペンを合わせて10個買いました。
払った料金が850円のとき、消しゴムとシャーペンをそれぞれ何個買ったでしょう。
〇 解き方
分からない数である消しゴムの数をx個とする。
シャーペンの数は y個とする。
(消しゴムの個数)+(シャーペンの個数)=10
(消しゴムの料金)+(シャーペンの料金)=(払った料金)
上記関係性は以下のようにあらわされる
x+y=10
50x+100y=850
連立方程式では文字を消すことが方針となる。
x=10−y となるので 50x+100y=850に代入
50(10−y)+100y=850
500−50y+100y=850
500+50y=850
両辺に(-500)を足す。
50y=850−500
50y=350
両辺に$${\frac{1}{50}}$$を掛ける。
y=7
x=10−y=10−7=3
消しゴムの個数は 3 個、シャーペンの個数は 7 個
方程式は等式を立てる段階と解く段階があります。
等式を立てる段階で大事なことは分からない数を文字式にして、等式を書くことです。
どの数を文字にするかということは、計算のしやすさという差はありますが、ゴールには辿り着けるのでとりあえずは気にしなくてもよいと思います。
方程式を解くときは、左辺と右辺が天秤で成立しているイメージをもち、同じ数を四則演算しても大丈夫ということが大切です。
そして頑張って (未知数の文字)= の形に持っていく方法を考えてもらいます。
また未知数が複数の場合はその未知数を代入して消していき、1つ求めてその後他の未知数についても求めていくという方針を理解してもらいたいです。
第3学年
A(1) 正の数の平方根
(1) 正の数の平方根について,数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
ア 数の平方根の必要性と意味を理解すること。
イ 数の平方根を含む簡単な式の計算をすること。
ウ 具体的な場面で数の平方根を用いて表したり処理したりすること。
イ 次のような思考力,判断力,表現力等を身に付けること。
ア 既に学習した計算の方法と関連付けて,数の平方根を含む式の計算の方法を考察し表現すること。
イ 数の平方根を具体的な場面で活用すること。
〔用語・記号〕
根号 有理数 無理数 √
[内容の取扱い]
(1) 内容の「A数と式」の(1)などに関連して,誤差や近似値,a×10n の形の表現を取り扱うものとする。
[意見]
有効数字の考え方は測定器の誤差とも関連するなかなか難しい分野なので、ここで中途半端に扱うことをお勧めしません。
またどちらかというと自然科学の分野なので、中学校の理科の最後に持ってくるなど少しジャンルを変えたほうがいいと思います。
[私の考えるキーポイント]
二次方程式を扱う前に平方根が必要になるということでここであつかっているものと思います。
1)平方根とは
2乗するとその数になるものを、その数の平方根といいます。
√は根号といい、ルートと読みます。
根号を使わずに表せるときは根号を使用せず表します。
例えば 16 の平方根は
$${±\sqrt{16}=±\sqrt{2^2×2^2}=±(2×2)=±4}$$
2)平方根の計算
〇 平方根のかけ算
$${\sqrt{a}×\sqrt{b}=\sqrt{ab}}$$
〇 2乗は根号の外に出る
$${\sqrt{a^2b}=a×\sqrt{b}=a×\sqrt{b}}$$
〇 平方根の割り算
$${ \sqrt{a}÷\sqrt{b}=\frac{\sqrt{a}}{\sqrt{b}}=\sqrt{\frac{a}{b}}}$$
〇 分母の有理化:分母の根号を消す処理
$${ \frac{\sqrt{a}}{\sqrt{b}}=\frac{\sqrt{a}}{\sqrt{b}}×1}$$
$${ =\frac{\sqrt{a}}{\sqrt{b}}×\frac{\sqrt{b}}{\sqrt{b}}=\frac{\sqrt{ab}}{b}}$$
〇 平方根の足し算と引き算:根号の中が同じ数のものは同じ文字のように計算できる
$${2\sqrt{5}+3\sqrt{5}-5\sqrt{7}=5\sqrt{5}-5\sqrt{7}}$$
A(2) 簡単な多項式
(2) 簡単な多項式について,数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
ア 単項式と多項式の乗法及び多項式を単項式で割る除法の計算をすること。
イ 簡単な一次式の乗法の計算及び次の公式を用いる簡単な式の展開や因数分解をすること。
イ 次のような思考力,判断力,表現力等を身に付けること。
ア 既に学習した計算の方法と関連付けて,式の展開や因数分解をする方法を考察し表現すること。
イ 文字を用いた式で数量及び数量の関係を捉え説明すること。
〔用語・記号〕
因数
[意見]
因数分解は基本的なものだけでよいと思います。
使えるのは受験数学という箱庭か、高度に作為的に設定されたものくらいだからです。
平方完成から求められる解の公式のほうが汎用性が高く、また解の公式を無理に覚えなくてもテスト用紙にかいてあっても構わないと思います。
[私の考えるキーポイント]
始まりは分配法則になります。
$${1) ac+bc=(a+b)c [ax + bx = (a + b)x と同じ]}$$
$${2) c(a+b)=ac+bc [上の式を逆にしたもの]}$$
$${3) (a+b)c=ac+bc [かけ算は逆にしても成立]}$$
分配法則から以下のような展開公式が求められます。
$${1) (a+b)(c+d)=(a+b)c+(a+b)d}$$
$${ =ac+bc+ad+bd}$$
$${2) (x+a)(x+b)=x^{2}+ax+bx+ab}$$
$${=x^{2}+(a+b)x+ab}$$
$${3) (x+a)^{2}=x^{2}+2ax+a^{2}}$$
$${[2) の b を a に置き換え]}$$
$${4) (x-a)^{2}=x^{2}-2ax+a^{2}}$$
$${[3) の a を (-a) に置き換え]}$$
$${5) (x+a)(x-a)=x^{2}-a^{2}}$$
$${[2) の b を (-a) に置き換え]}$$
この計算を逆にして多項式の積の形にすることを因数分解といいます。
この因数分解は整式同士の割り算や二次方程式の答えを求めるときに使われる考え方となります。
A(3) 二次方程式
(3) 二次方程式について,数学的活動を通して,次の事項を身に付けることができるよう指導する。
ア 次のような知識及び技能を身に付けること。
ア 二次方程式の必要性と意味及びその解の意味を理解すること。
イ 因数分解したり平方の形に変形したりして二次方程式を解くこと。
ウ 解の公式を知り,それを用いて二次方程式を解くこと。
イ 次のような思考力,判断力,表現力等を身に付けること。
ア 因数分解や平方根の考えを基にして,二次方程式を解く方法を考察し
表現すること。
イ 二次方程式を具体的な場面で活用すること。
[内容の取扱い]
(2) 内容の「A数と式」の(3)については,実数の解をもつ二次方程式を取り扱うものとする。
[私の考えるキーポイント]
文字の次数として2が最大である方程式、二次方程式の解を求める方法は大きく3つあります。
また答えは2つ出力されます。
1)平方根による解き方
$${ 〇 2x^{2}=4 を満たすx を求める。}$$
$${ x^{2}=2}$$
$${x=±\sqrt{2}}$$
$${ 〇 (x+3)^{2}=5 を満たすx を求める。}$$
$${ (x+3)=±\sqrt{5}}$$
$${x=-3±\sqrt{5}}$$
2)因数分解で解く
展開の公式を逆に使用したり、共通する文字でくくりだす方法により実施することができます。
そこで使用される考え方は以下の当たり前にみえる考え方です。
(大切な考え方)ab=0 の時、a=0 または b=0
例えば (x+3)(x-4)=0 と因数分解できた場合、
x+3=0 又は x-4=0 となるので答えは、
x=-3 又は x=4 となります。
3)解の公式で解く
解の公式は平方完成により算出することはできます。
計算さえすれば確実に答えが分かるという点は非常に強力だと思います。
$${ ax^{2}+bx+c= の時}$$
$${ x=\frac{-b±\sqrt{b^{2}-4ac}}{2a}}$$
この記事が気に入ったらサポートをしてみませんか?
