三角関数の微分・積分の覚え方

数学III では三角関数（sin x、cos x）の微分・積分を習います。公式として表すと次のとおりです。tan x については、sin x と cos x の合成関数として考えることができるので省略します。

(1) (sin x)’ = cos x
(2) (cos x)’ = -sin x
(3) ∫ sin x dx = -cos x + C（Cは積分定数） 
(4) ∫ cos x dx =  sin x + C（Cは積分定数）  

これらの公式は、正負が入り乱れている点が覚えにくいようです。私は公式としては覚えていません。代わりに次のように覚えています。

微分は−90°回転、積分は90°回転

これだけではさすがに何のことだかさっぱり分からないと思うので、下の図を使って説明しましょう。前段として知っておいて欲しいことがあり、それは cos や sin の意味です。これについては別の note で書こうと思いますが、いまはざっくりと「cos は x 座標、sin は y 座標」ということを覚えておいてください。

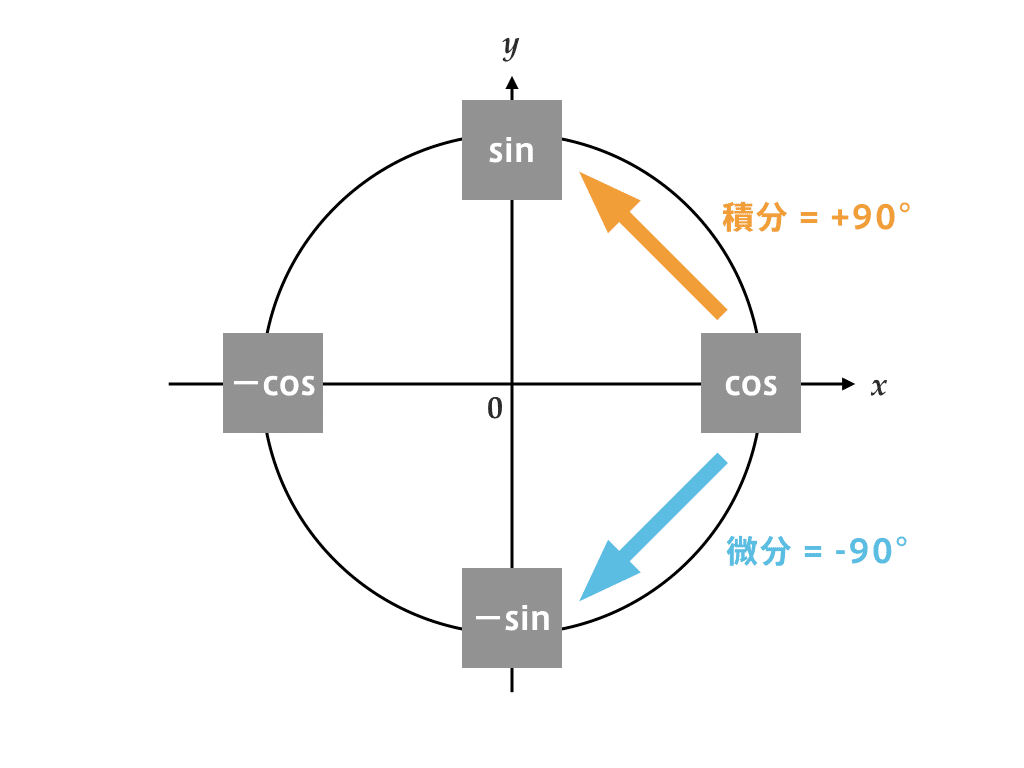
上図のように、単位円上に cos、sin、-cos、-sinを配置します。「cos は x 座標、sin は y 座標」ですから、この配置には納得できると思います。また、それぞれの軸の負の部分にあるものは「-cos」「-sin」とマイナスがつくのも納得がいくものだと思います。

この図と、さきほどの「微分は-90°回転、積分は90°回転」で cos と sin の微分・積分ができます。実際にやってみましょう。

cos x を微分しよう！
cos があるところから-90°回転させると -sin のところに来るなぁ……
じゃあ、-sin x だ！

cos x を積分しよう！
cos があるところから90°回転させると sin のところに来るなぁ……
じゃあ、sin x だ！
おっと、積分定数も忘れずに足して、sin x + C（Cは積分定数）だ！  

どうでしょうか。これならだいぶ覚えやすくなっていると思います。この方法だと、公式化されることはほとんどない -sin x や -cos x の微分・積分もすぐに答えられるようになります（まあ普通に計算するのでもよいのだけど……）。もっと便利なのは、2階微分など複数回の微分・積分が楽になる点です。気に入ったら、ぜひ使ってみてくださいね。