
ニュートン法で求めるベッセル関数の零点
Pythonを使った数値解析・アルゴリズムに関する投稿第2弾です。以下ではニュートン法を用いてベッセル関数の零点を求めるということをやっていきます。基本的な微積分の計算ができれば理解できるよう丁寧に説明していきますので、物理学と数理最適化のいずれかに関心のある方には楽しめる内容になると思います。
ベッセル関数とは古典物理学の複数の分野で現れる「特殊関数」の一種です。様々な応用先がある重要な関数ですが、いかんせん数式が複雑であるため難解なものと思われがちです。一方ニュートン法とは与えられた連続関数の導関数を用いて根(関数の値が0になる点)を求める数値解析の手法です。まずはこちらについて説明していきます。本題に入るのは5節目です。
1. 一変数関数に対するNewton法
ただ一つの(実の)変数xを持つ滑らかな関数f(x)があったとします。このような関数としては
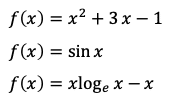
などなど色々考えられます。こうした関数の値がゼロになる点、つまり
![]()
となる解xを求めるような問題を考えます。そのようなxで表される点をその関数の零点だとか根と呼びます。一般には複数の根を持つ関数を扱うこともありますが、ニュートン法ではどこかに出発点を定めてその近くにある根を探します。
イメージしやすくするため上記3つの関数をxy平面上のグラフにしてみましょう。中央を横切っているのが y=0 の横軸で、この線と各関数の描く曲線 y=f(x)との交点を求めることがここでの目標です。

関数の値がゼロになる点を求めるというと極々特殊なケースに限った話に思えるかもしれませんが実際はそうでもありません。
まず理学・工学の応用分野では相異なる2つの関数の値が一致する点を求めたい場面がしばしばあり、それが手計算で求められないならば2つの関数をg(x)、h(x)として関数 f(x) = g(x) - h(x)の根を求めることになるからです。有名な例としては tan(x)とxの値が一致する点を探すという問題があります(以下で現れる三角関数は全て角度の単位をradとする弧度法のものです)。
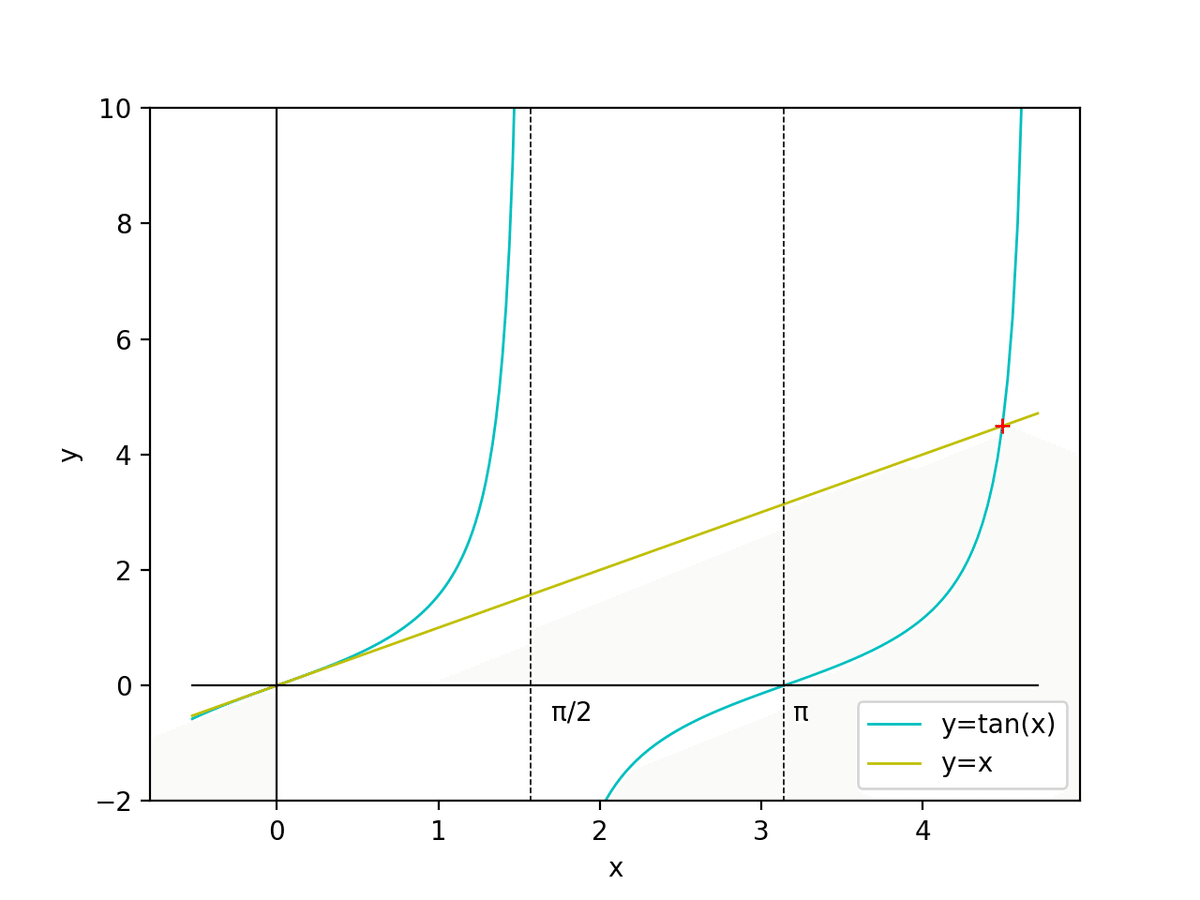
こちらがその2つの関数のプロット図です。まず原点x=0がその解であることは明白ですが、その他にも無限個の解があります。例えばこちらの図の中ではx=4.5の近くに十字で記した交点があります。この点の座標を厳密に求めることはできませんが、後述するようにニュートン法で近似的に求めることができます。
それから数値最適化の分野では、複数のパラメータを持つ関数を最大化ないし最小化する条件を探す問題をしばしば扱います。そのような関数は目的関数と呼ばれ、目的関数をそのパラメータで微分することで得られる導関数がゼロになる点を探すことになります。したがってこの目的関数の導関数にニュートン法を適用するというケースが出てきます。その時は一般に多変数関数に拡張した方法を考えなければいけませんが、今回はただ一つの変数を持つ微分可能な関数だけを扱います。
その方法を説明しましょう。曲線 y=f(x)に対し、 x = x_k (k=0, 1, 2, ... )の点における接線と横軸 y=0との交点を x = x_k+1 とします。関数f(x)の導関数をf'(x)と書くことにすると点x = x_kにおける接線の傾きはf'(x_k)であり、接線の方程式は
![]()
で表されます。少々紛らわしいですが添字の付いた x_kは変数xに依らない定数です。
左辺のyがゼロの時に xの値が x_k+1に等しくなるので
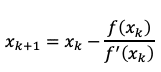
によって x_k+1 が求められます。
この操作をx_0から始めて何度か繰り返し、ある正の小さい値εについて
![]()
なる収束条件が満たされたときに、最後に求められた x_k+1を元の方程式の解とします。これが一変数の関数の根を求めるニュートン法です。最初のx_0は根に十分に近いと考えられる点を適当に決めて与えます。
文章や数式よりも図の方が分かりやすいでしょう。英語版Wikipediaには動く絵もあるのでそちらを見ると尚良いかもしれません。下のプロット図では関数f(x)=tan(x)-x について、後述するコードで x_0 = 4.6から開始して x_1, x_2等を求めています。その結果としてtan(x) = x の近似的な解 x≒4.4934にたどり着いています。
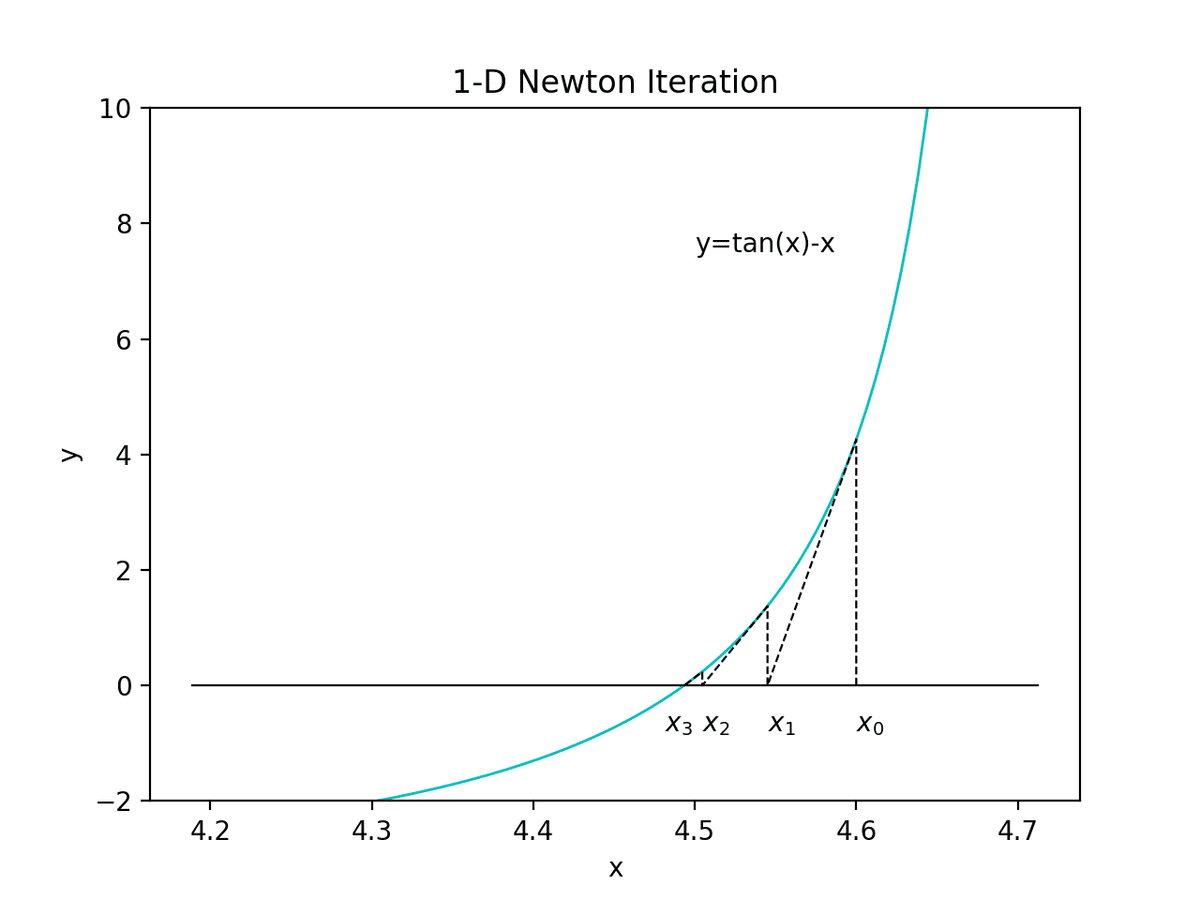
2. Pythonによる一変数のNewton法の実装
ここで一度まとめるとニュートン法の考え方の要点は次の2つです。
(1) x_0を出発点として逐次的に解に近い点 x_1, x_2, ... を求めていく。
(2) 予め定められた収束条件を満たたところで打ち切って近似解とする。
def newton1dim(f, df, x0=0.0, max_iter=1e+2, eps=1e-8):
x = x0
step = 1
x_new = x - f(x)/df(x)
while not abs(x_new-x) < eps:
step += 1
x = x_new
x_new = x - f(x)/df(x)
if step >= max_iter:
break
return [x_new, step, abs(x_new-x) < eps] このことをPython3で表したのが上記のコードです。
・fは解を求めたい連続関数
・dfはfの導関数
・x0は出発点の座標(初期値)
・max_iterは繰り返しの最大回数
・epsは収束条件のε
といったものになります。繰り返しの回数に上限を定めるのは解が求められない場合に無限ループに入るのを防ぐためです。
収束条件 abs(x_new-x) < epsが満たされてループから脱した時のx_newが求めたかった解(先ほどのx_k+1)になります。この他にも動作の確認をするために「その解にたどり着くまでのステップ数」と、「収束条件が満たされたか否か」も返すようにしています。
これを用いて f(x)=tan(x)-xの x=4.5付近の根を求めましょう。
関数f(x)の導関数は
![]()
なので、newton1dimに続けて
def f(x=0.0):
return np.tan(x)-x
def df(x=0.0):
return np.tan(x)**2-1.0といった2つの関数fおよびdfを追加します。そしてこれらと初期値x0 = 4.6 とを先ほどの関数newton1dimへ渡します。そうしてリスト型の返り値をそのままコマンドラインに表示させることで次の出力結果を得ます。
[4.493409457871261, 8, True]この結果よりx_8までが計算されて、近似解 x≒4.4934が求められたことが分かります。これが先ほど述べたtan(x)とxの値が一致する点の一つです。
さらに別の関数として
def lis1dnewton(f, df, x0, num=5, eps=1e-8):
lis = [[x0, f(x0)]]
for i in range(num):
x = lis[i][0]
x_new = x - f(x)/df(x)
lis.append([x_new, f(x_new)])
if abs(x_new-x) < eps:
break
return lisを定義しておくと、収束先の解だけでなくx_0、x_1、x_2といった途中の点と、それらに対する関数f(x)の値を出力できます。先ほどはこの出力結果lisを利用してx_0、x_1、x_2を表す点線(逐次解の軌跡)を描きました。
[補足]
ここでの実装では関数f(x)自体とその導関数f'(x)とを別々に用意しましたが、導関数の方を微分の定義に則って
def df(x=0.0, eps=1e-8):
x_new = x + eps
return (f(x_new)-f(x))/epsのようにするやり方も考えられるでしょう。しかしこれだとf(x_new)-f(x)がepsと同じオーダーのかなり小さい数になってしまい計算の精度が期待できない(桁落ちの恐れがある)ため、一般には中身の分かっている関数であれば導関数を別に与えた方が賢明とされているようです。
ここまでの内容は『機械学習のエッセンス 実装しながら学ぶPython、数学、アルゴリズム』を参考に書きました。以前著者の加藤公一さんがブログで別の本について書かれた書評を引用しましたが、それとは別にこちらの書籍も買って勉強させてもらっています。
本節の最後に、例として最初に挙げた3つの関数
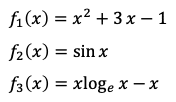
に関する結果も挙げておきます。区別のため番号を付けました。それぞれの導関数は次の通りです。
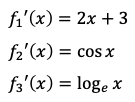
まずこれらを定義します。
def f1(x=1.0):
return x**2+3*x-1.0
def f2(x=1.0):
return np.sin(x)
def f3(x=1.0):
return x*np.log(x)-x
def df1(x=1.0):
return 2*x+3.0
def df2(x=1.0):
return np.cos(x)
def df3(x=1.0):
return np.log(x)
xini = [0.7, 2.4, 3.1]最後のxiniはそれぞれの関数の根を求めるためのxの初期値(initial value)を集めたリストです。これらの関数と初期値を先ほどのnewton1dimへと渡して得られた根をグラフの中にプロットしてみます。

緑色の十字印が各関数に対するx の初期値と、その点における関数の値を示しています。これに対して赤色の十字がニュートン法で求められた根です。それぞれの値もグラフ内に書き込みました。
ちなみにf1は2次関数なのでその根は2次方程式を解くことで
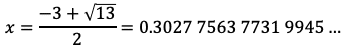
と求められますし、f2のx=3近くの根といえば円周率
![]()
に他なりません。比べてみると上記の結果はこれらの値に、少なくともepsより小さい誤差のみを残して一致しています。
3. 整数次の(第一種)Bessel関数
ベッセル関数とは冒頭で述べた通り古典物理学の複数の分野で現れる特殊関数です。これから説明するように何をその定義とするかには複数の流儀があります*1。
歴史的には関数の名前にも名を残している天文学者Friedrich Wilhelm Besselが、今日の高校物理の教科書にも登場する「ケプラーの法則」に従う惑星の運動について解析的に解いた際に初めて見出されたとされます。その帰結の一部を現代的な表記で書くと、

という積分が惑星軌道に関する微分方程式の解の中に現れます*2。これがn次の(第一種)ベッセル関数と呼ばれるもので、整数nは次数と呼ばれます。
[補足]
*1 これを知らないで本などを読むと初学者は困惑することになります。
*2 この導出についてWeb上では例えば「Scientific Doggie 数理の楽しみ」というサイトにあるこちらのPDFで見ることができます。
http://www.wannyan.net/scidog/spfunc/ch03.pdf
一見すると①は三角関数の中に三角関数が入るというとんでもない代物に見えます。この積分を計算しようとは思わないで、代わりに両辺をxで微分した上でxをかけるという操作をします。
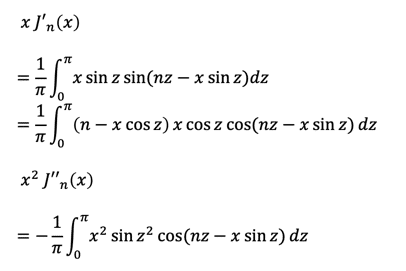
途中で一度部分積分を行っています。次にこれらを足しあわせます。
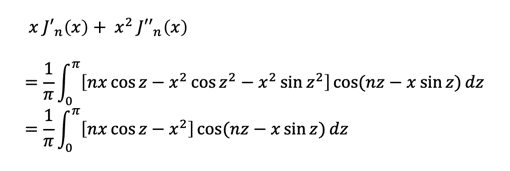
そして天下り(業界用語)になりますが、
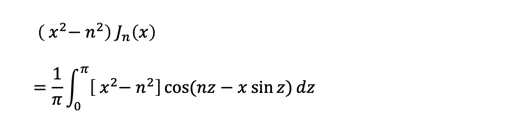
なるものを両辺へと足し、t = nz - x sin(z)で置換積分を行います。

はい、というわけで先ほど導入した関数J_n (x)の正体を知ることなくこの関数が
![]()
なる方程式(ベッセルの微分方程式)を満たすことが分かりました。
積分による定義の式①とは別に上記の方程式の解をべき級数展開と呼ばれる方法で求めることもできます。ただしその文脈では上記の微分方程式を満たすことに加えて「原点 x=0において(発散することなく)正則であれ」という条件が付きます。その解の求め方については市販の教科書類や講義ノートなど様々なところで詳しく説明されています。なのでここでは結果のみ書きます。それはこういうものです。

これは先ほどのベッセルの微分方程式の解になっているだけでなく、一見すると先ほどと全く似つかない表式ですが①の積分と一致します。
この関数J_n (x)の集まり(関数列){J_n (x)| n =0,1,2,...} には母関数として

があります。これの意味するところは、xの値を固定しtについて左辺を級数展開すればtのn乗にかかる係数がJ_n (x)になるということです。これは複素関数論を通じて証明されます。
これまで登場したベッセル関数の表式を改めて列挙します。

まず①のように特殊関数を別の変数による積分の結果として表したものをその関数の積分表示といいます。先ほど述べたように歴史的に初めて見出されたベッセル関数はこの形式でした。
一方で今日の多くの本や講義ノートでは②の冪(べき)級数展開をベッセル関数の定義としています。これは積分表示の式と別物のように見えますが、③の母関数を通じて互いに等しいことが示されます。
そのため(こちらのPDFファイルのように)むしろ③をベッセル関数の定義だとして①②やその他諸々の関係式を示す流儀があります。そうすると不自然さや曖昧さの取り除かれて首尾一貫した議論ができます。
またここまでnを整数としてきましたが、より一般的にはこれを実数、さらには複素数のパラメータへと拡張してベッセル関数を定義することもできます。その場合上記②の式の分母は階乗ではなくガンマ関数になります。
さらにベッセルの微分方程式の解としてはこの他に原点で正則でなくなる(おおよそ1/√xに比例して発散)する解があり、それをノイマン関数といいます。あるいはベッセル関数J_n(x)とノイマン関数をまとめて「ベッセル関数」と称し、前者を第1種、後者を第2種と呼ぶこともあります。
しかしここで徒らに一般化しても特に意味はないので、本投稿では引き続きnが整数であるとして第1種ベッセル関数J_n(x)のみを扱います。かなり後の方で述べるように整数次の(第1種)ベッセル関数にはその零点を求めることに実用的な意味があり、かつそれが手計算で求められないという性質があります。いち数理物理学ファンとしては、ニュートン法を知ったときにこれを使って自分でもベッセル関数の零点を求めてみようと考えたのでした。
4. Pythonによる整数次Bessel関数とその導関数の実装
それではベッセル関数をPython3で実装します。ここでは②の級数表示を利用します。本来は無限個の項からなる級数ですが整数型の変数numで指定した個数の項で打ち切ります。
# Bessel functions of the first kind in limited series expansion
def funcjn(x=0.0, n=0, num=25):
y = 0.0
if n >= 0:
for m in range(0, num+1):
coef = (-1)**m
demon = factorial(m)*factorial(m+n)
vari = (x/2)**(2*m+n)
y = y + coef*vari/demon
else:
y = (-1)**n*funcjn(x, -n, num)
return y分母にある階乗関数factorialはmathライブラリからimportするか、以前再帰的プログラミングの例として紹介したように
def factorial(n=1):
if n<=1:
return 1
else:
return n*factorial(n-1)として自分で定義します。
果たしてこれで正しく実装できているのか調べるためにmatplotlibライブラリを利用してプロットしてみます。変数numはデフォルトの25としていますので無限級数の中の初めの26個の項による近似です。

これだけ見ると「ベッセル関数」で検索して出てくるグラフと同じように見えます。この後で今回の本題である零点、つまり横軸との交点の座標を求めることで再度正確に計算できているか確かめます。
関数J_n(x)はその定義より、遠方(x>>1)において漸近的に
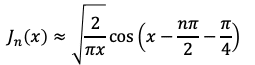
となることが示されます。しかし下のグラフのように上記の有限個の項による近似ではxがある程度大きいところで発散し始めてしまいます。ここではnum=25としたままプロットの範囲だけを広げてみました。この結果から正確な値の欲しい区間やパラメータnの値次第では計算する項の数を増やすか別の実装を考える必要があることが分かります。

ニュートン法で計算を行う前には関数 J_n(x)の導関数も導入すべきでした。それは次のように行います。まず式②より n≧0について
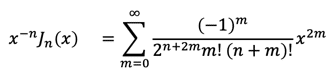
です。この両辺をxで微分してみると、右辺においてm=0の項が消えることに注意して

が成り立つことが分かります。途中で k=m-1に置き換えました。この両辺へxのn乗を乗じて
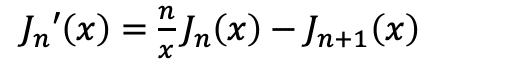
なる微分の公式を得ます。つまりベッセル関数の導関数が次数nの異なるベッセル関数との差分で表されるということです。
def dfuncjn(x=0.0, m=0, num=25):
return (m/x)*funcjn(x, m, num)-funcjn(x, m+1, num) これを利用してPythonでは関数 J_n(x)の導関数として上記の関数dfuncjnを実装しておきます。これで本題へ進むための道具立てが揃いました。
余談ですがこの他に母関数③の両辺をtやxで微分することで
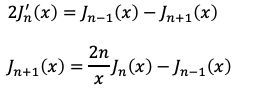
といった漸化式を導くことができます。これらは教科書や演習書に載っています。第2式では次数nを下げることができます。次数nが大きい場合には左辺を先ほどのfuncjnのような有限個の項の直接計算で近似するよりも、右辺に着目して前回直交多項式を再帰的手法で実装したときのように次数nの小さいベッセル関数の差分とする方が精度は良いかもしれません(これは未検証です)。
5. Newton法で求めるBessel関数の零点
以上はニュートン法とベッセル関数それぞれの導入(イントロダクション)でありここからが本題です。
まず、必要な関数のコードを再掲します。
# Bessel functions of the first kind in limited series expansion #
def funcjn(x=0.0, n=0, num=25):
y = 0.0
if n >= 0:
for m in range(0, num+1):
coef = (-1)**m
demon = factorial(m)*factorial(m+n)
vari = (x/2)**(2*m+n)
y = y + coef*vari/demon
else:
y = (-1)**n*funcjn(x, -n, num)
return y
# Derivative of Bessel functions #
def dfuncjn(x=0.0, m=0, num=25):
return (m/x)*funcjn(x, m, num)-funcjn(x, m+1, num)
# Factorial of a positive integer #
def factorial(n=1):
if n<=1:
return 1
else:
return n*factorial(n-1)# Method #
def newton1dim(f, df, x0=0.0, n=0, eps=1e-10, max_iter=1e+2):
step = 1
x = x0
x_new = x - f(x, n)/df(x, n)
while not abs(f(x_new, n)) < eps:
step += 1
x = x_new
x_new = x - f(x, n)/df(x, n)
if step >= max_iter:
break
return [x_new, step, abs(f(x_new, n)) < eps]ここでxの初期値x0と次数nを指定した上で
sol = newton1dim(funcjn, dfuncjn, n, x0)とすることで解のリストsolを取得できます。第2節と異なり関数funcjnの引数に不動小数点型のxの他に整数型のnがあるためnewton1dimでもnを扱うようにしました。
リストsolの各要素はそれぞれ
sol[0] :ニュートン法で求められた初期値x0近くの根
sol[1] :それに至るまでのステップ数
sol[2] :収束条件が満たされたか否か
を意味します。
例として n = 0、x0 = 5.4として計算させた結果を、solをそのままコマンドラインに出力させることで確かめてみます。
[5.520078110286313, 3, True]この結果の意味するところは次の通りです。
初期値x = x0から始めて「x_new = x - f(x, n)/df(x, n)」という代入を3回行なったことで「x_new-x の絶対値がeps=1e-10より小さい」という収束条件を満たす根 x≒5.52が求められた。
この結果をプロットしたのが下のグラフです。シアン色の曲線が次数n=0のベッセル関数J_0(x)、緑色のマークが初期値x0の位置を、赤色のマークが根を表します。

今回の条件では上手く行きましたが、初期値の取り方次第で計算は失敗します。例えば上記のJ_0(x)の場合 x≒7.07が極(導関数がゼロになる点)であるため、この近くに初期値 x0を取れば接線がほぼ真横を向いてしまいます。そうなると関数funcjnがベッセル関数を十分に近似できてる区間内で接線が横軸に交わらないため収束条件を満たす根に到達しません。
また、先述の通り関数funcjnは有限個の項による近似でありxが20を超えるあたりで本物のベッセル関数と明らかに異なる挙動を始めます。そのような変域に初期値x0を取ると次のようになります。

[115.8601597857589, 100, False]こちらは次数 n=3、初期値 x0=21.0、ベッセル関数の近似の次数 num=25 (デフォルト値)での計算例です。このあたりではfuncjnだけでなくdfuncjnの形も崩れてしまい100回の代入計算を行っても収束条件が満たされることなくx=19.4付近の根に到達できませんでした。
続いてただ1つの根を求めるだけでなく、同時に複数の根を求めてベッセル関数の零点の表を作成します。そのためにまず根を探す出発点の値を載せたCSVファイル sample_data.csvを作成します。
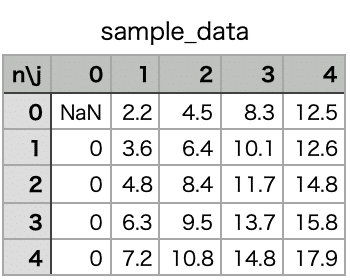
MacOS標準のアプリNumbersでCSVファイルを開いた様子です。一番左の列でベッセル関数の次数nを指定しています。その次の列は原点の座標で、n=0以外ではここが自明な零点(*)になっています。そこは0番目の零点として素通りし、その次の列から各次数のベッセル関数の零点を求める初期値を書き込んでいます。これらの値は下のようなプロット図を見ながら目分量で選びました。

*補足
級数展開式②より、原点x=0の近くでベッセル関数J_n(x)はxのn乗の定数倍に近似されます。
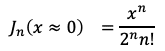
この表式からも分かるように次数nが0でなければ原点において J_n = 0となります。しかしnが2以上であれば原点x=0の近くで J_n(x)自身だけでなくその導関数も0に近づいてしまい、ニュートン法の代入式
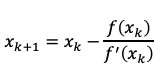
右辺第2項がうまく計算できません。そのため x=0が零点であることは明らかなのに数値計算ではなかなかそこに到達しないということが起こります。そのためここは「自明な零点」として飛ばします。
Pythonではsample_data.csvの0列目の次数nと2列目以降の初期値x0をreadした上でnewton1dim(funcjn, dfuncjn, x0, n)で根を計算し、新しいCSVファイルresult_data.csvを作って結果をwriteします。このとき比較しやすいよう最初の行と第0列・第1列をsample_data.csvからコピーしておき、各々の根を求めるのに使った初期値がsample_data.csvにおいて入れられていたのと同じ位置に根の値を書き込んでいきます。
[処理の流れ]
(0)開始 # 使用するライブラリ、関数のimport
(1)CSVファイル"sample_data.csv"を読み込んで各要素を2次元のリストdata_csvに保存する。
(2)空のリストresultsを定義する。
(3)目次になっている0行目を飛ばし、1行目から最終行までにおいて次の操作を行う。
・空のリストlisを定義する。
・j=2列目から最終列まで次の操作を行う。
・data_csvの0列目を整数型に変換して変数nに代入する。
・同j列目の要素を不動小数点型に変換して変数x0に代入する。
・res = newton1dim(funcjn, dfuncjn, x0, n)を計算する。
・根res[0]をlisに追加する。
・lisをresultsに追加する。
(4)新しく"result_data.csv"を作成する。
(5)data_csvの0行目をresult_data.csvに書き込む。
(6)data_csvの0列目と1列目をresult_data.csvに書き込む。
(7)resultsの各要素をresult_data.csvに書き込んでいく。
(8)終了 ここでも引き続きnum=25として、出力値は全て小数点第4位までで丸めます。計算を実行し上記のsample_data.csvから以下の出力結果を得ました。
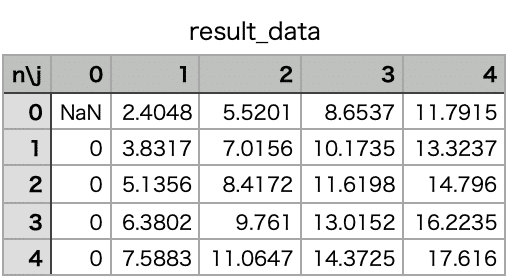
特殊関数関連の書籍やネット上の資料(例えば先ほど挙げたPDFファイルの25ページ目にある「表 3.1」)と比較すると、この範囲では根が上手く求められていることが分かります。
表題の内容は以上になります。この先では続きとしてベッセル関数の物理学への応用などについて述べていきます。厳密さや詳しさよりも一般的な書籍の行間を埋めることを重視した説明がメインになります。
冒頭に「Pythonを使った数値解析・アルゴリズムに関する投稿第2弾」と書きましたが、その第1弾は再帰的プログラミングと直交多項式に関する上記の投稿でした。こちらでも大学の物理学科で学ばれている特殊関数をPythonで実装していくつかのデモンストレーションを行っています。興味のある方は後ほどこちらもご覧下さい。
6. Helmholtz方程式とBessel関数
ベッセル関数の応用先についてきちんと説明するには円筒座標系の座標の取り方を避けては通れません。ここではそのことから説明します。
座標の取り方とはつまるところ空間内の点の位置を何らかの数の組み合わせで表す方法です。まず基準となる原点Oを決め、任意のPがOから見てどこにあると言い表すかを考えます。
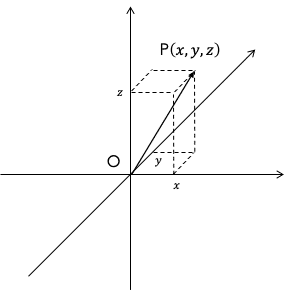
3次元ユークリッド空間での座標の取り方で、最も分かりやすいのはこの図のような直交座標系 (x, y, z)でしょう。前後上下左右の方向にx, y, zの3本の軸を取り、点Pの位置がそれぞれの軸の方向に原点Oからどれだけ離れている(変位している)かを表します。
仮にxy平面を地面だと考えてy軸正の方向を真北とするならば、直交座標系の各座標変数はそれぞれ
x: 点Pが原点から見て東へどれだけ変位しているか
y: 点Pが原点から見て北へどれだけ変位しているか
z: 点Pが原点から見て真上へどれだけ変位しているか
といったことを数値で表します。点Pが原点より西、南、下にある場合にはそれぞれx、y、zが負になります。
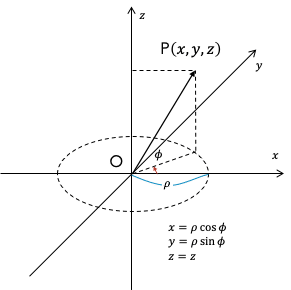
これに対して円筒座標系 (ρ, φ, z)とはzだけをそのままに、xとyの指定の仕方を変えた座標の取り方です。直交座標系の変数との関係は上の図の通りです。先ほどと同様の説明をするならば、ρ(ロー)とは「点Pから真っ直ぐに垂線を下ろして地面へ達したところの点と原点Oとの距離」であり、φ(ファイ)は「その点まで原点から引いた直線が真東の方角からどれだけ回転しているか」を表します。その意味合いゆえρは動径、φは方位角とも呼ばれます。先ほどのx、y、zが正にも負にもなるのに対し、円筒座標系のρは0または正、φは0から2π(ラジアン)の範囲に限られます。
この座標の取り方を採用するのは、円筒形状の管の中を伝わる電磁波や流体だとか、円柱型の物体内を伝わる熱などを扱うケースです。いずれも中心に一本の軸があると考えてそれをz軸とします。
こういった問題で電磁場、電流密度、温度分布などの従う方程式を立てたとしましょう。そこへさらにいくつかの基本的な要請をすれば多くの場合に

という形のヘルムホルツ方程式へ帰着させることができます。この式の中にある三角形の記号は(3次元の)ラプラシアンと呼ばれる偏微分演算子の記号で、もしuを直交座標系のx、y、zの関数とするならば
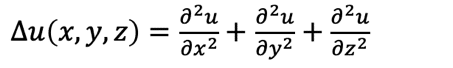
であり、円筒座標系のρ、φ、zの関数とするなら
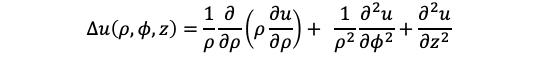
が成り立ちます。
もしuが常に0であれば微分しても別の数をかけても0のままなので上記の方程式は成立しますが、それは自明な解と呼び普通はそれ以外の解を探します。そしてその解は電磁場、電流、温度といった量の分布を表します。
[補足]
よく〇〇座標系でのラプラシアンを求めるという証明問題があって大抵は偏微分の演算子だけを書きますが、大前提として微分演算子は何らかの関数に作用して初めて意味を持つもので、その関数がどんなものであっても恒等的に等号が成り立つから関数を省略して書いていることに注意が必要です。
敢えて直交座標系ではなく円筒座標系を選択する場合、そこには明白な意図があります。
ヘルムホルツ方程式のような微分方程式には一般に無数の解が存在し、それらをまとめて一般解と呼びます。これに対して実際の1つの物理現象を記述する解があるとするならそれらの解の中の一つになりますが、どの解が選ばれるかを決定するのは微分方程式ではありません。基準となる時刻における状態を指定する初期条件や、関数が定義される区間の端(例えば円筒形状の容器の壁面)などで未知関数が満たす境界条件です。
円筒座標系が採用される場合、典型的には動径ρがある特定の値aになる点において
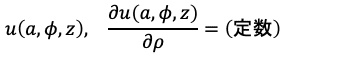
という形の境界条件が付きます。例えば電磁波が円筒形状の管(導波管)の内側に閉じ込められていると考える場合には境界となる壁面でこのような条件が適用されたように思います。もしここで直交座標系のx, y, zに拘っていれば先ほどの境界条件が
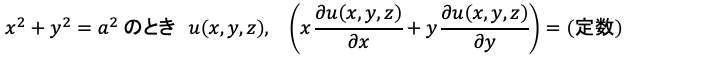
とややこしくなってしまいます。それではなかなか話が進まないので普通は円筒座標系を使います。
せっかくなのでそのような場合のヘルムホルツ方程式の解を求めてみましょう。まず円筒座標のρのみに依存するf、φのみに依存するξ(グザイ)、zのみに依存するγ(ガンマ)の3つの因子によって関数uが
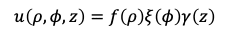
のように分けられると考えます。これを円筒座標での変数分離といいます。このようにすると、特に上記の境界条件で右辺の定数が0であれば
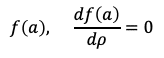
の如く簡潔に書くことができます。
変数分離型の解 u(ρ, φ, z) = f(ρ)ξ(φ)γ(z)を仮定するとヘルムホルツ方程式はこのようになります。
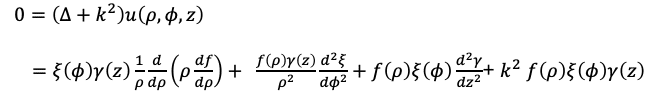
今は関数uが0でないとしているので両辺に1/u = 1/(fξγ)をかけて
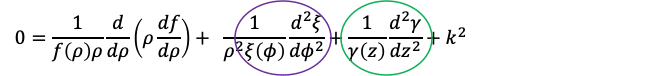
とします。ここで各項に注目すると1つ目は動径ρのみに依存し、2つ目はρのマイナス2乗が掛かっていることを除けばφのみに、そして3つ目はzのみに依存していることが分かります。3つの座標変数 (ρ, φ, z)は互いに連動することなく互いに独立に変化するものなので、この等式が成り立つためには2つの丸で囲った部分が一定でなければいけません。
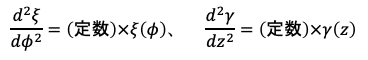
ここでξ(φ) の変数φの性質を考えると、φ=2πで一周してx軸正の方向(真東の方角)φ=0に戻るわけですから
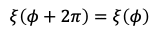
となっている必要があります。これも解を決めるのに必要な境界条件の一つです。これら微分方程式と境界条件の両方を満たすのは
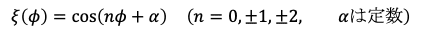
なる関数です。
一方でγ(z)にこれと同じような条件は付きませんので
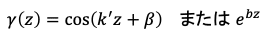
のような解が考えられるでしょう。この中に含まれるk'、β、bはいずれも座標と無関係な定数です。後者は単調に減少ないし増加する関数であるので、z→±∞となる遠方で際限なく大きくなっていくのを許容しない限りは前者のような三角関数だけが採用されます。
そこでこれらの解

を先ほど丸印で囲ったところへ代入することで
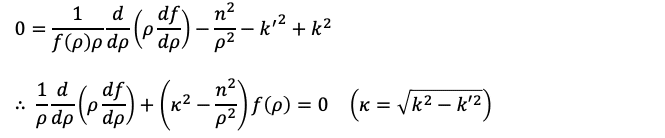
となります。ここで導入した新しい定数κはカッパと読みます。これが0ではないと仮定して、x=κρという変数変換を行います。このxは直交座標系のxとは別物であり、次元解析をすれば分かるように無次元量です。
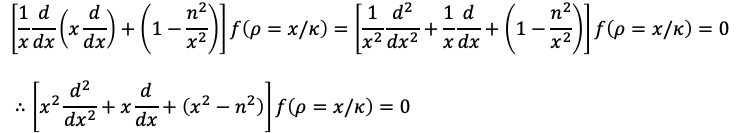
これはベッセルの微分方程式
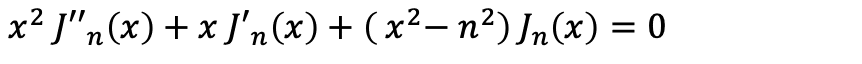
に一致します。したがって関数f(ρ=x/κ)はベッセルの微分方程式を満たし、先ほど少し述べたように原点 ρ=0において正則であるならばベッセル関数J_n(x=κρ)の定数倍になります。このような性質からベッセル関数、先ほど名前だけ出したノイマン関数、そしてそれらの線形結合をまとめて円筒関数と呼ぶことがあります。
ここまでの議論をまとめるとヘルムホルツ方程式
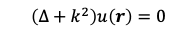
の解が次の形に定まることが分かりました。
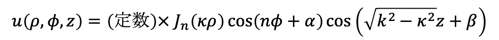
全体にかかる定数や各関数の中に含まれる n、κ、α、β、といった定数はいずれも境界条件によって定まります。もしその中で先ほどの u(ρ=a, φ, z) = 0なる境界条件があれば、
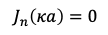
という方程式を解くことで定数κの候補が求められることになります。そのためベッセル関数の零点を求めることは純粋に数理物理学的な興味だけでなく応用上の必要性もある問題になります。これでようやく今回の主題の意義に触れられました。
上記の関数u(ρ, φ, z)で表され得る量としては、円筒型の管の内部を伝播する電磁波の成分、円柱型の物体内の温度分布、円筒型の容器の中に閉じ込められた粒子のシュレーディンガー方程式の解が挙げられます。
もしその管や容器が円筒形状でなく直方体であった場合には例えば
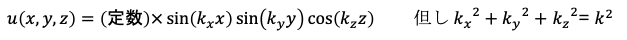
のように関数uは三角関数だけで表すことができるでしょう。一般解はx, y, zそれぞれの三角関数の積と和(線形結合)になります。具体的な解に含まれるのがsinなのかcosなのか、振幅はいくらか、そして(k_x, k_y, k_z)の各成分の値はどうなるかといった事柄は詳細な境界条件によって定まります。
このこととの対比から、ベッセル関数(一般には円筒関数)は円筒座標系において直交座標系の三角関数と同じ役割を担うとも言われます。もう少し詳しく言うと円筒座標系の変数ρの関数を展開する「基底」になるということです。基底とは任意の関数をあるルールに従って分解した時の構成要素に関わるもので、最低限の条件を満たすあらゆる関数がその組み合わせで表されます。
実はヘルムホルツ方程式の解でなくても同じ領域内で定義される区分的に連続な関数であれば同様に三角関数の組み合わせで表すことができます。それをフーリエ級数展開といいます。最低限の条件を満たす限りは任意の関数が無限個の三角関数の積や和で表すことができて、一つ一つの三角関数がその展開式における基底を構成します。直交座標系から円筒座標系に移って同様のことを考えるとき、三角関数が持っていた基底の役割はどのような関数が担うだろうかと問えばその答えがベッセル関数だということです。
7. 三角関数、Bessel関数、球Bessel関数の比較
前節では3次元の直交座標系と円筒座標系を対比して説明してきましたが、この他にも常用される座標系に球面座標系(もしくは球座標系、3次元極座標系)があります。そして球面座標系ではベッセル関数に類似する「球ベッセル関数」が導かれます。直交座標系の三角関数、円筒座標系のベッセル関数、そして球面座標系における球ベッセル関数を対比することで本投稿を締めくくりたいと思います。
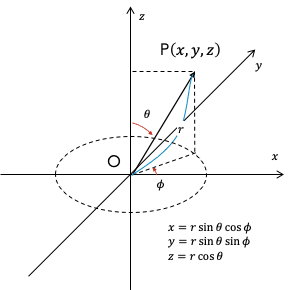
球面座標系 (r, θ, φ)では直交座標系のx、y、zが全て置き換わります。変数間の関係は上の図に書かれた通りです。この中で動径rとはシンプルに原点Oから点Pまでの距離であり0または正の値を取ります。2つある角度の変数のうちθ(シータ)はz軸正の方向(天頂方向)からどれだけ降りた角度に点Pが位置するかを意味します。このことからθは天頂角とも呼ばれ、その値は半周分つまり0からπ(ラジアン)の間に限られます。そしてφは円筒座標系のそれと同じく、点Pから真っ直ぐに垂線を下ろして地面へ達したところの点がx軸正の方向からどれだけ回転しているかを表しており、やはり方位角と呼ばれていて0から2π(ラジアン)の範囲に限られます。
そしてuを球面座標系のr、θ、φの関数であるとするとき、
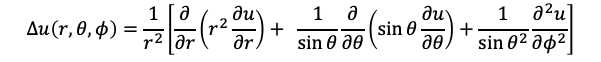
となります。この「球座標のラプラシアンの導出」は物理学科の伝統行事の一つです。
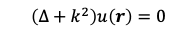
ここで再びヘルムホルツ方程式を考えますが、ここからは先ほど以上に話をショートカットします。未知関数 u(r, θ, φ)を
![]()
のように動径rに依存する部分とそれ以外とに変数分離します。このような解を考えるのは逆2乗力のポテンシャルがあるとか球対称な境界条件が課されているといったケースです。
先ほど円筒座標系について行なったのと似た議論から動径座標の関数 R(r)、天頂角と方位角の関数Y(θ, φ)がそれぞれ
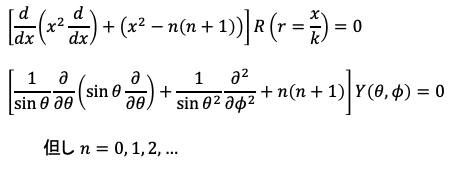
なる方程式を満たすことが示されます。この中のxとは先ほどと同じく無次元量に変換された動径rであり、直交座標系のxとは別物です。そして角度の座標変数θ、φの関数Yは3次元球面調和関数になります。
ここでさらに関数 R(r)が原点 x=0で正則であることを要求すると、上記の方程式の解は整数次の(第1種)球ベッセル関数
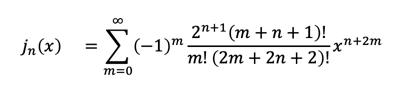
の定数倍ということになります。特に次数n=0の場合は
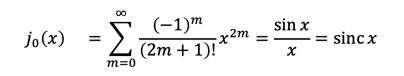
となっていわゆるsinc 関数に一致します。この他の次数についても
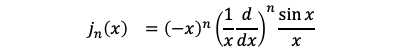
が成り立ちます。
先ほどの級数展開の式を利用し、前節のfuncjnと同様に「有限個の項の和で整数次の球ベッセル関数を近似して出力する」という関数sphejnを以下のPythonのコードで実装しました。
def sphejn(x=0.0, n=0, num=25):
y = 0.0
for m in range(0, num+1):
coef1 = (-1)**m/factorial(m)
coef2 = 2**(n+1)*factorial(m+n+1)/factorial(2*(m+n+1))
vari = x**(2*m+n)
y = y + coef1*coef2*vari
return yここで特に次数n=0とした球ベッセル関数 j_0(x)と、次数n=1のベッセル関数J_1(x)、それに三角関数sin(x)それぞれの概形を比較してみます。

上から
・Numpyライブラリのsin関数
・自作の関数funcjnを利用して出力した1次のベッセル関数
・自作の関数sphejnを利用して出力した0次の球ベッセル関数
のプロット図です。大文字のJはベッセル関数、小文字のjは球ベッセル関数を表します。いずれの曲線も上下に振動していますが、見ての通りその振れ幅の変化の仕方は互いに異なります。
これに続けて
![]()
といった関数を同じ区間でプロットしてみます。
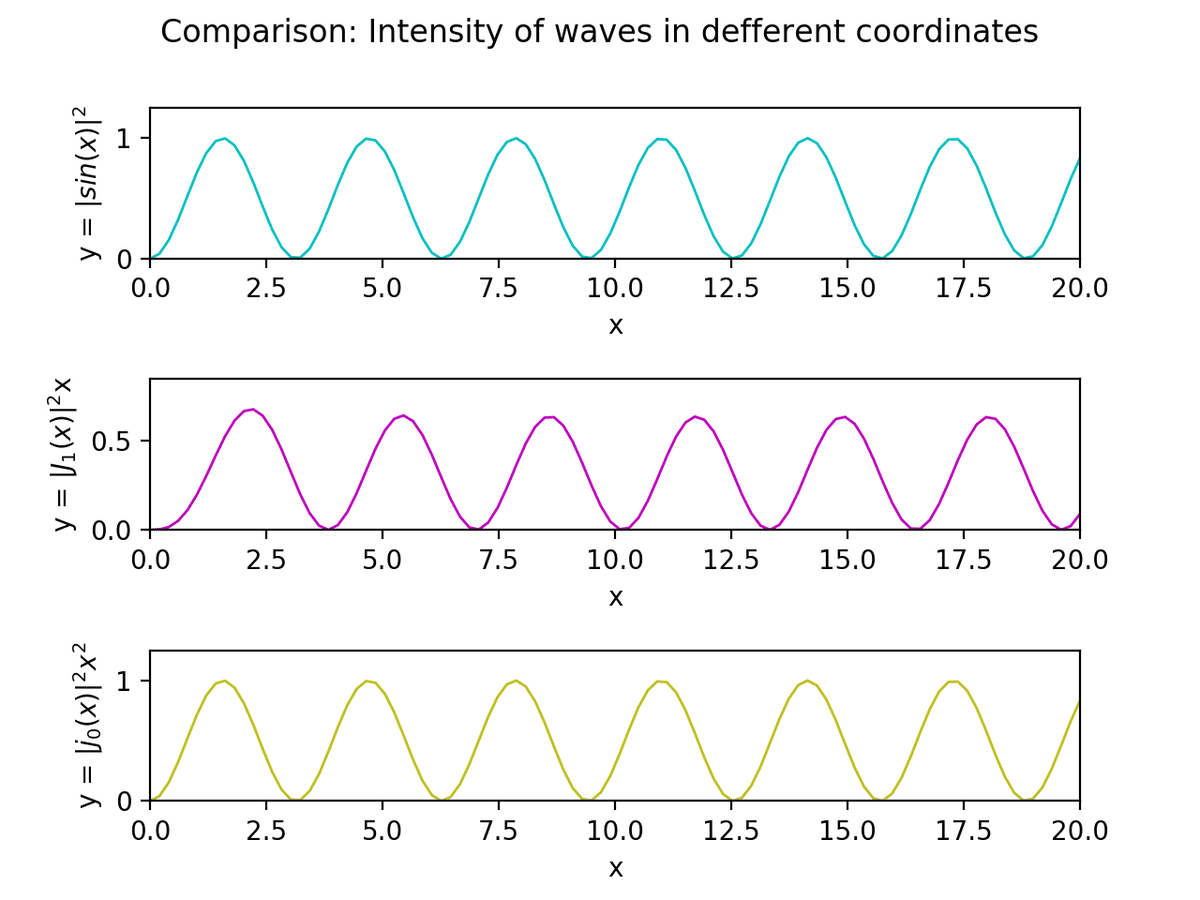
このように先ほどと比べて互いにかなり似た形の曲線が描かれました。ここからも分かるように3種類の関数の遠方 (x>>1)における振る舞いには
・三角関数の振れ幅はどこまでも一定である。
・ベッセル関数は1/√xに比例して減衰していく。
・球ベッセル関数は1/xに比例して減衰していく。
といった特徴があります。
実はこれらのプロット図の違いにはこれらの関数の物理的な意味が現れています。
ここまで
・直交座標系では三角関数が、
・円筒座標系ではベッセル関数が、
・球面座標系では球ベッセル関数が
ヘルムホルツ方程式の基本的な解になるという話をしてきました。
ヘルムホルツ方程式が現れる分野の例として電磁気学を考えると、三角関数・ベッセル関数・球ベッセル関数それら自体に比例することがあるのは電場E、磁場Bの各成分です。正確には電磁場の中でも電荷・電流・磁気モーメントによって生じる静電場・静磁場ではなく、真空中の電磁波の振幅を指します。これらはベクトル量であり一般に異なる座標系を選べばたとえ同一の電磁場を記述するにしても各成分の関数型は異なってきます。
一方その後の図でプロットしたのは電磁場の持つエネルギーを求める式
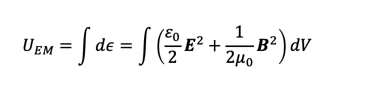
における被積分関数
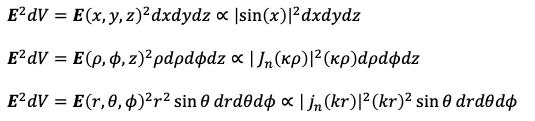
に相当します。ここでは電場Eしか書いていませんが磁場Bについても同様です。こういった量は電磁場のエネルギー密度を表していて、特に上記式は単一の波長を持つ電磁波を表す自由場の解に相当するので原点の近くでも遠くでも減衰しないで分布することになります。
最後のプロット図で3種類の曲線がいずれも減衰ないし増幅しないで一定の振幅で上下動するように見えたのはこのことと関連しています。もちろん単一の三角関数・ベッセル関数・球ベッセル関数で表される電磁波はそれぞれ別のものなので、それらのエネルギー密度の分布の形が一致することはありません。それでも基本的な振る舞いは互いに似ています。
このような性質からもベッセル関数は円筒座標系において、球ベッセル関数は球面座標系において直交座標系の三角関数のように位置付けられるとされます。特に第1種と呼んだ関数J_n(x)、j_n(x)はそれぞれの座標系でsin関数に対応すると言われるため、上の図ではsinと比較しました。
これに対してここまで触れてこなかった第2種ベッセル関数(もしくはノイマン関数)、および第2種球ベッセル関数(もしくは球ノイマン関数)はcosに対応します。これらは原点において発散してしまうように見えて、やはり第1種の関数と同じく2乗してxないしx^2を乗じてみればcosの2乗に似て見えるはずです。
8. 終わりに
以上の内容は基本的に私自身が今からちょうど10年前に大学で習った内容を昨年から勉強していることに結びつけてまとめたものでした。
ここまで書いてきて印象的だったことは大きく分けて次の2つです。第一にやはり学生の頃には学ぶべき事柄に対して勉強時間が根本的に足りなかったために理解・習得していない項目が大変多かったということです。そして第二には当時どうしても納得できないとか到底理解できないように思ったことでも、落ち着いてやり直すうちに途中であっけなく疑問が解消してしまったことです。学業では往々にしてあることかもしれませんが、「分からない」と思ったときに手を止めてしまうのではなく「分からないからこそ」学び続けることが重要なのだと改めて実感しました。
本投稿では1変数関数に対するニュートン法と整数次の第1種ベッセル関数などについて解説し、デモンストレーションとしてベッセル関数の零点を求めました。計算に必要なコードを記載しましたのでMatplotlib等を使用できる環境であればコピーして同様の計算やプロットを試すことができます。最後まで読んでいただきありがとうございました。
