
【ネスペ3問】経路計算(ネットワークスペシャリスト)
このNoteでは、ネスペR06~H21から経路に関する計算問題を集めました。
ネットワーク回線は、道路と同じで網目のよう。車と同じで、通信パケットもループがあれば迷いますし、距離や渋滞を考慮してルート選択をします。
今回集めた3問は、1問は最新R06に初登場、他2問は4回出題している常連です。たった3問ですし、ちょっと考えればすぐ解けるので、対策しておきたいですね。
なお私の全てのNoteは、学生時代の独学合格体験、大学・IT専門学校での授業経験に基づいています。少しでも信用して頂けたら嬉しいです。
それでは始めましょう!
\私の3ヶ月の学習記録/
スパニングツリーを作る計算問題
スパニングツリーは、ネットワークのループを解消するプロトコル。
ネットワークは複雑で網の目のようなので、必ずループは生じます。パケットがループを巡回するといつまで経っても届きません。
スパニングツリーでは、良い回線を採用して、ループの原因になる不要な回線への接続口(ポート)を使用不可に設定します。>STPのNote(準備中*)
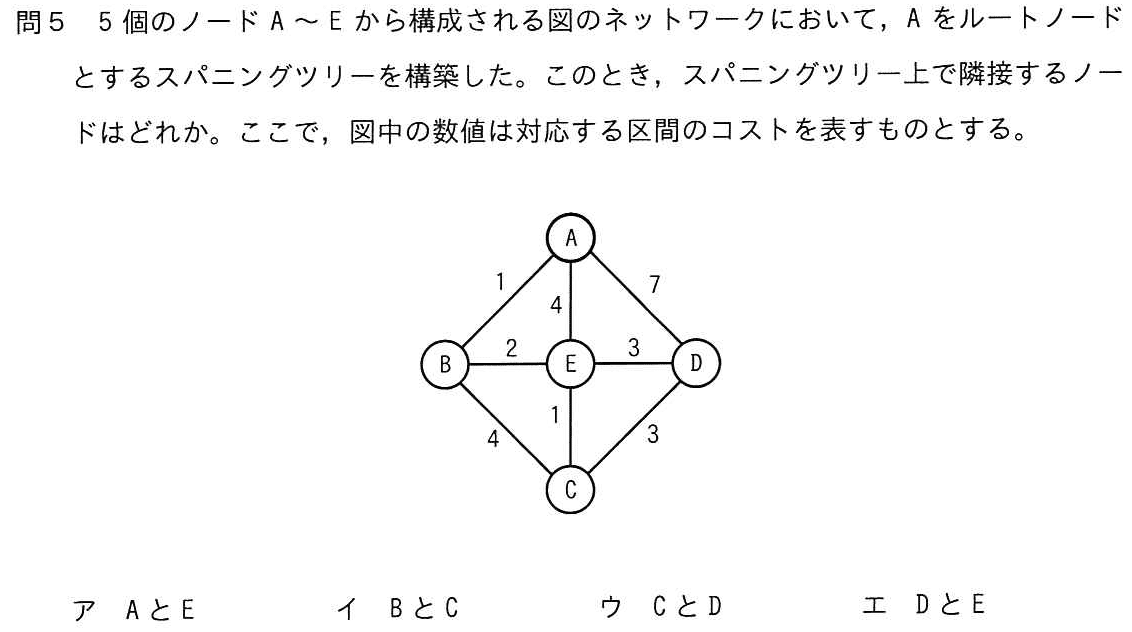
正答はエ(DとE)。
各ノードからAまでコストが最小になるルートを書き出します。
B→A:1
E→B→A:3
D→E→B→A:6
C→E→B→A:4
他の経路ではコストが大きいのを確認しておいてくださいね。
以上より「隣接するノード」は、AとB、BとE、EとD、EとC。選択肢と比較すると、正答はエ(DとE)。
通信負荷に耐える多重度の計算

ネットワークスペシャリスト 平成28年秋午前2問03
ネットワークスペシャリスト 平成24年秋午前2問04
ネットワークスペシャリスト 平成22年秋午前2問02
*作図
Xから出せるのは、11=4+4+3
ABCからDEGへ出せるのは、10=1+2+3+4
XからDEGに伝わるか確認をして、
X→A:4
A→D:1
A→B→D:2
A→B→E:1(残り2)
X→B:4
B→E:2
B→C→F→E:1
※C→F:残り3
※F→E:残り1※X→Bの残り1は通じず。
X→C:3
C→F→E:1
※C→F:残り2
※F→E:残り0C→F→G:2
※C→F:残り0
※F→G:残り1
よって合計10 = 4+3+3
次にYへの到達を考えます。
D→Y:3
A→D:1→Y:1
A→B→D:2→Y:2
※D→Y残り0
E→Y:3、E→G→Y:2
A→B→E→:1→Y:1
B→E:2→Y:2
※E→Y残り0
B→C→F→E:1→G→Y:1
C→F→E:1→G→Y:1
※G→Y残り4
G→Y:2
C→F→G:2→Y:2
※G→Y残り2
よって合計10 = 3+ (3+2) +2。正答はウ(10)。
他の経路パターンも気になると思いますが、XからABC、ABCからEDGへ、最大数接続しているので、問題ありません。もし最大数接続してなかったら、別パターンも考える必要があったかもです。
ルーティング(選択)の計算問題
ネットワークは道路と同じで、ゴールまで色んな経路で行けます。
通信でも、車のナビと同じで、距離や渋滞を考えてルート選択をします。ルーティングプロトコルは種類がありましたね。>ルーティングプロトコルのNote(準備中*)
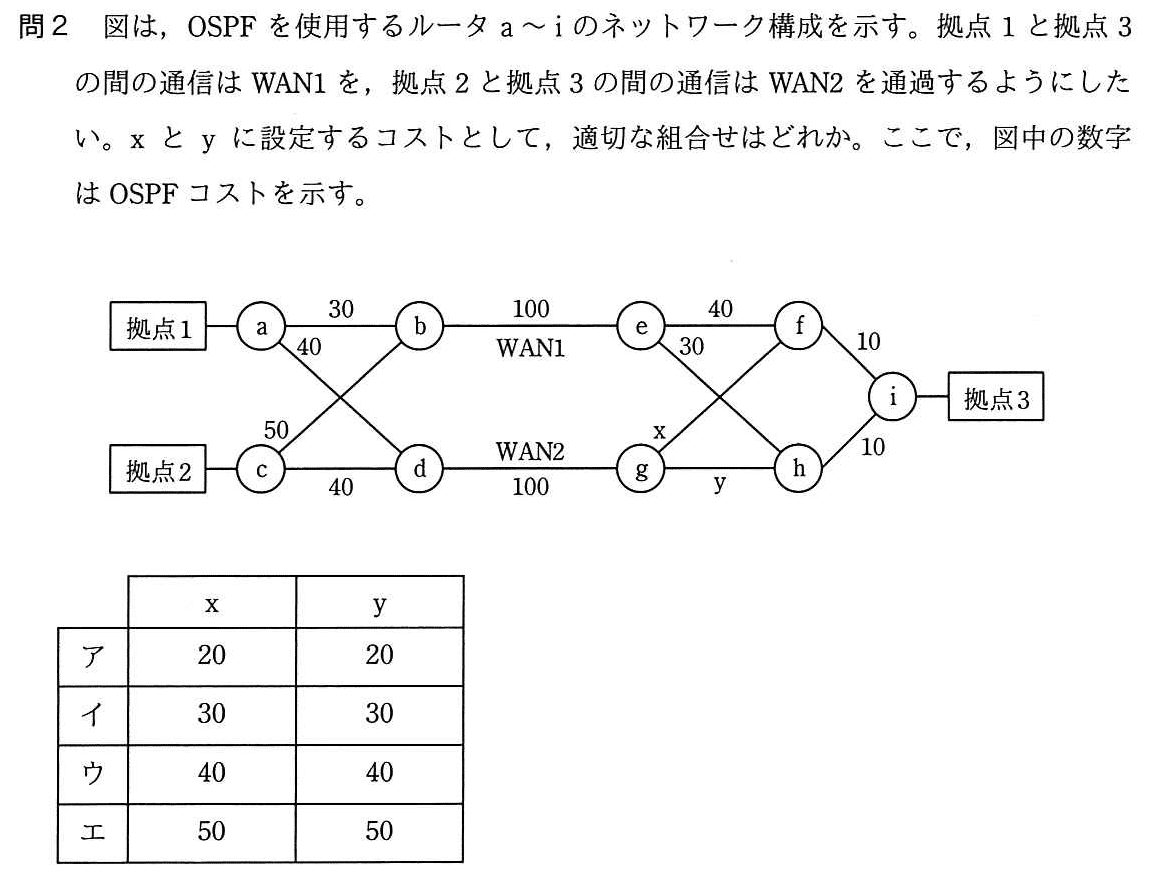
ネットワークスペシャリスト平成28年秋午前2問04
ネットワークスペシャリスト 平成25年秋午前2問04
ネットワークスペシャリスト 平成23年秋午前2問05
ネットワークスペシャリスト 平成21年秋午前2問04
正答はイ。
「拠点1→WAN1→拠点3」のコストが「拠点1→WAN2→拠点3」のコストより小さければOK。また「拠点2→WAN2→拠点3」のコストが「拠点2→WAN1→拠点3」のコストより小さければOK。
コストを計算します。
拠点1→WAN1→拠点3:30+100+30+10=170
※WAN1→e→h→iが最小拠点1→WAN2→拠点3:
40+100+x+10 = 150+x
40+100+y+10 = 150+y
拠点2→WAN2→拠点3:50+100+30+10=190
拠点2→WAN1→拠点3:
40+100+x+10 = 150+x
40+100+y+10 = 150+y
以上より、
拠点1について、170 < 150+x ①
拠点1について、170 < 150+y ②
拠点2について、190 < 150+x ③
拠点2について、190 < 150+y ④
選択肢ア(x=20, y=20)では、①や②を満たせません。
選択肢イ(x=30, y=30)では、①~④を満たします。170<180<190。
選択肢ウ(x=40, y=40)では、③や④を満たせません。
選択肢エ(x=50, y=50)でも、③や④を満たせません。
したがって正答はイ。
まとめ
お疲れ様でした!
今回は計算問題だったので、設問文を読んでその場で考えれば正解できる系でした。各技術の知識はそんなに影響なかったかなと。
各技術の知識を補強しておくと良いかなと、以下に挙げておきますね。
>STPのNote(準備中*)
>多重度のNote(リンクアグリかな(準備中*)
>ルーティングプロトコルのNote(準備中*)
次は>通信プロトコルのNote(準備中*) でお会いしましょう。でわでわ。
\私の3ヶ月の学習記録/
いいなと思ったら応援しよう!

