やっぱりスゴい「すごいぞ折り紙」幾何学をあそびながら学べちゃう。なんとX'masの飾りまで！？

では問題です。

正八面体１つと、正八面体と一辺の長さが同じ正四面体４つの体積では、どちらが大きいか？ または等しいか？ （「すごいぞ折り紙 入門編」 著者 阿部 恒 発行所 日本評論社 抜粋）

算数・数学は、計算ばかりではありません。図形の問題もありますね。上記の問題を簡単に解く方法が、なんと折り紙です。

では解答です。

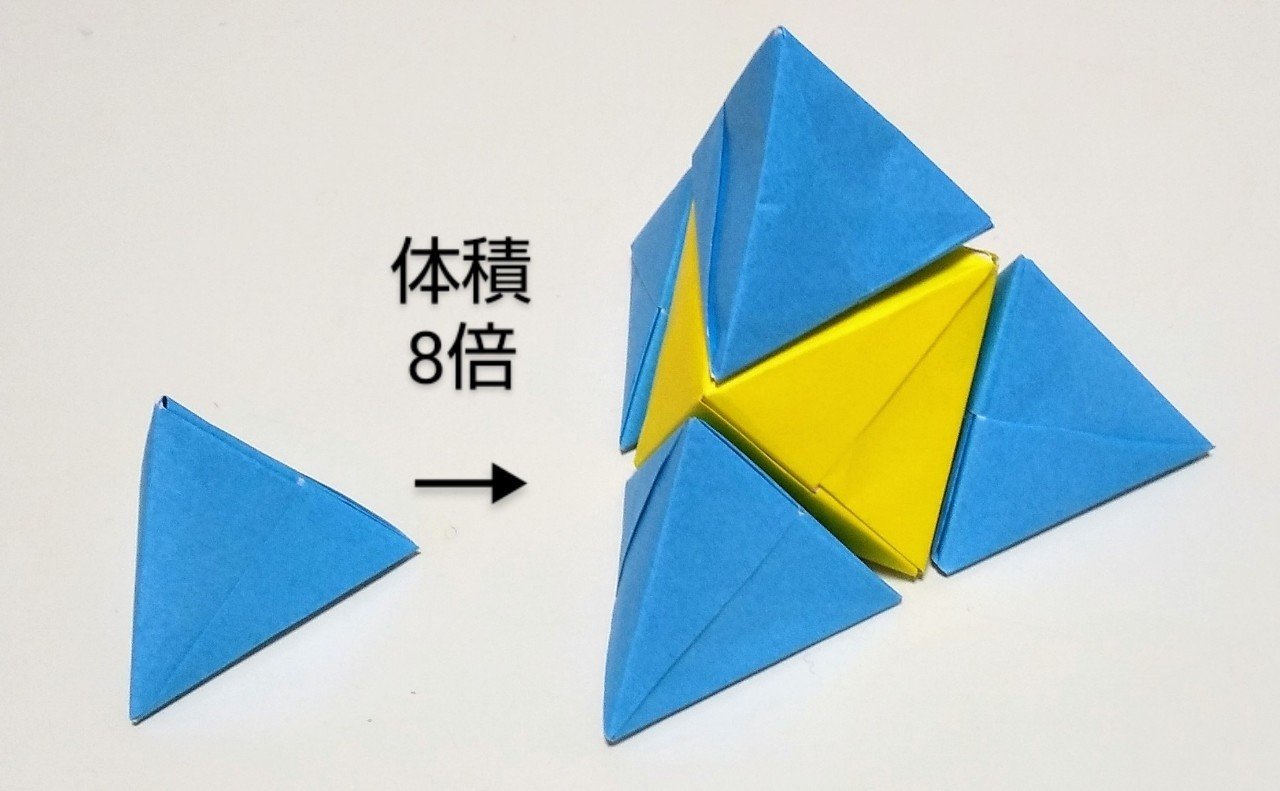
正八面体１つと正四面体４つを下記の写真（右）のように組むと、一辺が２倍の正四面体ができます。

一辺が２倍なので、体積は、小さい１つの正四面体の体積の「８倍」になります。
（２の３乗）

よって、正八面体１つと、正八面体と一辺の長さがが同じ正四面体４つの体積は等しい。
という答えがでました。

こちらの本では、ユークリッド幾何学についても折り紙の技法で解いています。私には難しすぎるのですが、折り紙ならば…。

また、その他にも様々な多面体が紹介されています。

クリスマスの飾りにもなりそうな、コンペイトウを作ってみました。とても簡単でした。

お子さんと、または私のように一人で、
折り紙を楽しんでみてはいかがでしょう。

または、受験勉強の息抜きにでも。

☆正八面体にピッタリかぶさるコンペイトウ
コンペイトウユニット12枚で作成。
（正八面体のユニットと同じ）

詳しくは「すごいぞ折り紙 入門編」ご参照ください。

☆☆☆☆☆
すごいぞ折り紙 入門編
折り紙の発想で幾何を楽しむ

著者 阿部 恒
発行者 黒田 敏正
発行所 株式会社 日本評論社