３Ｄ立体ボードゲームを使って「立方最密充填」を学ぶ（３）

いよいよ最後に、３Ｄ空間におけるサイコロの配置状態をお見せしましょう。今回の話は、最高にキモチワルイですよ。
（不快ではきそう・・というのではなくって、今まで自分が大事にしてきた常識と、これから示される図とが完全に乖離している、というキミノワルサです。）

まずは、化学の教科書とかで、面心立方格子ってのはこんな形状だ、なんて説明されつつ、よく載っている図をご覧ください。

面心立方格子（６個の面の中心に、原子（マル）がある）

図にはしっかりと「立方体」が見えますよね？
今、注目している「この立方体」の、６つの面の中心に、原子（つまり、図としてはマル）を配置するわけです。

ニンゲンのアタマというのは本当に不便なものでして、
「どうして、立方体の中心にマルを置かないんだ？こんな風に、まわりにばっかりマルを置いちまってよォ、これじゃあ真ん中にゃ、どでかいスキマが残ってるぜ！こんな置き方するのは、ドアホウってぇやつだい。ベラボウめえ。」

学生の頃の私自身も、何度も何度も、ここに書いた「錯覚」に苦しめられました。なかなか、そういう「直感」から抜け出せないのですよ。

でも実際には、この図に示す「立方体」の中心付近には、すき間は全くないのです。下の図を見てください。

補助線を引くと、きれいな正三角形が見えるようになる

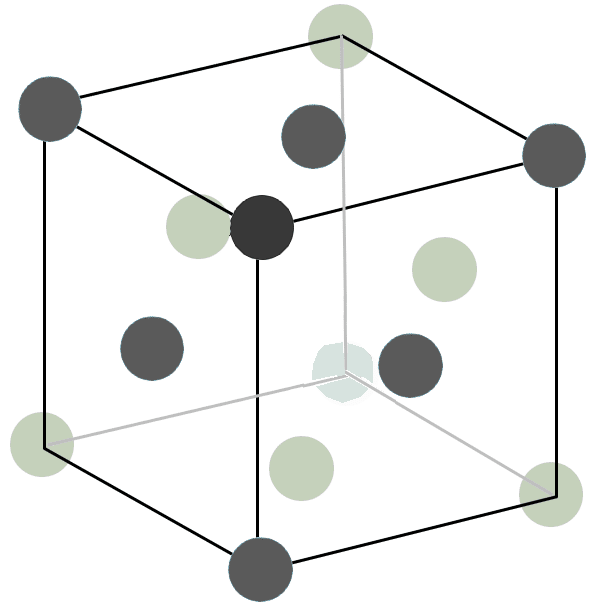
今までずっと説明してきたのと同じ色に、「原子のマル」を着色してあります。
まず最初に「６個の緑の原子（マル）」に注目してください。緑の原子のマルが作る△の中心に、青のマルが乗っかっています。緑の▽の中心には、青のマルは乗っていません。
そして、青のマルが作る△の中心に、赤のマルが乗っているのです。青の▽の中心には、赤のマルは乗っていません。
おまけに、赤のマルとピンクのマルとは、ピッタリ重なって見えるような空間的位置関係にあります。

これらの、緑（６個）→青（３個）→赤（１個）の積み上がり方の位置関係は、Das Spielのサイコロの積み方と完全一致していますよね？
ということはつまり、今見ていた立方体（面心立方格子図）の中心部分付近には、まったく空きはなかったのです。原子（マル）がキチキチに詰まっているのですよ。

Das Spielでサイコロが積まれていく様子

これって、やはりどうしても、直感的には信じにくい（理解しにくい）ことですよね！

ここで、さらに皆さんに追い打ちをかけます。
今まで論じてきた「面心立方格子の図」、これと、Das Spielのサイコロの積み上がり方とは、どっちも「面心立方格子」だよ！
ということで、３Ｄ空間的には、まったく「おんなじ方式」でぎゅうぎゅうに積まれているんだよ。
ここまでは、誰でも簡単に理解できると思います。でも！

下に示したのは、結局のところ、お互いにどういう空間的な配置関係なの？という図です。ともかく、図を見てください。

この図に示すサイコロの「空間的位置」は、赤１マル・青３マルの「空間的位置関係」に一致

あーー。そうなんだーー。と言う風に、ちょっとヤサグレてしまいませんか？こんなモノを見せられたら。

言われてみればそうかもしれない、くらいには納得できるのですが、自分の直感がどこまでも「こんな図は嘘だっ！」って叫び続けているのですよ。いまだに。
ニンゲンのココロというものは、本当に不便なものです。自分で絵を描いているのに、直感のほうが、なかなか言う事をきいてくれません。

追伸：
理系の高校生の皆さん！一番最後に書いたサイコロの話は無視して、もういちど純粋に「面心立方格子」の図の説明のところ「だけ」を読みなおしてみてもらえませんか？
結晶とか、最密充填とかが、ものすごく理解が深まる、良い図を作れたと思うんです。ぜひ勉強にご活用ください。