
【視覚化】ベクトルの内積
統計学基礎を一般の人に教えるにあたり、どうしても高校程度の数学が必要になるのですが、数式を見るだけでケロケロとなる人の気持ちも分からんでもない。
なんとかならないものか。
統計学の視覚化には、ベクトルを含む線形代数が最適。よし、この際、線形代数の基本の視覚化に挑戦し、数学的にも正しく、ごまかさず、かつ難しくないように工夫してみようと思ったのが地獄の始まりでした。
ネットを調べてみても、「一方のベクトルから一方のベクトルへの正射影」みたいな普通の説明はいくらでもあるのに、「成分同士の掛け算の和」がそれと一致することは、数式以外での証明は見当たりません。そこよ、そこ。そこが大事。図形操作だけでできればいいのになあ。
そこで、ああでもないこうでもないとこねくり回した結果、ついには図形操作だけで証明できる方法を編み出し、自分は天才なのではないかと寝ぼけながら寝落ちした夏の深夜3時。
内積全般と普通の説明

内積は普通こう書かれます。
$${\bold A \cdot \bold B =|\bold A ||\bold B|\cos{\theta}=a_1 b_1 + a_2 b_2}$$
以下、毎度$${|\bold A|, |\bold B|}$$と書くのはめんどくさいので、ただの$${a,b}$$と表記します。ちなみに、三平方の定理により、$${a^2 = a_1^2 + a_2^2, b^2 = b_1^2 + b_2^2}$$です。
このうち、$${b\cos{\theta}}$$の部分は、「ベクトル$${\bold B}$$のベクトル$${\bold A}$$への正射影」といい、要するに$${\bold{B}}$$からベクトル$${\bold A}$$の真上からまっすぐ光を当てたときの影の長さです。
これと、$${\bold A}$$の長さ$${a}$$の長さをかけたもの、という説明が普通の説明ですが、確かにその通りではあるけどこれでは何のことかもう一つ分からないし、これが成分の和とどう結びつくかは見当もつきません。
図形操作による内積の証明の流れ
二つのベクトル$${\bold{A,B}}$$を用意し、90度回転させ$${\bold{A',B'}}$$とする。
内積が$${\bold{A,B'}}$$が作る平行四辺形の面積($${|a||b|\cos{\theta}}$$)となることを示す。
$${x}$$成分同士の積($${a_1 b_1}$$)を面積とする平行四辺形を等積変形し、上の平行四辺形にぶちこむ。$${y}$$成分同士も同様。
$${x}$$成分平行四辺形と$${y}$$成分平行四辺形の重なり部分と空白部分が同じ面積であることを証明し、めでたく$${|a||b|\cos{\theta}=a_1 b_1+a_2 b_2}$$でQED。
それでは、行ってみよう。
内積は平行四辺形の面積
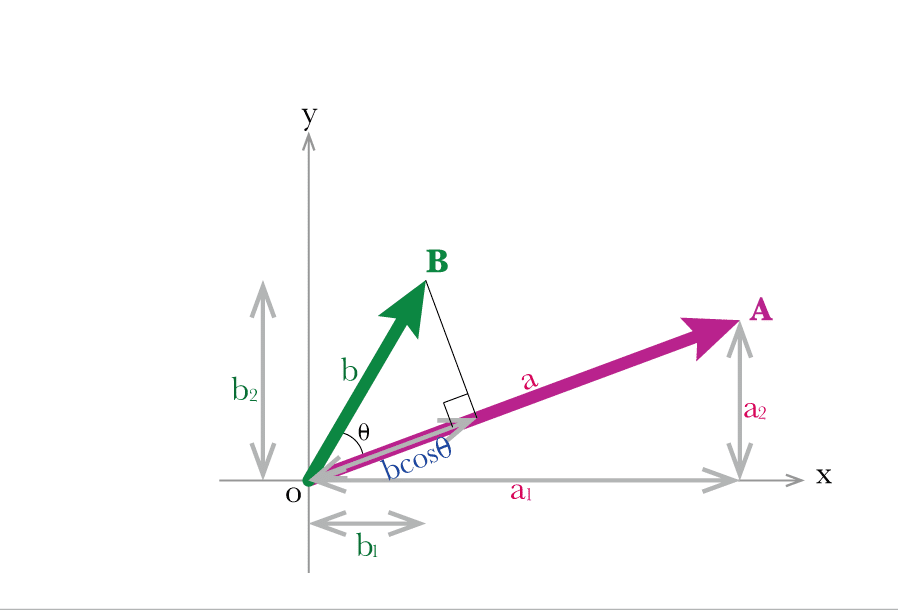
先程と同じ図です。$${ab\cos{\theta}}$$を何とか面積にできないかと考えました。同じ方向だとどう頑張っても面積にはならないので、ベクトルをどちらも90度回したものを用意してみます。

これで面積を作ることができます。この図で$${ab\cos{\theta}}$$は、底辺$${a}$$、高さ$${b\cos{\theta}}$$の平行四辺形の面積(黄色の部分)になりますね。

成分同士の掛け算も平行四辺形の面積
次に、$${x}$$成分同士の掛け算。これも90度回転したおかげで平行四辺形になります。高さ$${a_1}$$、底辺$${b_1}$$、面積$${a_1 b_1}$$ですね。

これをピンクの領域に押し込めたい。よく見ると、横方向に沿って等積変形ができそうです。

おお納まった。いい感じである。次に$${y}$$成分同士もやってみよう。

底辺$${a_2}$$、高さ$${b_2}$$、面積$${a_2 b_2}$$の平行四辺形である。これもピンクの領域に押し込んでみよう。やはり等積変形ができそうだ。

納まった。さっきの$${a_1 b_1}$$と合わせて内積になるはず。重ねてみよう。

うーん、$${S}$$の部分が重なって二重計上になっている。一方、$${S'}$$の部分は空白のまま。
ということは、面積$${ S = S'}$$なら、最終的に$${ab\cos{\theta}}$$と$${a_1 b_1 + a_2 b_2}$$の面積が一致することになる。
補助線を引いてみよう。

平行線を引いてみた。すると、$${S}$$と$${S'}$$の部分に現れる三角形(青い三角形)は全部合同ではないか!
なぜなら、平行線だらけなので角度も等しく全て相似なのは明らかで、対応する辺同士も同じ平行線の間に納まっているので長さも等しいからです。

あとは、残った二箇所のオレンジの部分(形の違う平行四辺形)の面積が等しければゴール。
これも、全て同じ長さの底辺を持ち(全部合同な三角形の長辺)、平行線に挟まれているから高さも等しいのでやはり面積は等しい。
ということで、$${ S = S'}$$となり、図03の黄色の平行四辺形の面積と無事一致しました。
これで、$${a\cdot b=ab\cos{\theta}=a_1 b_1 + a_2 b_2}$$となり、内積の式の本質である、「2つのベクトルの長さと間の角」と「ベクトルの成分」が結びつくことが図形操作で証明できました。
(間の角が鈍角のときは絵の上下が逆転するだけで、そもそも2つのベクトルの間の角を考えたら必ず鋭角になるから大丈夫でしょう)。
式での証明(念の為)
この証明、普通は式で証明して終わりが多いです。
ベクトル$${\bold{A, B}}$$の先っぽを点$${A,B}$$とし、$${AB}$$間の距離を「座標での距離」と「余弦定理での長さ」の二通りで表し、これらが等しいことから導きます。
$$
\begin{align*}
AB^2&=(a_1-b_1)^2+(a_2-b_2)^2\\
&=(a_1^2+a_2^2)+(b_1^2+b_2^2)-2(a_1 b_1 + a_2 b_2)\\
&=a^2+b^2-2(a_1 b_1 + a_2 b_2)\\
AB^2&=a^2+b^2-2ab\cos{\theta}\\
\end{align*}
$$
$$
\begin{align*}
a^2+b^2-2(a_1 b_1 + a_2 b_2)&=a^2+b^2-2ab\cos{\theta}\\
a_1 b_1 + a_2 b_2&=ab\cos{\theta}
\end{align*}
$$
あっさりしたもんです。
上の式を絵にしたものも思いつきましたが、疲れたのでまたの機会に。
