
算数 | なぜ分数のわり算では逆数をかけるのか?
以前、分数の足し算について記事を書いたことがある。
今回の記事はその続編である。
分数の計算それ自体は出来ても、子どもから「分数のわり算では、なぜ逆数をかけるの?」と聞かれたら、即答できるだろうか?
やり方を覚えていれば、答えを導くことはできるが、「大人の算数」においてはテストはない。今は気楽に「なぜ?」を考えてみませんか?
(1)わり算ってそもそもなーに?
一番最初に「わり算」を学んだときは、おそらくこんなふうに習ったはずだ。
12枚の折り紙があります。4人で同じ枚数に分けたら、1人何枚になりますか?
12枚の折り紙を4人で分けるのだから
12➗4 = 3
(こたえ)1人あたり3枚。
「わる数」よりも「わられる数」が大きくて、どちらも整数のときは比較的イメージしやすい。
⚠️ 「A➗B」で、Aのことを「わられる数」と言い、Bのことを「わる数」と言う。
しかし、例えば「わる数」が小数だったら、どう考えたらよいか?
1➗0.2 = 5 だが、「わる数」が「0.2」だとイメージがしにくい。
だから、少し言い方をかえる。
「1」の中に「0.2」はいくつ入りますか?と。
「0.2」は「1」の中に「5個」入る。
だから、1➗0.2 = 5 となる。
もう一度整理して言うと、
「A➗B」の意味は、
「『B』は『A』の中に何個入りますか?」ということでしたね😄。
(2) 「1➗3」の意味を考えてみよう!
12➗4 の計算ならば、次のようなイメージである。

全体が「12」ある中に、「4」は「3」つ含まれている。
では、「1➗3」はどうだろう?
全体が「1」ある中に「3」はいくつ含まれているか?
たとえば、タイルがあるとする。
1枚のタイルの中に、その3倍の大きさの面積を持つタイルをのせようとしたら、元のタイルの2枚分がはみ出してしまう。

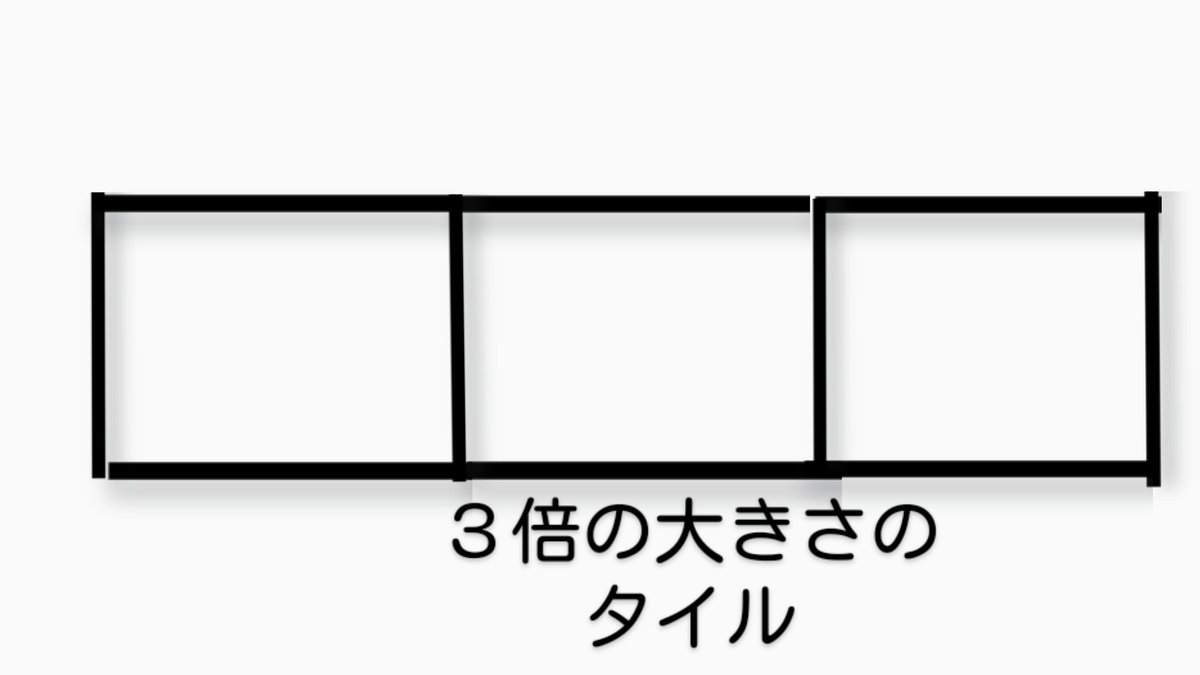
「A ➗ B」 の意味は、「B」は「A」の中にいくつ入るかということだった。
「3倍の面積を持つタイル」が、元のタイルと重なる部分は、1/3 (3分の1)。
だから、1➗3=1/3 である。
(3) 1➗1/3 だったら?
くどいかも知れないが、もう一度言うと、「A➗B」の意味は
「BはAの中にいくつ入りますか?」だった。
1 ➗1/3ならば、
3分の1は、1の中にいくつ入りますか?
(こたえ) 3つ
ということは
1➗1/3 = 3
結局、1➗1/3 = 1✖️3。
こじつけたような説明だが、一応、分数のわり算では、「逆数」をかけたようなこたえになりそうだ(という雰囲気😄)。
(4) 6➗3 も 12➗6 も同じ。
6➗3 は、「3は6の中にいくつ入りますか?」の意味。


「2」つ入る。
12➗6 は、「6は12の中にいくつ入りますか?」の意味。
今、上(↑)で使った図を再利用します😄

「一目盛り『2』」と読めば、
結果は同じ💝
「A➗B」という計算の答えは、
「2A➗2B」としても成り立ちそう。
実際に、「わられる数」と「わる数」を、それぞれ「2倍」しても「3倍」しても同じ結果になる。
というのは「2倍」「3倍」というのは、「一目盛り」を「2」にするか、「3」にするか、というだけのことだから。
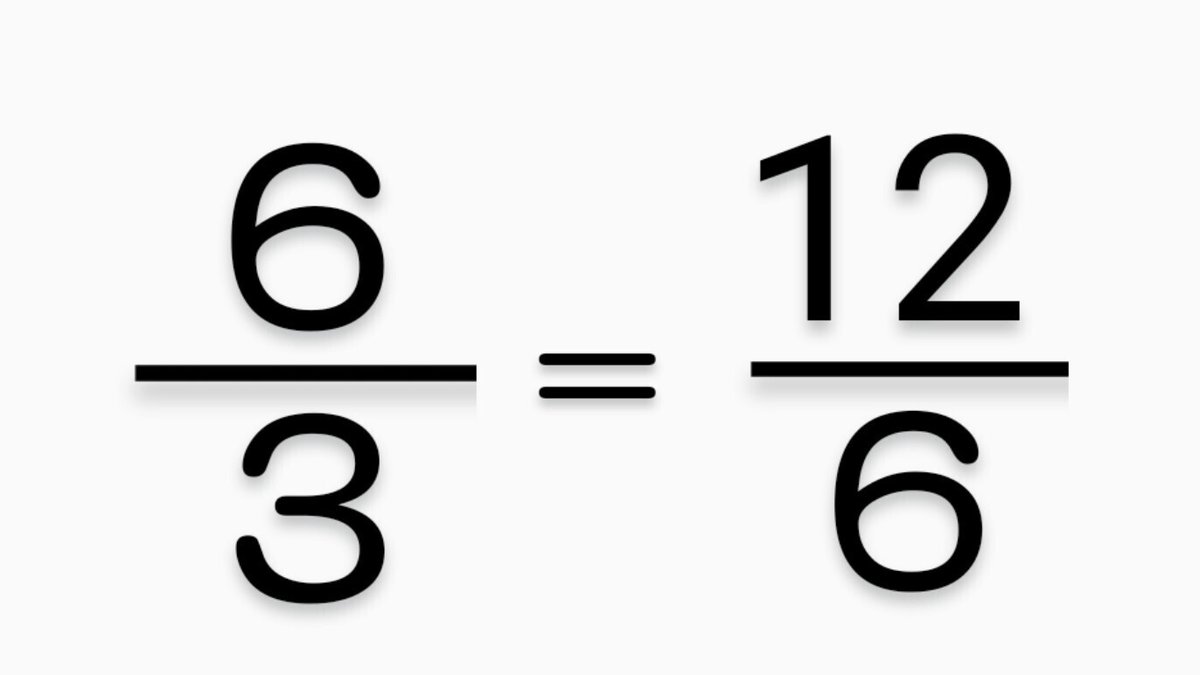
同じ数をかければ
結果は同じ。

(5) 2➗2/5 は?
数直線で「2」を表すと(↓)、
こんな感じ。
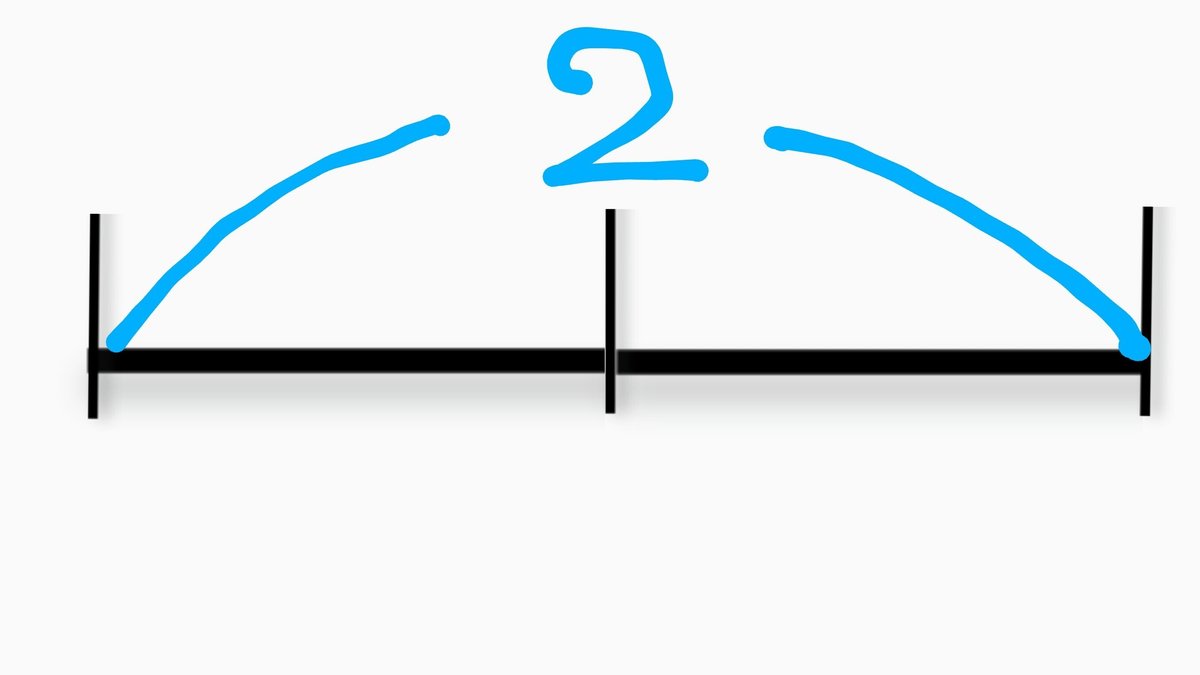
5分の1( = 0.2 )の目盛りにすると、

この中に2/5 はいくつ入るだろうか?
「5分の2」は「5分の1」の「2個分」である。
2の中に「5分の1」は「10個」含まれているから、
10 ➗ 2= 5
つまり
2➗(2/5)=5
こたえは「5」になる。
(4)の最後に書いたことを、分数の場合にも成り立つと考えれば、次のような計算になる。

結局、答えは「5」になる。
文字のみで書けば
A ➗ B/C の計算は

分数のわり算では、逆数のかけ算をすればよいことが分かる。
まとめ
今回記事を書いてみて、分数のわり算で「逆数」をかけることを説明することは難しいと思った。
「比の値」で説明するのもよいと思う。
算数というか数学は、個別具体的に計算することやグダグダと説明されるよりも先に「飛躍」することがある。
「逆数をかける」ことも「なぜ?」と考えるよりも先に「暗記」した。
逆数をかけることで、それまでに学んだ知識と矛盾することがなければ「受け入れる」。
「暗記すればいいんだよ」という言葉はスキではないが、1個1個「何で?」と思っていたら前に進めない。どこかで理屈抜きで覚えてしまったほうがいい。テスト対策としては。。。
学校を卒業したら、「当たり前」を疑ってみる。学生時代に「なんで?」と思ったことが知らぬ間に理解できるようになっていることもあるかも😄。
いいなと思ったら応援しよう!

