
悪魔の数学😈円周率は2である
悪魔😈からのメッセージ
円周率が2ですって(*_*)。
円周率は3.141592…とずっとつづく無理数だったはずではないか!!
大幅に譲歩したって「3」。2であるはずがないではないか!!
ご批判は甘んじて受けましょう。でも😈私は、円周率が2であるという真理にたどり着いてしまったのです!!
これから「円周率は2である」ということを明確に証明してみせましょう😈
😈そんなに難しくないよ。中学1年生レベルの知識があれば十分だから、ついて来てね😈
😈悪魔の証明
「円周率は2である」
証明
つぎのような半径1cmの半円(↓)がある。

半径 r cmの円の周の長さ l は
l = 2πr ・・・① だから、
半径 1cmの半円の弧の長さは、①の公式に r = 1を代入して、2で割ればよいから、
2π × 1 ÷ 2 = π
よって、
半径1cmの半円の弧の長さは
π cmである。

半径1cmの
半円の弧の長さは
π cm
(青い部分)
😈ここまでは問題ないかな?
人間でも、中学1年生くらいの学力があれば、きっと分かるだろ?たぶん。
じゃあ、話をつづけよう✨

😈今度は、今と同じ半径1cmの半円の中に上のような半円(半径1/2)を2コかいてみる。
そうすると、(計算は省略するが)「赤い部分」の長さは、
π cmとなる。
つまり、先ほどの図1の「青い部分」の長さとまったく同じである。

(↓)の赤い部分も
いずれもπ cm

😈今度は半径1cmの半円に3つ半円をかきこんでみる(↓)。

π cm
計算は面倒だから省略するが、
「緑色の部分」の長さは
やはり π cmとなる。
つまり、半円の直径を4等分して、半円を4つかいても、周の長さの和は、「青い部分」(元の半径1cmの半円の弧の部分)と同じになることが予想される。
実際に計算してみれば、5等分でも6等分でも、「周の長さの和」はいずれも「π」となり、「青い部分」と同じであることがわかる。
😈ここまでは大丈夫かな?
ところで、今のような感じで、無限に等分して半円をかきこんで行けば、やがて半径1cmの半円の「直径」に限りなく近づいていく。
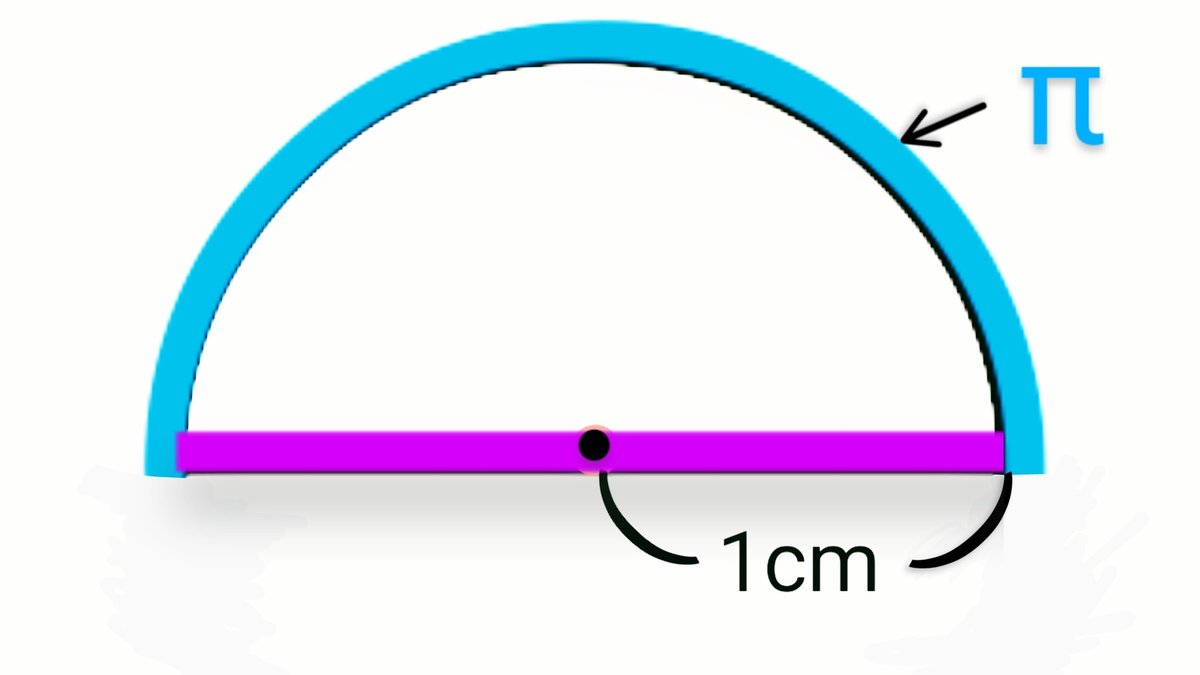
図3の「紫色の部分」は、無数に半円を書き込んだものである。
つまり、その周の長さの和は
π cmである。
図3の「青い部分」も「紫色の部分」も、いずれも π であることがわかった。
😈ここで図をよ~く見てほしい。
どう見ても「紫色の部分」は半径1cmの半円の直径ではないか!!
つまり、「π=2」ということである。
Q.E.D.
😈どうだい?
円周率 π は、2だということがよく分かっただろう?
納得がいかないって!!
不服があるなら反論してみな!
できないだろう😈
では、サラバ😈😈
いいなと思ったら応援しよう!

