2021年 共通テスト数学IA　感想戦

先日、共通テストが実施された。
数学科講師として数学IA・数学IIBを解いた訳だが、せっかくなので思ったことを書き残して置こうと思う。ここではまずIAの感想戦を行う。あとは、自分で解いた時にかかった時間もメモとして残しておく。かかった時間でおよその難易度の目安になるかもしれない。

IA第1問[1]　未知数cを含む二次方程式（4分13秒）

具体的なcの値に応じて二次方程式を都度解いていく前半と、解が有理数になるようなcの個数を数える後半との構成。前半のただの計算はともかく、後半は太郎花子の会話から「根号の中が平方数になるようなcを数える」ことに気付けるかがポイントだった。また、整数部分を求める問題も出題されたが、√65の値を8と9で挟めれば問題なかっただろう。
難易度としては前半は易しめ、後半は平方数をcごとに全部検証する必要があるがそれだけこなせばよく、普通といったところか。

IA第1問[2]　三角比と図形計量（8分7秒）

最序盤は三角形の要素を求める問題で、これは公式を正しく使えば良いだけ。この段階で、図中に現れる三角形の面積はどれも等しいことに気がつく。また、各辺を1辺に持つ正方形の面積の関係式から鋭角・鈍角条件を余弦定理と結びつけて考えたり(公式として処理しても良い)、角度の大小に応じた外接円の半径の大小比較をしたりと、何をしなければいけないかがぱっと見でわかりづらいものが後半ほど多かった。

特に後半の外接円の考察は曲者だった。前半の面積の考察部分・補角の公式から、鋭角な角と対辺の組み合わせに注目すれば外接円の半径が小さくて済むことに気づく必要がある。鋭角鈍角に応じた大小比較の誘導があるので、これにしっかり乗れたかで勝敗が決まる問題であった。

前半部分は易しく、後半にいくにつれ難易度が上がる。最後の外接円の半径の大小比較はやや難しめである。特に、数値による比較ではなく、大小の性質を利用しての比較だから、求めた値に対して検算をして自信を持つこともできないのが少し辛かった。

IA第2問[1]　二次関数の最大最小(ピッチ・ストライド)（5分24秒）

短距離走を数理モデルとして捉えて考える問題であった。

ピッチ・ストライドがどのように定義されるのかを正しく把握できれば、名前はただの飾りであり、与えられた文字に従って立式すれば典型的な二次関数の最大最小問題に帰着される。ただ、二次関数のパターン練習ばかりしてるとこの手の「与えられた定義にしたがって考える」類の問題は解けない人が多そう。数学の基本は「定義に還る」であることを考えさせられる問題であった。

モデルとして状況を把握できれば、すべきことは易しい。状況把握と合わせて普通の難易度といったところか。

ちなみに、途中で8.8を分数で答えさせるくせに、そのあとの答えは小数で表記されたり、小数第２位はことごとく０だったりと、出題サイドの微妙な点が目立つ。

IA第2問[2]　データの分析（9分23秒）

産業ごとの就業者数割合を題材に、箱ひげ図・ヒストグラム・散布図と相関を「読み取る」問題だけ出題された。数値の計算が一つもないのが目新しい。その分、1つ1つを丁寧に読み取らなきゃいけないので、時間がかかる。

個人的には読み取り問題が多すぎだと思う。読み取りは確かに数学活用と言えるかもしれないが、やりすぎると一般教養問題みたいになってしまうし、一回も計算をしないデータの分析となってしまっていてバランスが悪い。

時間を大幅に食われる構成なので、飛ばしてあとで戻ってきた人もいるかもしれないが、難易度自体は普通。どれだけ時間を確保できたかが鍵である。

IA第3問　確率(反復試行・条件付き確率)（9分8秒）

くじの入った箱を選び、反復試行としてあたりくじを3回中1回引ける確率を考える問題。当たりくじを引ける確率が違う箱が最終的に4箱現れ、すべて確率を計算した上で大小を比較する必要がある

序盤は典型的な計算問題なのだが、その計算結果も、面倒な分数(32/59など)になる。人生をかけた試験で、この分数を目の前にしたら焦るだろうなぁ。
後半の条件付き確率は、定義通りの確率の商ではなく、確率の比率を元に求める問題で、誘導はあるが、計算量が多く大変だった。最後の問題に至っては4つの分数の比較なのだが、分母の通分がしにくい4つの分母になるため、小数表記にしておよそどれくらいの値かを検証した方が早かった。

確率としては同じことを延々と違う条件でやらされるだけ、分数の比較をさせられるだけなので、作業量が多い。その意味で全体的にはやや難しいかもしれないが、1つ1つの問題としての難易度はやや易しめ。この手の「作業量の多さで難易度をあげる」構成はセンターから変わらず。「思考力」を問う形式とは到底言えないと思う。

IA第4問　整数(不定方程式・15を法とした同値類)（10分29秒）

一周を15個の頂点で分割し、各方向に進める頂点数が決まっている問題。方向毎の進行回数を未知数とした不定方程式を解いたり、1周進むと元に戻ることを用いて最小回数を考える後半の問題からなる。最後の問題に至っては5つの頂点の最小移動回数を比較する必要がある。

不定方程式の典型的な解き方を理解できていれば序盤は容易なのだが、途中から(一般化すると)5x - 3y = 15z + kの整数解のうちx+yが最小のものを考えることになる。両辺共に15を法とした同値類に属すことを利用すればxを3減らし、yを5減らすことができるとわかる。具体的な解を手始めに発見し、、xとyの値をそれぞれどこまで減らせるかを考えるのが良いだろう。あるいは、移動回数ごとの樹形図を書き、到達できる点を移動回数が少ない順に網羅していくという力技も考えられるが、いずれにせよ大変面倒な問題であった。

最後の問題の難易度は難しく、それ以外は普通。最初の不定方程式のところだけ易しいぐらい。

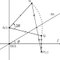
IA第5問　図形(角の二等分線・法べき・内接円と外接円・同一円周上にある条件)（12分49秒）

3辺の長さが3,4,5の直角三角形から、角の二等分線、外接円、2辺と外接円に内接する円、中心同士を結ぶ直線と、次々図を書き込んでいくことになる。

指定された条件通りの図を都度かければなんとかなるのだが、余白量との兼ね合いが一番のネックだったかと思う。各値を求めるためにすべきことはわかりやすい（誘導が付いているところ多数。「方べきの定理により〜」とか）のだが、図がわかりにくいせいで手間がかかる。常日頃の図形訓練が物を言う。

最後は円に内接する条件を満たすかどうか正誤判定であった。ここまでの流れで円の半径と接線、半円の円周角など、90度に散々注目しているので、対角の和が180度になるか判定すれば良いだけであり、そこまで難しくはない。全体的な難易度も普通といったところか。

個人的失敗として、指定された通りの図を書くことに一度失敗した。そのため、時間を3分くらいロスしている。

IA全体としての感想

試行調査のときにあった太郎と花子の会話はかなり控えめになり、試行調査とセンター試験の中間ぐらいの出題構成で落ち着いたといった印象を受けた。ただし、一般的な現象を数理的に考察する問題は多くなったため、パターンマッチなどの勉強しかしてこなかった受験生は悪戦苦闘を強いられただろう。平均点予想は難しいが、例年よりも少し低いあたりで着地すると予想しているが、果たしてどうなることか。

なお、共通テストに向けて対策をすることばかりに気をとられると、数学的な思考力は多分伸びなくなる。日頃の学習は二次・私大に向けてちゃんと対策をし、直前期に共通テストの形式に慣れる訓練をするぐらいがちょうど良い。

ここでいう二次私大に向けての対策とは、「なぜそうなるのか」や「それは何か」といった当たり前の疑問をないがしろにせず、しっかりと自分なりに説明できるようにしようという姿勢で学習することにある。意味もわからず問題を解いているようではダメだということである。

さらに加えていうならば、計算力は必須と言っていい。「わかる」だけではなく「できる」まで意識して日頃から手を動かすことを心がけなくてはならない。

今年は共通テスト1年目でどこもかしこも手探りな受験であった。来年以降の共通テストに向けて、来年度の受験生やそれ以降の受験生はどのように数学と向き合うか、今一度考えるチャンスにしてほしい。