
生産者理論(7):利潤と会計利益
ここまで議論してきた生産関数や生産費用の概念を用いて、企業の利潤最大化行動を分析する。ミクロ経済学上の「利潤」と会計上の「利益」の橋渡し役となるLegendre変換を導入することで、価格や利潤などの会計情報がミクロ経済学上も重要な情報を要約していることが示唆される。連載はこちら。
利潤と会計利益
等利潤曲線と生産関数
生産者理論(3)で導入した利潤最大化問題では、生産ベクトル$${y=(y_1, \cdots, y_N)\in \R^N}$$を純産出量の組として、以下のように定式化した。
利潤最大化問題:$${\displaystyle\max_{y \in Y} p\cdot y}$$
$${y}$$の各要素が投入要素と産出要素に分離できるとき、利潤$${\pi}$$を総収入(全ての生産物の価格と産出量の積の総和)と総生産費用の差と定義し、$${\pi}$$を最大化する産出ベクトル$${y}$$と可変生産要素の投入ベクトル$${x_v}$$を選択する問題として、次のように定式化される。
短期の利潤最大化問題:
$${\pi(p, w, \bar x_f)\equiv \displaystyle\max_{x_v, y}\displaystyle\sum_{i=1}^mp_iy_i-\Bigg\{\displaystyle\sum_{i=1}^kw_ix_i+\displaystyle\sum_{i=k+1}^Nw_i\bar x_i\Bigg\} \\ \text{s.t.} F(x_v, y, \bar x_f)=0}$$
全ての生産要素の投入量が可変となる長期では、以下のように表される。
長期における利潤最大化問題:
$${\pi(p, w)\equiv \displaystyle\max_{x, y}\displaystyle\sum_{i=1}^mp_iy_i-\displaystyle\sum_{i=1}^Nw_ix_i \\ \text{s.t.} F(x, y)=0}$$
生産要素、生産物とも1種類かつ生産関数$${f(x)}$$が凹関数の場合を考える。
$${\pi = py - wx =pf(x)-wx}$$
において$${x=x^*}$$の時$${\pi}$$が最大化されるための条件は、以下で与えられる。
$${\begin{cases} \dfrac{\partial \pi}{\partial x}=pf'(x^*)-w=pMP(x^*)-w=0 \\ \\ \dfrac{\partial^2 \pi}{\partial x^2}=pf''(x)≤0 \end{cases}}$$
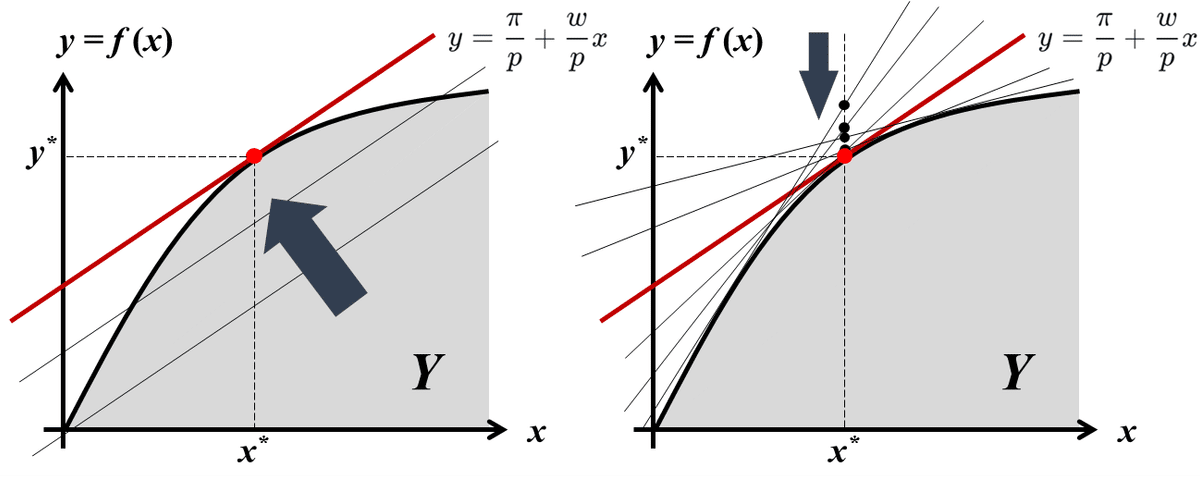
つまり最適な生産計画において、限界生産性$${MP(x^*)}$$は生産要素と投入要素の価格比$${\dfrac{w}{p}}$$に等しい。2階の条件は、生産関数の凹性を仮定しているため満たされる。図形的には価格体系$${(p, w)}$$を所与として、傾き:$${\dfrac{w}{p}}$$、切片:$${\dfrac{\pi}{p}}$$の直線(等利潤曲線)と生産関数との接点が最適な生産計画となる。以下の左図のように、上方に位置する等利潤曲線ほど高い利潤に対応しており、傾き一定のまま切片を生産関数と接するまでシフトさせる。
$${\pi = py - wx \Leftrightarrow y=\dfrac{\pi}{p}+\dfrac{w}{p}x}$$
$${f(x^*)=\dfrac{\pi}{p}+\dfrac{w}{p}x^*, \dfrac{d}{dx}f(x^*)=MP(x^*)=\dfrac{w}{p}}$$
ここで「生産関数は無数の等利潤曲線の下側を接しながら通る」ことを踏まえ、生産関数の任意の点で接する無数の等利潤曲線のうち、$${x=x^*}$$において最も下に位置する等利潤曲線を探索することを考える。上記の最適解$${(x^*, y^*)}$$を所与とした時、価格体系$${(p, w)}$$を変化させた時の等利潤曲線の最小値が、最適解$${(x^*, y^*)}$$における生産関数の値$${f(x^*)}$$に等しい。
$${\displaystyle\min_{\pi, p, w} \bigg\{\dfrac{\pi}{p}+\dfrac{w}{p}x^*\bigg\}=f(x^*)}$$
図形的には以下の右図のように、$${x=x^*}$$で接する等利潤曲線を求める問題に対応する。逆に、企業が利潤最大化行動を常にとっているとの前提の下で、様々な利潤に対応する等利潤曲線を引き、その下側を接しながら通る曲線を求めることで、生産関数を逆算することが可能となる。このプロセスは、数学的にはLegendre変換を用いることで定式化することができる。
補足:Legendre変換
Legendre変換は、ある関数$${g(x)}$$が与えられた時、その関数の微分を独立変数にとる別の関数$${h(a)}$$を構築する操作のことである。
Legendre変換関数
$${g(x)}$$に対して、$${h(a)=\displaystyle\max_x \{ax-g(x)\}}$$で定義される関数$${h(a)}$$を$${g(x)}$$のLegendre変換という
微分を用いたLegendre変換の表現
$${h(a)=ax-g(x)}$$、但し$${x}$$は$${a=g'(x)}$$を満たすもの
例えば$${g(x)=kx^2 (k>0)}$$とすると、$${h(a)}$$は以下のように計算される。
$${h(a)=\displaystyle\max_{x} \bigg\{ ax-kx^2 \bigg\}=\displaystyle\max_{x} \bigg\{ -k\bigg( x-\dfrac{a}{2k}\bigg)^2+\dfrac{a^2}{4k}\bigg\}=\dfrac{a^2}{4k}}$$
一方$${g(x)}$$の接線のうち傾きが$${a}$$であるものの方程式は、接点が$${x=\dfrac{a}{2k}}$$より$${y=ax-\dfrac{a^2}{4k}}$$となる。従って$${g(x)}$$のLegendre変換$${h(a)}$$は、傾き$${p}$$の直線で$${g(x)}$$と交わるものの中で最も下側にあるものの切片(に負号を付したもの)という意味を持つ。幾何学的には、ある関数$${y=g(x)}$$は座標点$${(x, y)}$$の集合と考えられるが、同時に$${g(x)}$$は各点で接する接線によって作られる包絡線と捉えることも可能である。つまりLegendre変換は、座標点$${(x, y)}$$で構成される$${g(x)}$$に対して、接線の傾きと切片の組$${\bigg(a, -\dfrac{a^2}{2k}\bigg)}$$で再構成する変換、と解釈することができる。
また$${g(x)}$$が凸関数の場合、Legendre変換により得られた$${h(a)}$$を関数を再びLegendre変換すると、元の$${g(x)}$$に戻ることが知られている。
今回は生産関数$${f(x)}$$の凹性を仮定しており、負号を付した関数$${-f(x)}$$は凸関数となるため、これを$${g(x)}$$と置く。
$${g(x)=-f(x), a=g'(x)=-\dfrac{w}{p}}$$とすると、
$${h(a)=\displaystyle\max_x \Bigg\{f(x)-\dfrac{w}{p}x\Bigg\}=f(x^*)-\dfrac{w}{p}x^*=\dfrac{\pi}{p}}$$
一方、$${g(x)=\dfrac{\pi}{p}, a=-\dfrac{w}{p}}$$とすると、
$${h(a)=\displaystyle\max_x \Bigg\{-\dfrac{\pi}{p}-\dfrac{w}{p}x\Bigg\}=-\displaystyle\min_x \Bigg\{\dfrac{\pi}{p}+\dfrac{w}{p}x\Bigg\}=-\Bigg(\dfrac{\pi}{p}+\dfrac{w}{p}x^*\Bigg)\\=-f(x^*)}$$
となる。つまり$${g(x)=-f(x)}$$と$${h(a)=\dfrac{\pi}{p}}$$がLegendre変換によって結ばれるため、以下図のように、様々な利潤に対応する等利潤曲線を引き、その包絡線を求めることで生産関数を逆算することが可能となる。

利潤と会計利益
企業が産出物を販売して得た売上を、ミクロ経済学(価格理論)では収入と呼ぶ。またミクロ経済学上の費用は、投入物に係る費用(原材料費など)、労働力への支払額(賃金)、資本への支払額(利子と当期純利益の一部)からなる。
以下の図の総費用と利潤はそれぞれ、ミクロ経済学上の費用と利潤(超過利潤)を示し、ミクロ経済学上の超過利潤は会計上の利益である当期純利益とは一致しない。これは会計上の費用に、経営能力や資本をその産業で使うことの機会費用である正常利潤を加えたものをミクロ経済学上の費用と見なすためである。従って、総収入と総支出の差として定義される利潤は、正常利潤を超える超過利潤を表し、会計上の利益(当期純利益)とは異なり、当期純利益から正常利潤を差し引いたものである。
「総収入」-「総費用」=「(超過)利潤」=「当期純利益」-「正常利潤」

ミクロ経済学上の超過利潤を表す会計上の概念として、残余利益がある。残余利益は資本から生み出されるべき利益(=正常利潤)を上回って稼ぎ出された分の利益として定義される。残余利益の定義については以下を参照。
残余利益の時系列特性は採用されている会計制度により異なるが、資本測定バイアスのない会計(長期的に株主資本簿価が時価と一致すると期待される会計測定。公正価値会計はその一種)では残余利益は超過利潤を表していると考えられる。一方、バイアスのある会計では、会計上の残余利益は必ずしもミクロ経済学上の超過利潤を反映しているとは限らない(例えば研究開発投資の費用処理が強制されていれば、正の残余利益は経済的超過利潤ではない)。
会計情報とミクロ経済学の邂逅
かくして、企業の会計情報や価格情報から等利潤曲線が導出でき、それをLegendre変換することで生産関数を逆算することができる。会計情報は生産関数のLegendre変換であり、会計情報をLegendre変換すると生産関数に戻るため、価格や利潤などの会計情報が、ミクロ経済学上も重要な情報を要約しているとも言える。
Legendre変換を通して、一方ではここまで議論してきた価格理論などのミクロ経済学上の様々な分析手法を生産関数を通じて利用することができ、他方では会計上の残余利益を用いた企業価値評価や経営組織の分析に応用することが可能となる。前者は「価格理論」マガジンにて連載してきた通りだが、後者についても「企業価値評価」マガジンにて連載中のため、両者の理論を橋渡しする概念を今回導入するに至った。
利潤と生産費用
続いて、費用関数を用いて利潤最大化問題を定式化する。短期費用関数を用いた利潤最大化問題の最適解は、固定費用関数が産出量に依存しないため可変費用関数を用いた最適化問題の最適解と一致する。
$${\displaystyle\max_y py-C(y, w_v, w_f, \bar x_f)=\displaystyle\max_y py-C_v(y, w_v,\bar x_f)}$$
最適解において生産物価格$${p}$$(=限界収入)は、内点解である限り常に限界費用$${MC(y^*)}$$と等しい。
$${\dfrac{\partial}{\partial y}C_v (y, w_v, \bar x_f)=MC(y^*)=p}$$
更に、2階条件として最適産出量において以下が成立する。つまり限界費用曲線は右上がりとなる。
$${\dfrac{\partial^2}{\partial y^2}C_v (y, w_v, \bar x_f)=\dfrac{\partial}{\partial y}MC(y^*)>0}$$
これは、生産関数の準凹性を仮定した時、利潤最大化点が以下の2通り考えられるが、最適点において産出量が正ならば、生産は生産関数の収穫逓減部分で行われていることを意味する。なぜなら以下図の左下の接点において、産出量を増加させることで利潤を増加させることが可能となるためである。

ここで、以下の2つの価格概念を定義する。
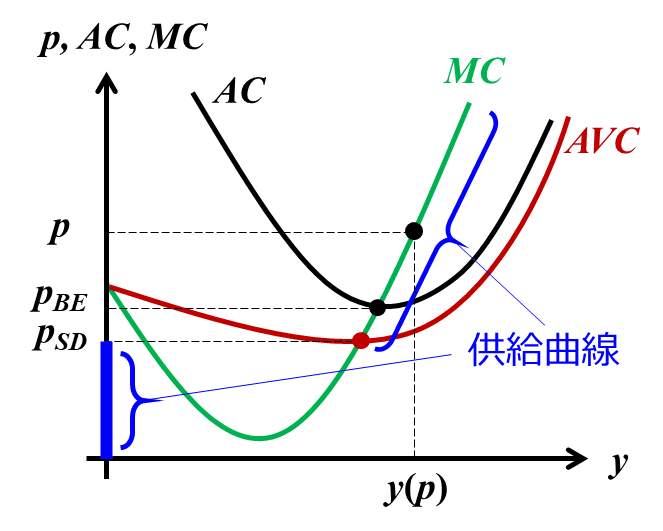
生産中止価格$${p_{SD}}$$:生産物価格$${p}$$が、限界費用曲線$${MC(y)}$$と平均可変費用$${AVC(y)}$$の交点(=$${AVC(y)}$$の最小点)で定義される価格$${p_{SD}(w_v, \bar x_f)}$$を下回れば、いかなる生産量の下でも営業利益は負となり、生産中止$${(y^*=0)}$$が最適となる。この価格は生産中止価格と呼ばれる
損益分岐価格$${p_{BE}}$$:生産物価格$${p}$$が、限界費用曲線$${MC(y)}$$と平均費用$${AC(y)}$$の交点(=$${AC(y)}$$の最小点)で定義される価格$${p_{BE}(w_v, w_f, \bar x_f)}$$より大きい時、最適生産量の下で利潤は正となる。この価格は損益分岐点価格と呼ばれる
$${p_{SD}≤ p≤ p_{BE}}$$の時、営業赤字は不可避だが操業すれば固定生産費用の一部を回収可能となるため、価格が損益分岐価格を下回っていても、生産により赤字を縮小可能であれば最適生産量は正となる
従って、$${y(p)}$$を限界費用が平均可変費用を上回る部分についての限界費用関数$${MC(y)}$$の逆関数とすると、任意の生産価格$${p}$$の下で利潤を最大化する最適産出量$${s(p, w_v, \bar x_f)}$$は次のように表される。
$${s(p, w_v, \bar x_f)=\begin{cases} 0 \text{if} p< p_{SD} \\\{0, y(p)\} \text{if} p=p_{SD}\\ y(p) \text{if} p>p_{SD}\end{cases}}$$
これを供給関数と言い、供給曲線$${y(p)}$$は内点解が最適である限り右上がりとなる。以上の関係を整理すると、以下の図の通りとなる。
なお、最適生産量における条件付要素需要関数は、(無制約の)要素需要関数と呼ばれ、$${d(p, w_v, w_f, \bar x_f)}$$で表す。
$${d(p, w_v, w_f, \bar x_f)\equiv z(s(p, w_v, \bar x_f), w_v, \bar x_f)}$$
また利潤関数は、費用関数を用いて以下のように表すことができる。
$${\pi(p, w_v, w_f, \bar x_f)\equiv ps(p, w_v, w_f, \bar x_f)-C(s(p, w_v, w_f, \bar x_f), w_v, w_f, \bar x_f)}$$
利潤関数の性質は、生産者理論(3)にて議論した通りである。
Hotellingの補題より、供給関数は利潤関数の生産物価格$${p}$$に関する偏導関数であり、要素需要関数は要素価格$${w_i}$$に関する偏導関数となる。
$${\dfrac{\partial}{\partial p}\pi(p, w_v, w_f, \bar x_f)=s(p, w_v, w_f, \bar x_f)}$$
$${\dfrac{\partial}{\partial w_i}\pi(p, w_v, w_f, \bar x_f)=-d_i(p, w_v, w_f, \bar x_f)}$$
Le Chatelierの原理
長期利潤関数を$${\pi(p, w)}$$、短期利潤関数を$${\pi(p, w_v, w_f, \bar x_f)}$$とする。いま、$${(p^*, w^*)}$$の下での長期利潤最大化解を$${x=(x_v^*, x_f^*)}$$とし、以下の関数$${g(p, w)}$$を定義する。
$${g(p, w)\equiv \pi(p, w)-\pi(p, w_v, w_f, x_f^*)}$$
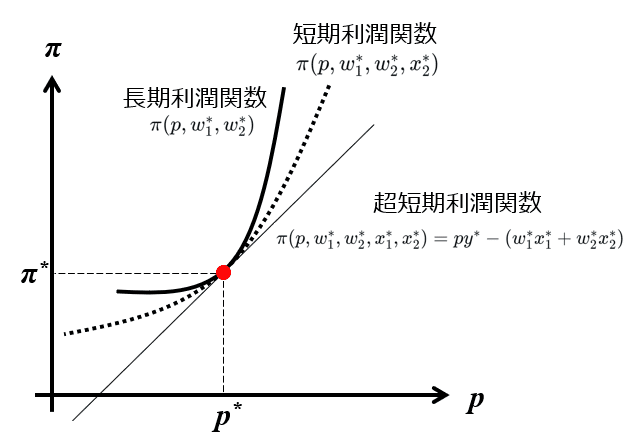
ここで、利潤関数$${\pi}$$は生産物価格$${p}$$に関する凸関数かつ非減少より、以下図のような長期利潤曲線を描ける。いま2生産要素に議論を単純化し、価格体系$${(p^*, w_1^*, w_2^*)}$$における長期利潤最大化解を$${(y^*, x_1^*, x_2^*)}$$とすれば、生産物価格$${p^*}$$において長期利潤曲線と接する直線は、以下のように表せる。
$${\pi(p, w_1^*,w_2^*, x_1^*, x_2^*)=py^*-(w_1^*x_1^*+w_2^*x_2^*)}$$
この直線は全ての生産要素投入量が固定である超短期利潤関数と見なすことができる。同じ価格水準$${p}$$に対し、制約条件の少ない長期の方が利潤が高くなるのは明らかなので、第2要素のみが固定となる短期利潤関数を$${\pi(p, w_1^*,w_2^*, x_2^*)}$$とすると、以下の関係が成り立ち、長期、短期、超短期の利潤曲線の位置関係は以下の図の通りとなる。
$${\pi(p, w_1^*,w_2^*)≥\pi(p, w_1^*,w_2^*, x_2^*)≥\pi(p, w_1^*,w_2^*, x_1^*, x_2^*)}$$
さて、$${g(p, w)}$$の議論に戻ると、以下の不等号関係が成り立つ。
$${g(p, w)≥g(p^*, w^*)=0}$$
つまり、$${g(p, w)}$$は$${(p^*, w^*)}$$において最小値$${0}$$をとる。従って最小の1階条件より、
$${\dfrac{\partial}{\partial p}g(p^*, w^*)=\dfrac{\partial}{\partial p}\pi(p^*, w^*)-\dfrac{\partial}{\partial p}\pi(p^*, w_v^*, w_f^*, x_f^*)=0}$$
また、短期供給関数を$${s(p, w_v, w_f, \bar x_f)}$$と表し、最小の2階条件にHotellingの補題を適用すれば、以下の結果を得る。
$${\dfrac{\partial^2}{\partial p^2}g(p^*, w^*)=\dfrac{\partial}{\partial p}s(p^*, w^*)-\dfrac{\partial}{\partial p}s(p^*, w_v^*, w_f^*, x_f^*)≥0}$$
短期要素需要関数を$${d(p, w_v, w_f, \bar x_f)}$$と表せば同様にして、以下を得る。
$${\dfrac{\partial}{\partial w_i}g(p^*, w^*)=\dfrac{\partial}{\partial w_i}\pi(p^*, w^*)-\dfrac{\partial}{\partial w_i}\pi(p^*, w_v^*, w_f^*, x_f^*)=0}$$
$${\dfrac{\partial^2}{\partial w_i^2}g(p^*, w^*)=\dfrac{\partial}{\partial w_i}d(p^*, w_v^*, w_f^*, x_f^*)-\dfrac{\partial}{\partial w_i}d(p^*, w^*)≥0}$$
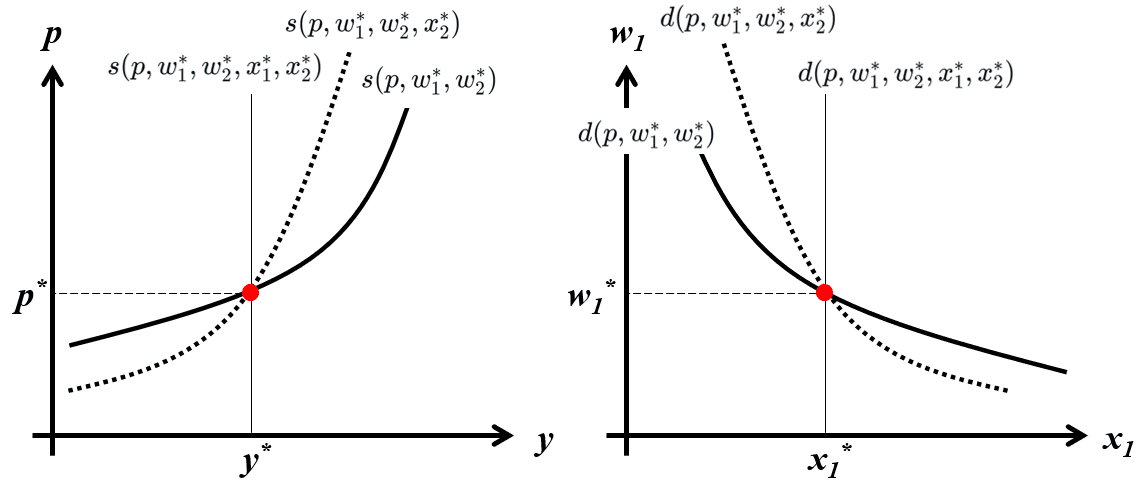
従って以上より、次のLe Chatelierの原理を得る。
Le Chatelierの原理
長期的には、財の供給及び生産要素需要がより弾力的となる
先述の2生産要素モデルより、幾何学的に長期、短期、超短期の供給曲線と要素需要曲線の関係は以下の通り描画できる。
なお、Le Chatelierの原理は以下のコラムのテーマとなっているので併せてご覧頂きたい。歴史的には化学の法則であったこの原理がいかに経済学の理論として成立したか、歴史的経緯を追っている。なお上記のような利潤関数を用いた証明は洗練されており、コラムに記載している素朴な着想からは大きく発展していることが窺える。
次回からは、均衡理論を取り扱う。
