
生産者理論(5):1生産物モデル
今回は、ここまで議論した生産集合の性質や最適化問題をベースに、生産要素と生産物を事前に区別できる場合に用いられる1生産物モデルを導入し、その関数表現となる生産関数の性質を整理する。連載はこちら。
1生産物モデル
生産者は原材料や労働力などの生産要素を市場で購入し、それらを利用して新たな生産物を作り出し、市場で販売する。生産者の選択肢はどの財をどれだけ投入しどれだけ生産するか、その組み合わせに相当する生産計画として表現可能である。
分析対象となる生産者にとって、経済に存在する財の中で$${N}$$種類の生産要素とそれらとは異なる1種類の生産物がある状況を想定し、これを($${N}$$生産要素)1生産物モデルにより表現する。生産要素$${x_i≥0, (i=1, \cdots, N)}$$の投入量と生産物$${y≥0}$$の産出量の組$${(x_1, \cdots, x_N, y) \in \mathbb{R}_+^{N+1}}$$を生産計画という。
1生産物モデルにおいて生産集合$${Y \subset \R_+^{N+1}}$$と産出量ベクトル$${y \in \R_+}$$が与えられたとき、
$${R(y)=\{x \in \R_+^N | (x, y) \in Y\}}$$
と定義される投入ベクトルからなる集合を$${y}$$の必要投入量集合と呼ぶ。これは産出量$${y}$$を実現できる全ての投入ベクトルからなる集合である。また、1生産物モデルにおいて$${Y \subset \R_+^{N+1}}$$と投入量$${x \in \R_+^N}$$が与えられたとき、
$${P(x)=\{y \in \R_+ | (x, y) \in Y\}}$$
と定義される産出量からなる集合を$${x}$$の可能産出量集合と呼ぶ。これは投入ベクトル$${x}$$の下で実現できる全ての生産量からなる集合である。
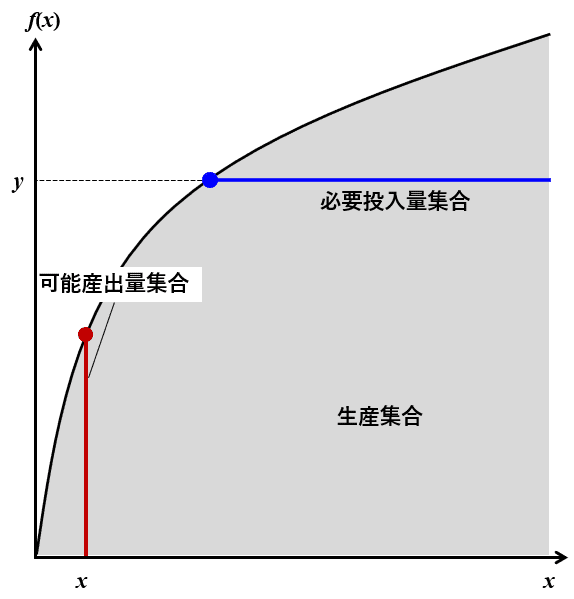
1生産物モデルでは、生産関数を$${y=f(x_1,\cdots, x_N) \equiv f(x)}$$と定義でき、生産集合$${Y}$$や必要投入量集合$${R^*(y)}$$の形状と生産関数$${f}$$の形状との間には、次の関係が成り立つ。
生産集合$${Y}$$や必要投入量集合$${R^*(y)}$$の形状と生産関数$${f}$$の形状との関係
①$${R^*(y)}$$が凸集合$${\Leftrightarrow}$$$${f}$$が準凹関数$${\Leftrightarrow}$$$${y}$$対する上方位集合が凸集合
②$${Y}$$が凸集合$${\Leftrightarrow}$$$${f}$$が凹関数
上記は消費者理論における、選好が凸$${\Leftrightarrow}$$効用関数が準凹$${\Leftrightarrow}$$上方位集合が凸(=無差別曲線が原点に対して凸)の議論と同様に確かめられる。生産集合の凸性の仮定は効用関数の凹性と同値であり、必要投入量集合の凸性よりも強い仮定である。
生産関数の性質
以下では、生産者理論(1)で導入した生産集合の性質について、対応する生産関数$${f}$$の性質に置き換えて記述する。以下断らない限り、生産集合が以下の5つの性質を満たすと仮定する。
①非空:生産関数$${f: \R_+^N \Rightarrow \R_+}$$が存在する
②閉集合:$${f}$$が連続関数
③フリーランチ不可能:$${f(0)=0}$$
④自由可処分:全ての$${x_i}$$について単調非減少かつ$${y \in [0, f(x)]\Rightarrow (x,y) \in Y}$$(=任意の生産計画の右下方部分が$${Y}$$に含まれる)
⑤必要投入量集合の凸性:$${f}$$は準凹関数
短期的に生産要素$${1, \cdots, k< N}$$の投入量が可変、残りの$${k+1, \cdots, N}$$の投入量が固定とする。可変および固定生産要素投入量ベクトルを$${x_v \equiv (x_1, \cdots, x_k) \in \R_+^k, \bar x_f \equiv (x_{k+1}, \cdots, x_N) \in \R_+^{N-k}}$$により表し、短期生産集合$${Y(\bar x_f)}$$を以下の通り定義する。
$${Y(\bar x_f)=\{(x_v, y) \in \R_+^{k+1} | (x_v, \bar x_f, y) \in Y\}}$$
いずれの投入要素も可変的と見なせる長期的な生産計画を考える場合には、以下の無生産の可能性を仮定することがある。短期的に投入要素が固定された生産要素がある場合や、長期的にも投入量のうち回収できない部分(埋没費用)がある場合にはこの仮定は成り立たない。
無生産の可能性:$${(0,0) \in Y}$$
⑤の必要投入量集合の凸性については、しばしばより制約的な生産集合の凸性、また長期的な生産集合に関しては、更に制約的な生産集合の可分・加法性まで仮定されることがある。
生産集合の凸性:$${f}$$は凹関数
生産集合の可分・加法性:$${f}$$は1次同次の凹関数
規模に対する生産性に関する性質も、1生産物モデルの場合は、以下のように定義するのが一般的である。
収穫逓増:$${f(0)=0}$$かつ任意の$${t>1}$$に対して$${f(tx)>tf(x)}$$
収穫逓減:$${f(0)=0}$$かつ任意の$${t>1}$$に対して$${f(tx)< tf(x)}$$
収穫一定:$${f(0)=0}$$かつ任意の$${t>0}$$に対して$${f(tx)=tf(x)}$$

限界生産性と技術的限界代替率
限界生産性
生産者の技術が生産集合$${Y \subset \mathbb{R}_+^{N+1}}$$および生産関数$${f: \mathbb{R}_+^{N}\rightarrow \mathbb{R}_+}$$として表現される時、投入ベクトル$${\bar x \in \mathbb{R}_+^{N}}$$と生産要素$${i (=1, \cdots, N)}$$を任意に選ぶと、点$${\bar x}$$における生産要素$${i}$$の限界生産性$${MP_i(\bar x)}$$を次のように定義する。
$${MP_i(\bar x)=\dfrac{f(\bar x_1, \cdots, \bar x_i + \Delta x_i, \cdots, \bar x_N)-f(\bar x)}{\Delta x_i}}$$
$${f}$$が点$${\bar x}$$において偏微分可能である場合は十分小さい$${\Delta x_i}$$について、以下の近似関係が成立する。
$${f(\bar x_1, \cdots, \bar x_i + \Delta x_i, \cdots, \bar x_N)≈f(\bar x)+\dfrac{\partial f(\bar x)}{\partial x_i}\Delta x_i}$$
従って、十分小さい$${\Delta x_i}$$について以下の関係が成り立つ。
限界生産性:$${MP_i(\bar x)=\dfrac{\partial f(\bar x)}{\partial x_i}}$$
通常、限界生産性については以下の性質が仮定される。
$${MP_i(x)=\dfrac{\partial f(x)}{\partial x_i}≥0}$$
$${\dfrac{\partial}{\partial x_i}MP_i(x)=\dfrac{\partial^2 f(x)}{\partial x_i^2}<0}$$
つまり他の生産要素の投入量を固定したまま生産要素$${i}$$の投入量を増加させたとき、生産物の産出量は非減少だが、産出量の増分は小さくなっていくことを意味する。この仮定が成立する場合、生産要素$${i}$$に関する限界生産性逓減の法則(または収穫逓減の法則)が成り立つという。限界生産性逓減の法則は「特定の」生産要素の投入量のみ変化させた場合の産出量の変化に関する性質であり、「全ての」生産要素の投入量を同時に変化させた場合の産出量の変化に関する性質である規模に関する収穫逓減とは区別する必要がある。
技術的限界代替率
$${\bar x}$$を出発点として生産要素$${i}$$の投入量を$${\Delta x_i}$$だけ変化させたときに、産出量$${f(\bar x)}$$を維持するために別の生産要素$${j}$$の投入量を$${\Delta x_j}$$だけ変化させる必要がある場合、
$${f(\bar x_i, \cdots, \bar x_i+\Delta x_i, \cdots, \bar x_j + \Delta x_j, \cdots, \bar x_N)=f(\bar x)}$$
が成り立つ。この時、以下のように$${\bar x}$$における生産要素$${i}$$の生産要素$${j}$$で測った技術的限界代替率を定義する。
$${MRTS_{ij}(\bar x)=-\dfrac{\Delta x_j}{\Delta x_i}}$$
$${f}$$が点$${\bar x}$$において全微分可能である場合は十分小さい$${\Delta x_i}$$と$${\Delta x_j}$$について、以下の近似関係が成立する。
$${f(\bar x_i, \cdots, \bar x_i+\Delta x_i, \cdots, \bar x_j + \Delta x_j, \cdots, \bar x_N)\\≈f(\bar x)+\dfrac{\partial f(\bar x)}{\partial x_i}\Delta x_i+\dfrac{\partial f(\bar x)}{\partial x_j}\Delta x_j}$$
産出量維持の条件から$${f(\bar x_i, \cdots, \bar x_i+\Delta x_i, \cdots, \bar x_j + \Delta x_j, \cdots, \bar x_N)≈f(\bar x)}$$とすれば、
$${\dfrac{\partial f(\bar x)}{\partial x_i}\Delta x_i+\dfrac{\partial f(\bar x)}{\partial x_j}\Delta x_j≈0}$$
となる。従って十分小さい$${\Delta x_i}$$と$${\Delta x_j}$$について以下の関係が成り立つ。
$${\bar x}$$における生産要素$${i}$$の生産要素$${j}$$で測った技術的限界代替率:
$${MRTS_{ij}(\bar x)=\dfrac{\dfrac{\partial f(\bar x)}{\partial x_i}}{\dfrac{\partial f(\bar x)}{\partial x_j}}}$$
所与の投入ベクトルの下で最大の産出量を実現しようとする生産者が投入ベクトル$${\bar x}$$に直面した時、この生産者の技術の下では、1単位の生産要素$${i}$$は$${MRTS_{ij}(\bar x)}$$単位の生産要素$${j}$$と実質的に等しく、両者を交換しても産出量は$${f(\bar x)}$$のまま不変である。この比例関係から、$${MRTS_{ij}(\bar x)}$$と$${MRTS_{ji}(\bar x)}$$は互いに逆数の関係にある。
$${MRTS_{ij}(\bar x)=\dfrac{1}{MRTS_{ji}(\bar x)}}$$
ここで、技術的限界代替率の幾何学的解釈のため、2生産要素1生産物モデルを考える。生産関数$${f:\mathbb{R}_+^2 \rightarrow \mathbb{R}_+}$$が与えられたとき、投入ベクトル$${(\bar x_1, \bar x_2) \in \mathbb{R}_+^2}$$に対応する等量曲線は、
$${R^*(\bar x_1, \bar x_2)=\{(x_1, x_2) \in \mathbb{R}_+^2 | f(x_1, x_2)=f(\bar x_1, \bar x_2)\}}$$
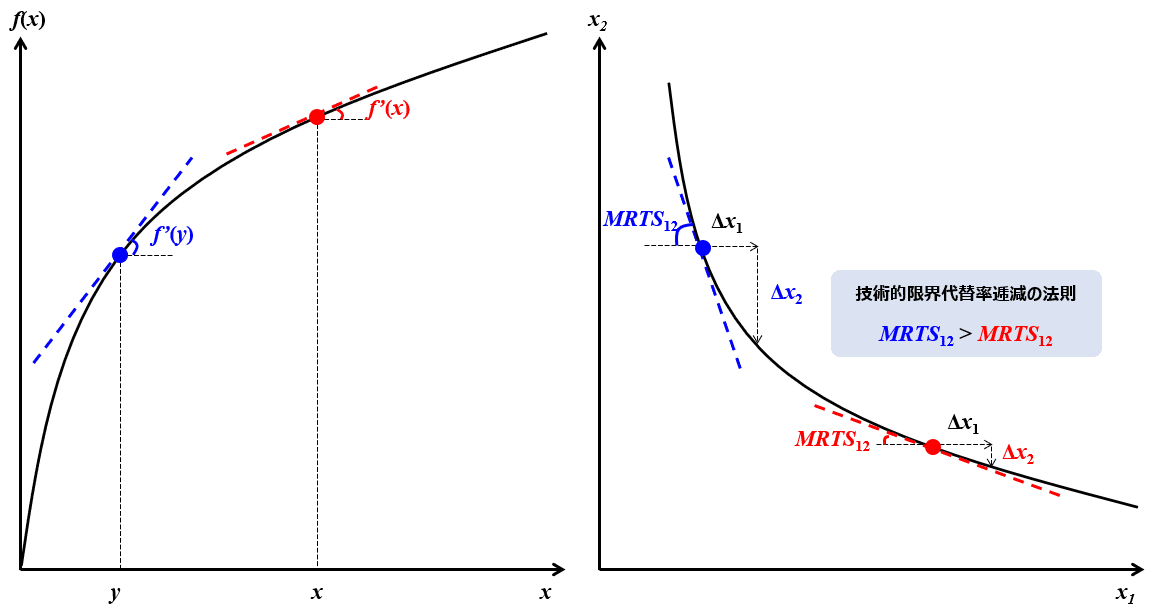
と定義される。技術的限界代替率$${MRTS_{12}(\bar x_1, \bar x_2)}$$は幾何学的には、産出量$${f(\bar x_1, \bar x_2)}$$に対応する等量曲線$${R^*(\bar x_1, \bar x_2)}$$上の点$${(\bar x_1, \bar x_2)}$$における接線の傾きの大きさに等しい(消費者理論の限界代替率に関する議論も参照)。ここで、$${R^*(x)}$$に属する異なる2つの投入ベクトル$${x, y \in R^*(x)}$$において、
$${x_i< y_i \Rightarrow MRTS_{ij}(x)>MRTS_{ij}(y)}$$
が成り立つ時、技術的限界代替率逓減の法則が成り立つという。この法則を仮定することは、産出量を一定に保ったまま生産要素$${i}$$の投入を増やした場合、生産要素$${i}$$によって他の生産要素$${j}$$を代替していくことが次第に困難になることを意味する。
生産関数の形状との関係
以下では、2生産要素1生産物モデルを用いて生産関数の形状と、生産技術が通常満たすであろう様々な性質との関係を議論する。生産関数が凹関数であると仮定することにより、規模に対する収穫非増加、限界生産性逓減の法則、技術的限界代替率逓減の法則を導くことができる。
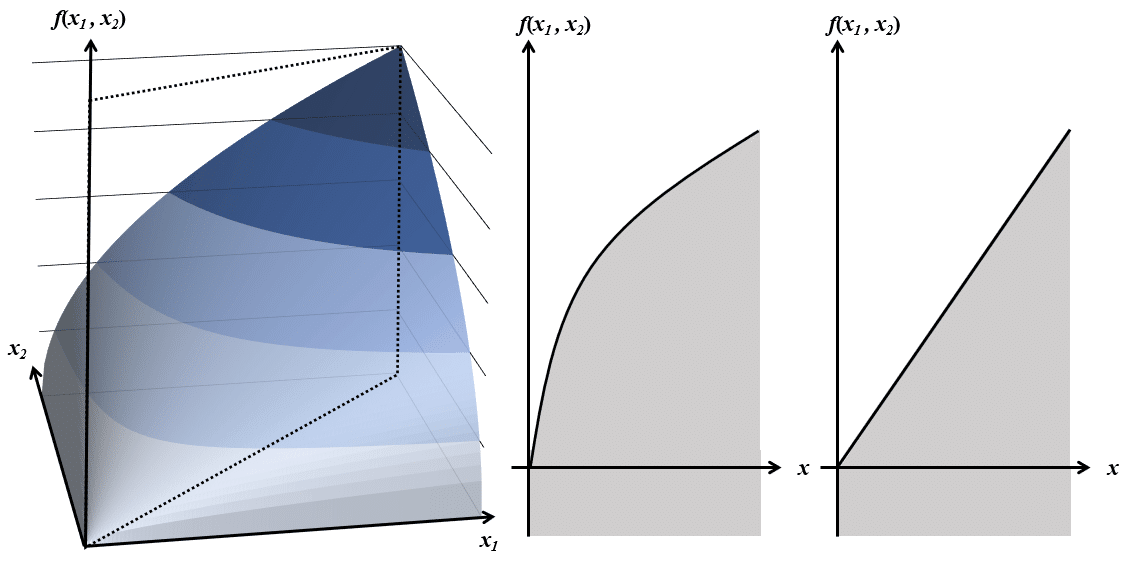
$${f(x_1, x_2)}$$を長期生産関数として、原点を通る平面で切った時、断面の形状から規模に対する収穫非増加(収穫逓減もしくは一定)を表現可能
$${f}$$を$${x_2}$$軸に垂直な平面($${x_2 = Const.}$$)で切った時の短期生産関数$${f(x_1)}$$において、$${x_1}$$の限界生産性逓減の法則を表現可能
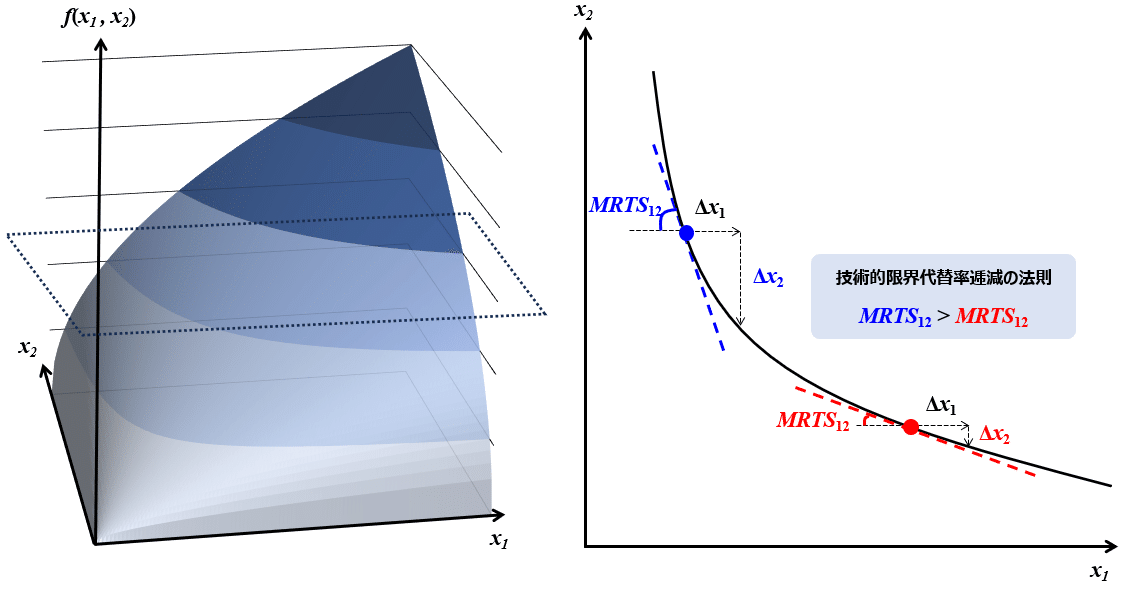
$${f}$$を$${x_1-x_2}$$平面に平行な平面で切った時、等量曲線は原点に対して凸であり、技術的限界代替率逓減の法則を表現可能
以上の関係を図示すると、以下の通りである。

次回はこちら。
この記事が気に入ったらサポートをしてみませんか?
