正多面体「正多面体は正四面体、立方体、正八面体、正十二面体、正二十面体の５つだけ」「正ｎ面体の各面を、互いに異なるｎ色すべてを使って塗り分ける方法の数は、正ｎ面体がｎ個の正ｍ角形で構成されるとして、ｎ！／（ｎ×ｍ）通り」

オンライン家庭教師はじめました。
ご興味がおありでしたら、
①以下のホームページへアクセス、
https://man2man.jp/service/ワンセンテンス算数の算数（マンツーマン）/
②ユーザー登録（ユーザー登録はこちらから）ののち、
③上記ホームページの下の方に私宛のメッセージ機能（STEP１として「ワンセンテンス算数さんにメッセージを送る」というボタン）がありますので、そちらからお問い合わせください。

前回まで、正四面体、立方体（正六面体）とみてきました。正四面体、立方体（正六面体）は、正多面体とよばれる立体に分類されます。
では、正多面体とはどのような立体をいうのでしょうか。

それは、
①すべての面が同一の正多角形でできている
②すべての頂点に集まる面の数が等しい
③へこんでいない
という、３つの条件を満たす対称性の高い立体をいいます。

具体的には以下の５つしかありません。

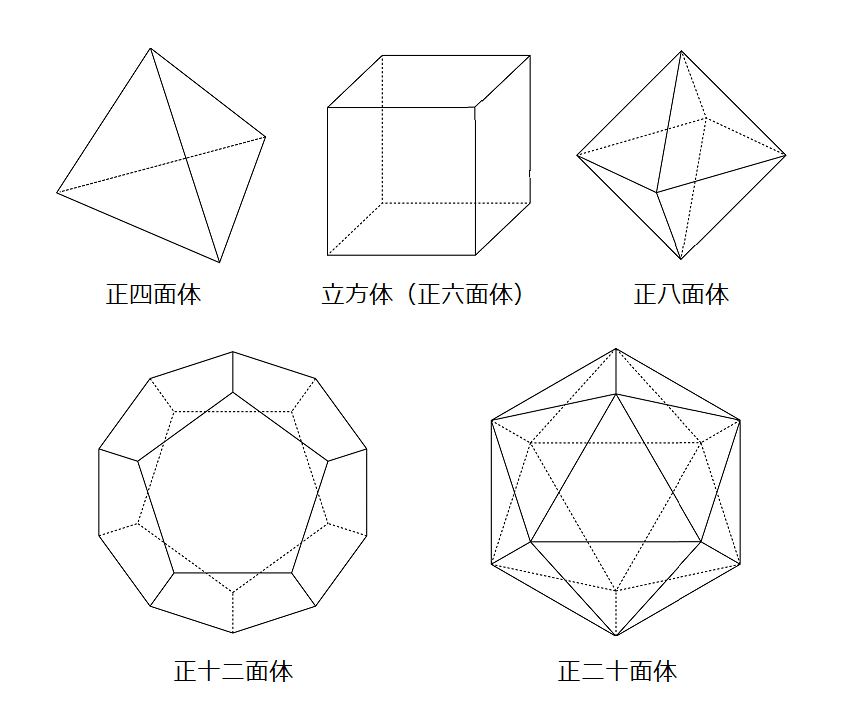
注　例えば、正四面体を２つくっつけた立体は②の条件から、また例えば、正二十面体の一部をへこませたような立体は③から、正多面体ではありません。

小学生なので、ここまでで十分です。

ただ、せっかく正四面体、立方体と、塗り分けの問題を解決してきましたから、すべての正多面体についても考えておきましょう。

問題
正ｎ面体の各面を、互いに異なるｎ色すべてを使って塗り分ける方法は何通りあるでしょうか。但し、正ｎ面体を回転させたとき面の色が一致する塗り方は、同じ塗り方として１通りとします。