
Python でピタゴラス数を書き出す
a²+b²=c² を満たす自然数 a , b , c の組み合わせを ピタゴラス数 と言います。三角形の3辺の長さ (a,b,c) がこの式を満たすとき、その三角形は直角三角形になります。
さて、Pythonでプログラムを作って「100以下のピタゴラス数」を全部書き出してみましょう。
次のように3重ループを作って、a,b,c をそれぞれ 1 から 100 まで回せばとりあえず出てきます。
for a in range(1,100):
for b in range(1,100):
for c in range(1,100):
if a*a+b*b==c*c:
print(a,b,c)でも、このままではいくつかの難点があります。
① (3,4,5) と順番が違うだけの (4,3,5) が出てくる。(合同な三角形)
② (3,4,5) の整数倍 (6,8,10) などが出てくる。(相似な三角形)
③ 表示される順番が不自然。(13,84,85) の後に (20,21,29) が出てくる。
④ 大きい数まで出そうとすると時間がかかりすぎる。
では、上のプログラムを書き換えて、どれでも良いので、解決してください。どれか1つだけでも良いので、改善してください。
◇ ◇ ◇
①と③を解決するには、次のように書き換えれば良い。演算回数が減る分、多少は時間の節約にもなるでしょう。
for c in range(1,100):
for b in range(1,c):
for a in range(1,b):
if a*a+b*b==c*c:
print(a,b,c) 次に②の解決を図りましょう。これがなかなか難しいのですが、頑張ってください。
次のプログラムでは、ピタゴラス数を表示するのに加えて、小さい順に番号を振りながら、個数を数えました。
count=0
for c in range(1,100):
for b in range(1,c):
for a in range(1,b):
if a*a+b*b==c*c:
check=1
for i in range(2,a):
if a%i==0 and b%i==0 and c%i==0:
check=0
if check==1:
count=count+1
print(count,' ',a,b,c)
print('fin')これを実行した結果は、次の通りです。あっという間に表示されます。全部で 16 組ありました。
1 3 4 5
2 5 12 13
3 8 15 17
:
15 39 80 89
16 65 72 97
fin
さて「100以下のピタゴラス数」なら上のプログラムですぐに出ますが、もっと大きい数まで、例えば「10,000以下のピタゴラス数」を表示しようとすると、上のプログラムでは時間がかかりすぎます。
というのは、「○○以下のピタゴラス数」と言うときの○○に入る数がn倍になると、a,b,c に入れるパターンがそれぞれn倍になりますから、3文字の組み合わせで演算回数は n³ 倍になるのです。
ですから「1,000まで」を表示するには「100まで」の場合の 10³=千倍、「10,000まで」を表示するには「100まで」の場合の 100³=百万倍の時間がかかると、ざっくり言えばそういうことになるわけです。
それはそうと、上のプログラムのまま「1,000以下のピタゴラス数」を表示させてみたところ、ちょっとしたことに気がつきました、ピタゴラス数が現れる頻度です。「1,000以下のピタゴラス数」は全部で 158 組あったのですが、100ごとに区切って数えると結果は次の通りでした。
範囲 個数 増加分
~ 100 16 16
~ 200 32 16
~ 300 47 15
~ 400 63 16
~ 500 80 17
~ 600 95 15
~ 700 112 17
~ 800 128 16
~ 900 140 12
~ 1000 158 18
演算回数=所要時間=候補 が 2³=8 倍、3³=27 倍、4³=64 倍、… と3乗で増えていくのに、ピタゴラス数の出現回数は2倍、3倍、4倍とほぼ比例しているように見えるんですね。
となると、俄然「10,000まで」やってみたくなりますね。時短プログラムを作って、うまくいったらついでに「ピタゴラス数の出現頻度」を調べたい。
というわけで、やってみました。その結果、けっこう短い時間で「10,000まで」表示できて、「100個ごと」に区切って数えて、あわせて Python の勉強のためにグラフ化までやってみました。
import matplotlib.pyplot as plt
n=10000
count=[]
for i in range(int(n/100)):
count.append(0)
for c in range(1,n):
for b in range(1,c):
a=int((c*c-b*b)**(1/2))
if a<b:
if a*a+b*b==c*c:
i=2
while i<a and (a%i!=0 or b%i!=0 or c%i!=0):
i=i+1
if i==a:
j=int(c/100)
count[j]=count[j]+1
print(a,b,c)
sum=0
for i in range(int(n/100)):
sum=sum+count[i]
plt.scatter(i*100,sum)
print(i*100,'~',(i+1)*100,' ',count[i],' ',sum)
plt.show()その結果、全部で 1593 組のピタゴラス数が表示されて、その最後の行は
2772 9605 9997
でした。
また、上限「100ごと」に区切って数えた「ピタゴラス数の出現頻度」は次の通りで、ほぼ直線状になりました。
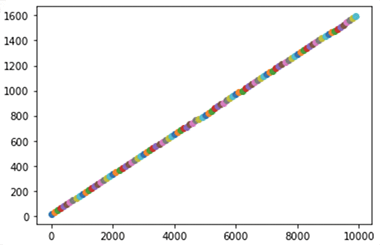
繰り返しますが、「1,000まで」のピタゴラス数を調べるには「100まで」の場合と比べて演算回数≒所要時間は 10³=千倍もかかるのに、その出現回数はたったの10倍で、「10,000まで」のピタゴラス数を調べるには「100まで」の場合と比べて演算回数≒所要時間は 100³=百万倍もかかるのに、その出現回数はやっぱり100倍。実際のところ「100まで」で 16 個、「1,000まで」で 158 個、「10,000まで」で 1593 個でした。
私としては意外な結果なのですが、皆さんはどうお感じでしょうか。
◇ ◇ ◇
〜 Python で2重ループ・3重ループ 〜
▷ Python が九九81匹
▷ Python で素因数分解する
▷ Python でピタゴラス数を書き出す
