数列　公式をほぼ教えない授業実践・プリント準備少なめ

　数列は，教科書を見ると，公式主体の単元という印象があります。しかし公式主体だと，生徒の頭は鍛えられませんし，何より面白くありません。この記事では，公式をほぼ教えない授業実践を紹介します。
　プリントの準備が少なくて済むので、経験の浅い教師にも実践しやすいです。多分。

１．等差数列の一般項

　まず，何の予備知識もなく，以下の問題を生徒に投げます。等差数列は，中学受験の世界では小３の内容で，高校生がちゃんと考えればこの程度の問題は解けます。

　ここで自分が話しているのは，

①等差数列の定義
②初項・公差 (以下 d と表す) の定義
③21番目といっても，d は 21 回たすのではないよ。こういうずれを，植木算というよ。指 5 本だと，あいだは 4 つだよね。わからなかったら，自分の手を見て考えよう。
④ a(60)-a(50)=d(60-50) だよね。こう考えると，(2) は a(21)=a(1)+d(21-1) となるね。このあたりも，混乱してきたら数列を並べて書いて，ずれが起きていないかを確認しよう。

ぐらいです。以上の内容は，公式化しません。あとは問題にどんどんあたらせます。「a(3)=11，a(6)=17 」も，例題として扱わず，生徒にやらせましょう。で，生徒が解けなかったり間違えたら生徒が修正すればいいんです。生徒が問題が解けない可能性を，先回りして全部つぶそうとするのは，特にこの単元では控えたほうがいいでしょう。重要なのは，とにかく教師が数列を書き並べて，視覚的に説明すること。そして，生徒が問題を視覚化するように促すことです。

　細かい技術論です。初項は a(1) と書くほうが筋が通ると感じます。例えば a(3)=11，a(6)=17 のときは，(6-3)d=17-11 から d=2 より，a(n)=a(3)+2(n-3) と，初項を求めずに解決します。なお，お気づきのことと思いますが，これは直線の方程式に他なりません。どこかの段階で，等差数列が n の一次関数になることは触れたほうがいいでしょう。また，等差中項ですが，ナニソレオイシイノ？　等差数列の共通項を見つける問題については，「根性で書き出せばわかるよ」で OK。

２．等差数列の和

　これも，問題を投げるところからです。意外に，中学受験をやっていなくても，生徒は解けますよ。

　いろいろな解答が出てきます。生徒の戦略としては，偶数個の和ならペアを作る，というものが多いです。「実は，平均を使えば奇数個のときもうまくいくので，求め方に場合分けが入らなくなるよ」って自分は持っていってます。(2) では，S=5+7+9+11+13=9+9+9+9+9 になることを生徒と確認し，「平均×個数」で求まることを話します。また，その平均は，例えば初項と末項の平均で求まることを (3) で確認します。

　以上の内容は，公式化しません。あとは，問題をどんどん解かせます。ある程度練習をすると，平均を初項と末項から求めるように頭が固定される生徒が多いので，
「a(5)=7, S(5)=？」や「a(4)=7,  a(5)=9, S(10)=？」あたりで，再度頭をマッサージしてやります。

　細かい技術論です。「a(1)=50,  d=-3,  のとき，S(n) の Max は？」という有名問題については，「S(n)=50+47+44+… ，この続きを 20 個も書けばわかるよ～」と，優しくぶん投げましょう。
　あと，「S(10)=3,  S(20)=8,  S(30)=？」では，
　　T(1)=a(1)+a(2)+…+a(10),
　　T(2)=a(11)+a(12)+…+a(20), 
　　T(3)=a(21)+a(22)+…+a(30),
とすると，T(1), T(2), T(3) が等差数列をなすことは，生徒と一緒に確認したいところです。

３．等比数列の一般項

　次の問題を投げます。もうすでに根幹は押さえてあるので，これは教科書の例題を使ってもいいでしょう。やることは等差数列と同じなので，等比数列の定義，公比を r と書くよ，ということだけ確認して，あとは問題解きまくりで OK です。

４．等比数列の和

　等比数列の和には公式がありますが，少なくとも数列触りたての生徒には，公式は教えないようにしています。「S と rS を並べてみろ。そうするとわかるよ」とだけ言って，あとは生徒に任せましょう。

　あと，「S(10)=3,  S(20)=6,  S(30)=？」では，
　　T(1)=a(1)+a(2)+…+a(10),
　　T(2)=a(11)+a(12)+…+a(20), 
　　T(3)=a(21)+a(22)+…+a(30),
とすると，T(1), T(2), T(3) が等比数列をなすことは，生徒と一緒に確認したいところです。

５．Σr^k，Σ(ak+b)

　ここで話すことは，「シグマは並べろ」だけです。「並べれば，今までと同じだよね」。一次式が等差数列になることは，いろんなアプローチで繰り返し話します。
　余力があれば，次の布石として，Σr^k を 〇Σ(r^k-r^(k-1)) の形に変形する話もします。

６．Σk^2，Σk^3 （※未実践）

　すど氏（@ysmemoirs）から，この公式を天下りで与えるのではなく，発見させるアプローチを教わりましたので，それをもとに教案を作ってみました（つまり，まだ実践してません）。まず，以下の作業をやらせます。

　U(n)={S(n)}^2 は，すぐに見つかると思います。問題は T(n) ですが，次の感じで予想させてみます。これで，T(n)=S(n)×(2n+1)/3 が見えます。予想さえ立てば，証明は例えば T(k)-T(k-1)=k^2 のように瞬間です。

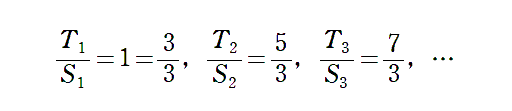
７．Σ の線形性

　「シグマは並べろ」で，手を動かして線形性を理解させます。特に，下の 3 つ目の式が間違いの宝庫で，1 回では定着しないにせよ，まずは初回をここで話します。　

　以上の内容は，公式として板書はしません。忘れたら，並べるだけ。

８．階差数列の利用

　階差数列の定義はちゃんと説明しますが，あとは下のような感じで進めます。

　以上です。