続「『ChatGPT-READYな社会』のために必要な教育カリキュラム」の考察と108の授業アイデア。

前回記事

前回は3時間25チャット制限のため中断しました。

75-108の授業アイデア

75.AIを使ったコミュニケーションスキル学習: ChatGPTを使って、効果的なコミュニケーション方法やリスニングスキルを学ぶ授業。
76.AIとの共同音楽制作: ChatGPTを使って、オリジナルの曲を作曲し、演奏する授業。
77.AIを使った体力測定: ChatGPTを使って、各種運動能力を測定し、運動プランを立てる授業。
78.AIとの共同マナー学習: ChatGPTを使って、礼儀やマナーに関する知識を学ぶ授業。
79.AIを使った緊急時対策学習: ChatGPTを使って、地震や火事などの緊急時に対処する方法を学ぶ授業。
80.AIとの共同健康管理: ChatGPTを使って、日々の食事や運動による健康管理方法を学ぶ授業。
81.AIを使ったアニメーション制作: ChatGPTを使って、オリジナルのアニメーションを制作する授業。
82.AIとの共同実験室: ChatGPTを使って、科学実験の手順や結果を解析する授業。
83.AIを使ったデザイン学習: ChatGPTを使って、グラフィックデザインやロゴデザインの基本を学ぶ授業。
84.AIとの共同料理研究: ChatGPTを使って、食材の特徴や組み合わせ方を学び、新しいレシピを考案する授業。
85.AIを使ったマジック学習: ChatGPTを使って、手品やマジックの仕組みを学び、実際にマジックを披露する授業。

86.AIとの共同環境保護活動: ChatGPTを使って、環境問題について学び、環境保護のためのアクションプランを立てる授業。
87.AIを使った建築学習: ChatGPTを使って、建築物の構造やデザインの基本を学ぶ授業。
88.AIとの共同公共サービスプロジェクト: ChatGPTを使って、地域の公共サービスやインフラに関する提案を考える授業。
89.AIを使った海洋学習: ChatGPTを使って、海洋生物や海の環境について学ぶ授業。
90.AIとの共同映画制作: ChatGPTを使って、オリジナルの映画のシナリオを作成し、実際に撮影する授業。
91.AIを使った経済学習: ChatGPTを使って、経済の基本概念や市場の仕組みを学ぶ授業。
92.AIとの共同エネルギー研究: ChatGPTを使って、持続可能なエネルギー源に関する研究を行う授業。
93.AIを使った都市計画学習: ChatGPTを使って、都市計画や交通網の仕組みを学ぶ授業。
94.AIとの共同農業プロジェクト: ChatGPTを使って、農業技術や作物の栽培方法を学ぶ授業。
95.AIを使った自動車工学学習: ChatGPTを使って、自動車の構造や動力源について学ぶ授業。
96.AIとの共同ロボット工学プロジェクト: ChatGPTを使って、ロボットの設計や制御方法を学ぶ授業。
97.AIを使った言語学習: ChatGPTを使って、外国語や言語学の基本概念を学ぶ授業。
98.AIとの共同アートアプリシエーション: ChatGPTを使って、アート作品の鑑賞や評価方法を学ぶ授業。
99.AIを使った天文学習: ChatGPTを使って、天文学の基本概念や星座の観察方法を学ぶ授業。

(飽きてきたなぁ。つまらんなぁ。)
100-104は国語もしくは言語に関する内容に限定してみましょう。

100.AIを使った古典文学の解釈: ChatGPTを使って、古典文学作品の背景やテーマ、登場人物の性格分析を学ぶ授業。
101.AIとの共同俳句・短歌制作: ChatGPTを使って、俳句や短歌の基本的なルールを学び、実際に作品を作成する授業。
102.AIを使った漢字学習: ChatGPTを使って、漢字の成り立ちや意味、音訓のルールを学ぶ授業。
103.AIとの共同言葉の起源探求: ChatGPTを使って、日本語や外国語の言葉の起源や語源を学ぶ授業。
104.AIを使った文章添削・指導: ChatGPTを使って、生徒が作成した文章を添削し、効果的な表現方法や語彙の使い方を指導する授業。

105-108は数や図形に関する内容で考えましょう。

105.AIを使った算数のパズル解決: ChatGPTを使って、算数に関連するパズルや問題を解決するためのアプローチや解法を学ぶ授業。
106.AIとの共同幾何学的アート制作: ChatGPTを使って、幾何学的な図形を用いたアート作品を制作する授業。
107.AIを使った図形の性質探求: ChatGPTを使って、三角形や四角形などの図形の性質や定理を学ぶ授業。
108.AIとの共同数学パターン探索: ChatGPTを使って、数列やフラクタルなどの数学的パターンを探求する授業。

(これらをもっとはやくやればよかったなと。)

106.「AIとの共同幾何学的アート制作」の具体的な授業の流れ

106「AIとの共同幾何学的アート制作」の具体的な授業の流れを考えてみましょう。

AIとの共同幾何学的アート制作:

授業の目標説明:
教師が授業の目標を説明し、幾何学的アートの例を紹介する。
幾何学的アートの基本知識:
教師が幾何学的アートに関する基本知識を解説し、さまざまな幾何学的アートの種類や特徴を紹介する。
AI（ChatGPT）の紹介:
教師がChatGPTの機能と活用方法を説明する。
ブレインストーミング:
生徒たちが、どのような幾何学的アートを制作したいかを考え、アイディアを出し合う。
ChatGPTとのコラボレーション:
生徒たちはChatGPTにアイディアを入力し、アート作品の具体的なデザインや構成に関する提案を得る。
デザインのスケッチ:
生徒たちはChatGPTの提案をもとに、デザインのスケッチを作成する。
実際の制作:
生徒たちはペンや紙、絵の具、デジタルツールなどを使って、スケッチに沿って幾何学的アート作品を制作する。
作品の発表:
生徒たちは制作した幾何学的アート作品をクラスで発表し、他の生徒からのフィードバックを受ける。
AI（ChatGPT）による評価:
生徒たちはChatGPTに作品を提示し、アート作品に対する評価や改善点を得る。
授業のまとめと今後の展望:
教師が授業を振り返り、幾何学的アート制作におけるAIの活用や今後の学習について話す。

このような流れで、AIとの共同幾何学的アート制作の授業が進められます。生徒たちは幾何学的アートの基本知識を学びながら、AIを活用して独自のアート作品を制作する経験を通じて、創造力と協働力を養うことができます。

では、108という数字を生かした幾何学アートを作りたいのですが、どんなことができそうですか。

108という数字を生かした幾何学アートのアイディアをいくつか提案します。

円周上の108の点: 円周上に等間隔で108の点を配置し、点同士を異なるパターンで線で結ぶことで、美しい幾何学的模様を作成します。

108度の回転対称性: 108度の回転対称性を持つ図形を用いて、独自の幾何学的アートを作成します。例えば、ペンローズタイリングのような図形を用いて、108度の回転対称性を持つアート作品をデザインします。

108角形のタイリング: 正108角形を使って、平面をタイリング（敷き詰める）パターンを作成します。さらに、色やテクスチャを使って、視覚的に魅力的なアート作品を制作します。

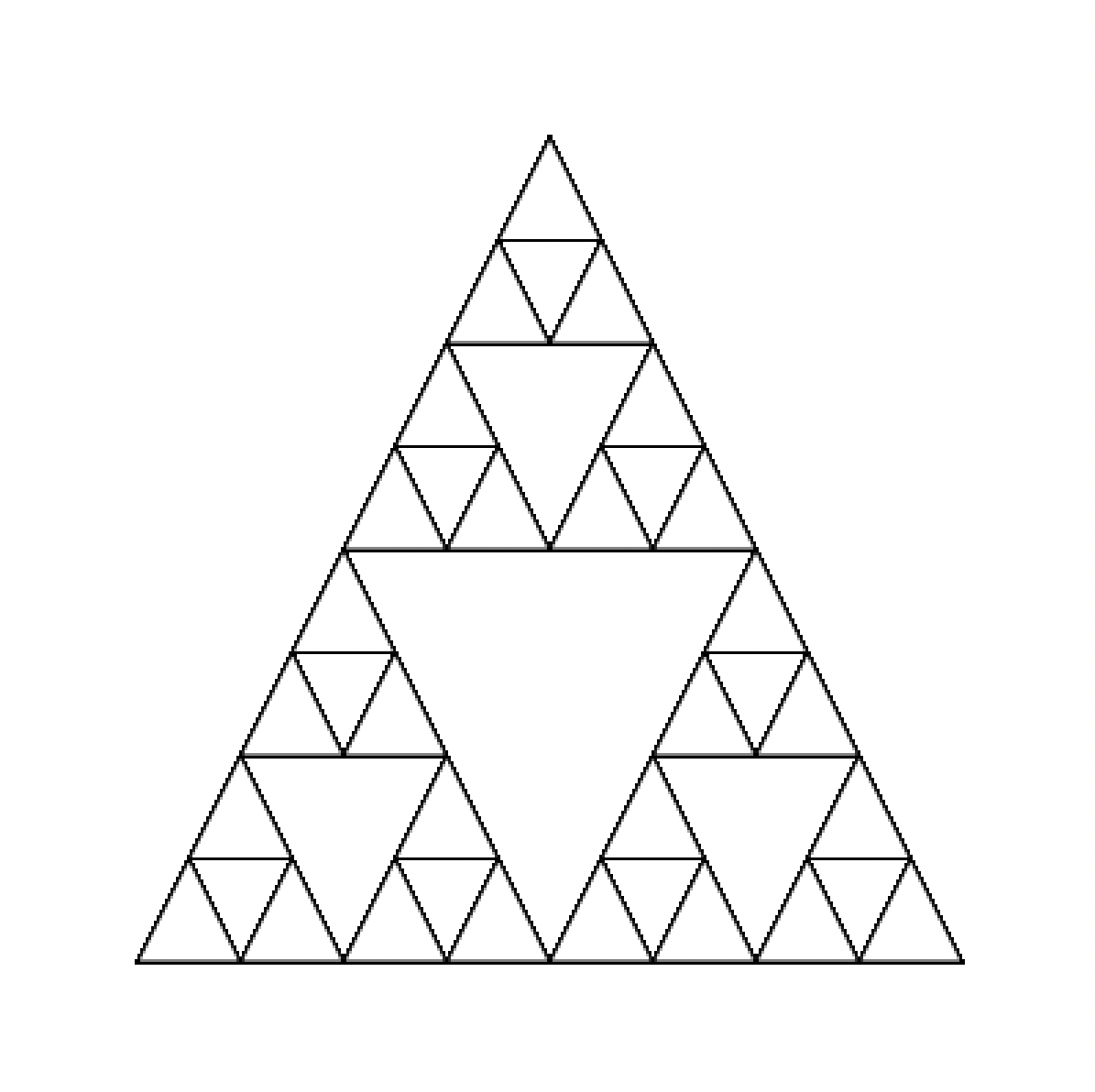
108層のフラクタル構造: 108層のフラクタル構造を持つ幾何学的アートを作成します。例えば、シェルピンスキーの三角形やマンデルブロット集合のようなフラクタル図形を108層に発展させ、複雑で美しいアート作品をデザインします。

数字108の幾何学的表現: 数字108を構成する各数字（1、0、8）の幾何学的表現を作成し、それらを組み合わせて独自のアート作品をデザインします。例えば、1を直線、0を円、8を2つの重なった円として表現し、それらを組み合わせた幾何学的デザインを作ります。
これらのアイディアを参考に、108という数字を生かした幾何学アート作品を制作してみてください。創造力を発揮し、独自のアート作品を楽しんでください。

5つの案それぞれをprocessingのコードで書いてください。

Processingを用いた5つのアイディアの実装例を提供します。実行するには、Processing IDEで新しいスケッチを作成し、以下のコードをコピー＆ペーストして実行してください。

円周上の108の点:

108度の回転対称性

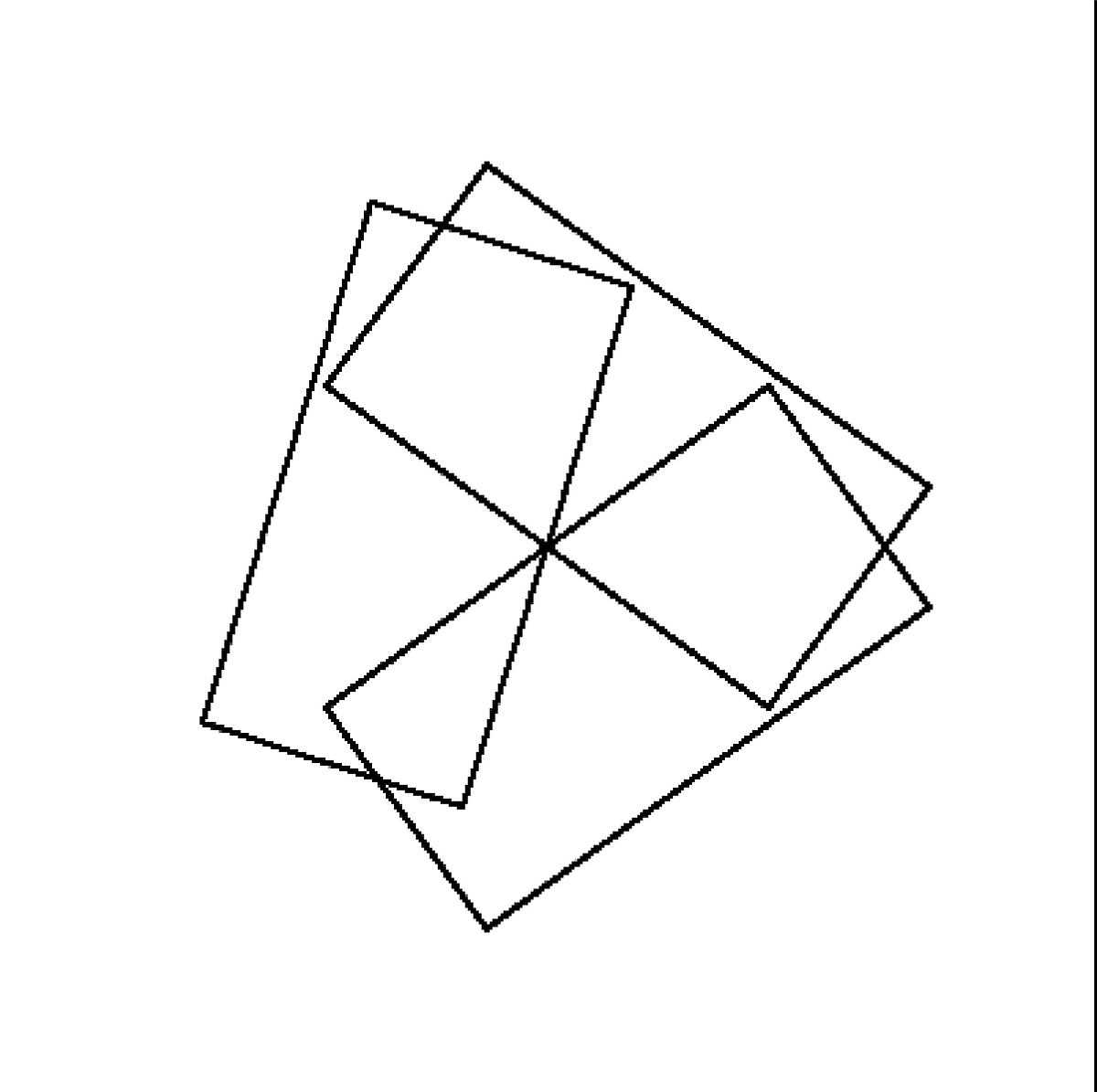
108角形のタイリング:

時々こうやってしくじりますよね。

108層のフラクタル構造は、処理速度や描画の制約のため、現実的ではありません。その代わり、3層のシェルピンスキーの三角形を描画します。

この後試したところ11が私は描画限界でした。画像は3

数字108の幾何学的表現:

これお気に入り

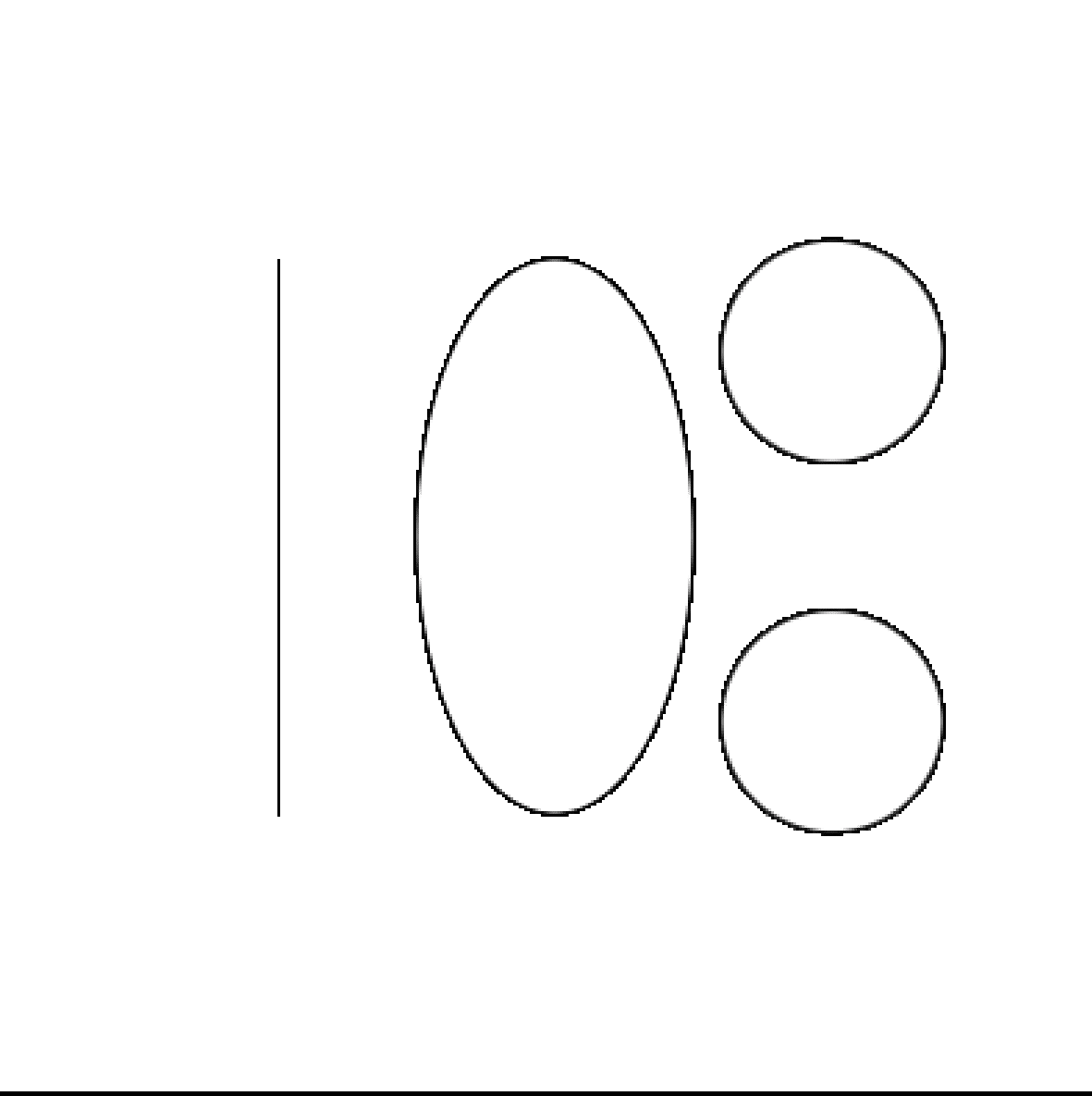
これらのコードはProcessing IDEで実行できます。アート作品に必要なカスタマイズを行い、独自のデザインをお楽しみください。

数字108の幾何学的表現に規則的な動きを加えたいです

数字108の幾何学的表現に規則的な動きを加える方法として、円や線の位置や大きさを時間に応じて変化させることができます。以下のコードは、円の大きさをサイン波に沿って変化させ、縦線の位置を左右に揺らす実装例です。

float t = 0;

void setup() {
  size(600, 600);
  background(255);
}

void draw() {
  background(255);
  stroke(0);

  // 1: 縦線
  float x1 = width/4 + 10 * sin(t);
  line(x1, height/4, x1, 3*height/4);

  // 0: 円
  float diameter = width/4 + 20 * sin(t);
  ellipse(width/2, height/2, diameter, height/2);

  // 8: 2つの重なった円
  float d1 = width/5 + 10 * sin(t);
  float d2 = width/5 + 10 * sin(t + PI);
  ellipse(3*width/4, height/3, d1, d1);
  ellipse(3*width/4, 2*height/3, d2, d2);

  t += 0.03;
}

このコードは、円の大きさと縦線の位置を時間に応じて規則的に変化させます。 t は時間変数であり、フレームごとに増加します。サイン波の振幅や周期を調整することで、アニメーションの動きをカスタマイズできます。

拍動する煩悩をProcessingで描いてみた。正しくはGPT-4に書いてもらった。 pic.twitter.com/4Mf6R7HD7H

— うぱせん (@Rntm0829) March 19, 2023

こんな感じ。