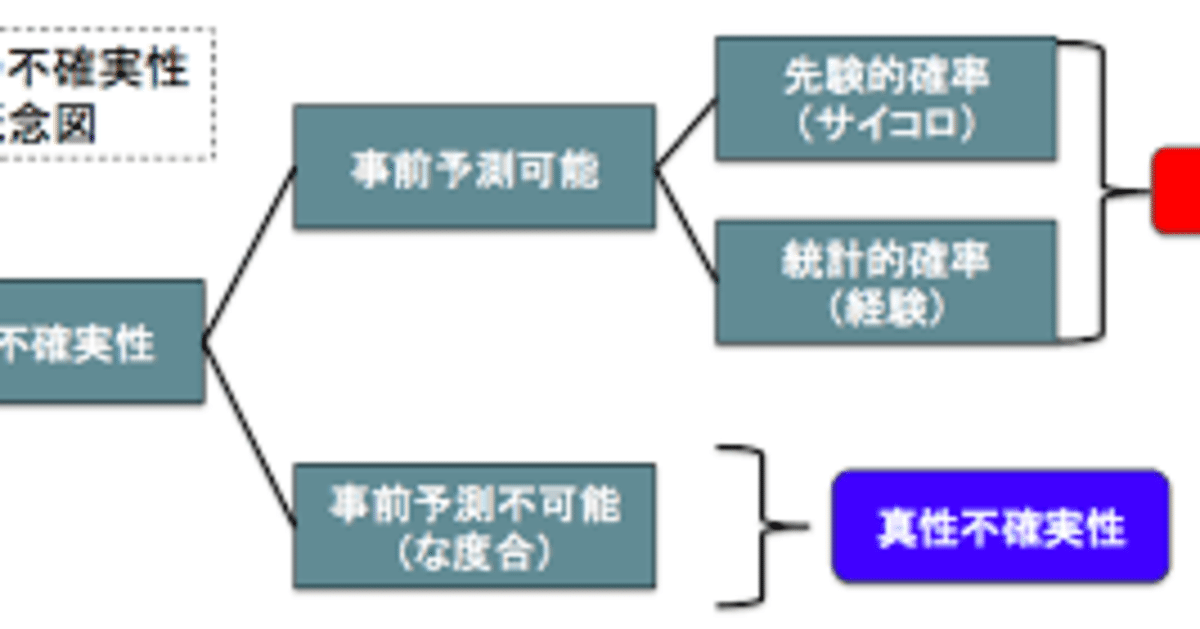
リアルオプションで効果的な投資判断をする方法について

リアルオプション評価は、ＤＣＦ法（ディスカウントキャッシュフロー法）などによる評価と本質的に何が違うのであろうか。
もしある企業が、プロジェクト投資の判断に迷っているとして、DCF法では投資に値しないと結論される投資案件が、リアルオプションによって評価すると投資適格となるとした場合、そこにはいかなる本質が隠されているのであろうか。

筆者は、現在の企業経営において、リアルオプション評価を正規の経営判断に使用しているという例をまだ知らない。しかしながら、リアルオプションの企業経営への適用がある状況下においては本質的な価値を生み、かつ、応用的な活用方法も考えられるのだということをここに記してみようと思う。
（本編には、適宜、追加情報を記載していきます。）

１．金融オプションの理解を深める

証券Ａの現在価格は２千円、１年後のペイオフは確率５０％で４千円、確率５０％で千円。１年後の証券Ａの価格の期待値は、

４０００×０．５＋１０００×０．５　＝　２５００円 (資料では３０００円)

それが、今２千円しているのだから、割引率は

２５００／２０００－１＝２５％　（資料では５０％。いずれも本質的な誤りではない。）

オプションＣは、証券Ａを１年後に３０００円で買うことができるコールオプション。オプションＣの１年後のペイオフは、確率５０％で千円、確率５０％でゼロ。このことからオプションＣの１年後のペイオフの期待値は、

１０００×０．５＋０×０．５＝５００円

オプションＣの価格は、一見、上記の証券Ａの割引率２５％を用いて、

５００／（１＋０．２５）＝４００円

としたくなるが、実はそうではない。そのことを、オプションＣを、証券Ａとリスクフリー債権Ｂ（額面千円）の組み合わせで再現できることで示す。

今、ｍ単位のＡとｎ単位のＢでＣを再現するとしてこのセットをＤとする。ｍ、ｎはマイナスもあり得る。ｍがマイナスとは、ｍ単位の証券Ａを「空売り」することであり、ｍ倍の証券Ａの価格の現金が今手に入り、1年後にその時点の価格のｍ倍を売った先に支払う義務（債務）を保有することになる。ｎがマイナスとは同様にｎ単位のＢの債務を生じることである。

１年後のペイオフを、Ｃと全く同じにするのであるから、確率５０％で、

ｍ×４０００＋ｎ×１１００　＝　１０００

また確率５０％で、

ｍ×１０００＋ｎ×１１００　＝　０

これは二元連立方程式なので、簡単に解けて、

ｍ　＝　（１０００－０）／（４０００－１０００）　＝　１／３
ｎ　＝　－（１０００／３）／１１００＝－０．３０３０３＝－１／３．３

つまり、Ｄは証券Ａを３分の１単位と、債権Ｂをマイナス３．３分の１単位持っている、すなわち３０３円の借金をしている、という組み合わせである。Ｄは１年後のペイオフが全く同じという意味で、オプションＣをひとつ持っているのと同じ。Ｄの価格はＡとＢの価格から簡単に計算できて、

２０００／３　－　１０００／３．３　＝　３６３．６４円

仮にＣの価格がこのＤの価格と異なるのであれば、高いほうを売るのと（空売り）、安い方を買うのとを同時に行うことで確実に価格の差分を儲けることができる。それに市場が気付いた瞬間に高いほうの売りと、安い方への買いが殺到し、価格はあっという間に収束する。つまり、Ｃの価格はＤと同じでなければならない。

以上のことから、オプションの１年後のペイオフの期待値に適用すべき割引率は、証券Ａと同じ２５％ではないことがわかる。
期待値からの割引率は、

（５００／３６３．６４）－１　＝　３７．５％

であり、証券Ａの割引率より高い。すなわち、証券Ａよりリスキーな投資ということになる。

２．リアル・オプションの理解を深める

～～ここから先は有料となりますが、ぜひ最後までお読みいただき、
　　募金活動にご協力ください。この料金で救える命があります～～

プロジェクトＡは、新しい発電設備建設に際し、増設用の土地を購入するかどうかを検討するプロジェクトである。

プロジェクトＡのもたらす収益の現在価値は、２０億円。ただし、発電事業の成否によって、1年後に収益の価値は、５０％の確率で４０億円、５０％の確率で１０％になることが予想されている。増設に必要な建設コストは1年後に２５億円。リスクフリーレートを４％とする時、増設用の土地は、価格がいくらまでであれば購入するべきか。

事前のチェックとして、ＤＣＦ法では、土地は購入されないことを確認しておく。
まず、１年後の収益の期待値は、

４０×０．５　＋　１０×０．５　＝　２５　（億円）

その現在価値が２０億円なので、プロジェクトの割引率は、

（２５／２０）－１　＝　２５％

次に、１年後に２５億円の建設コストの現在価値を求める。１年後の建設コストは確定しているので、１年後に２５億円になるリスクフリー債権を今購入することができ（すなわち、Ａの収益とは異なる割引率で現在価値を求める）、その価格は

２５／（１＋０．０４）＝２４．０４　（億円）

従って、

Ａの収益の現在価値（２０億円）　＜　建設コストの現在価値（２４．０４億円） ＋土地取得費××億円

であるから、ＤＣＦ法で評価すれば、１年後の増設はなく、従って土地を購入することもない。

ここで、暗黙の認識として、「増設用の土地の取引は、今行わないと来年は行えない」という前提を置いていることに気付く。そうでなければ、「１年後に増設の可否を判断して土地を買う」、あるいは、「とりあえず買っておいて、増設しないのであれば売る」ことが可能になり、リアル・オプションで評価をする価値がそもそもなくなってしまう。

つまり、この問題のポイントは、「増設するかしないかは1年後にならないと決められないが、増設に必要な土地は今しか取引できない」という点にある。

これこそがこの問題が「リアル・オプション」であることの本質的なところであって、何がオプションか、というと、

「増設用の土地を購入することは、1年後の増設する『権利』を獲得する、プロジェクトＡを原資産とするオプションである」と考えることができるからである。

すなわち、上記のような暗黙の前提の下では、土地を今購入するかどうかという問題は、このようなオプションを購入するかどうか、という問題と考えることができる、ということに他ならない。

そこでこのリアル・オプションＣをもう少しオプションらしく記述してみると、

（１）行使価格 ２５億円　＝　増設コスト
原資産 Aの価値が２５億円を越えれば（この場合４０億円になれば）権利行使（＝増設）、越えなければ（10億円）行使せず（＝増設しない）。
（２）行使期限 １年後
（３）ペイオフ 確率５０％　ｍａｘ（４０－２５、０）＝１５
確率５０％　ｍａｘ（１０－２５、０）＝０

このように考えれば、あとはこのオプション価格を計算するだけとなる。それは、上記の金融オプションと全く同じように計算できる。
再び、このオプションを、プロジェクトＡとリスクフリー債権Ｂ（額面１０億円）で再現する。ｍ単位のＡと、ｎ単位のＢで構成されるセットＤを考える。Ｄの１年後のペイオフをオプションと全く同一にするのであるから、確率５０％で、

ｍ×４０　＋　ｎ×１．０４　＝　１５

確率５０％で、

ｍ×１０　＋　ｎ×１．０４　＝　０

　二元連立方程式をｍとｎについて解くと、

ｍ　＝　（１５－０）／（４０－１０）　＝　０．５
ｎ　＝　（１５－４０×０．５）／１．０４　＝　－４．８１

　Ｄの価格は、

２０×０．５　－　１０×４．８１　＝　５．１９

従って、オプションＣの価格も５．１９億円ということになる。土地の価格が５．１９億円以下であれば、購入する価値があることになる。

３．リアル･オプションの隠された正体

ここで、もう一度振り返ってリアル・オプションとは何であるか、あるいはリアル・オプション的な考え方に基づいて投資決定をするとはどういうことであるのかをもう一度考えてみたい。

まず、プロジェクトAにおいて、どんな決断が必要であったのかをもう一度吟味してみたい。与えられた状況は次のようなものである。

① １年後に、その時の状況によって、設備を増強するかしないかを決める。
② しかし、増強に必要な土地の取引は今しかできない。
③ １年後の平均的な期待値に基づいて採算を計算すると増強の採算性はない。

　このような状況で、通常は、増設用の土地購入を真剣に検討するだろうか。まず否であろう。特に、③の状況であれば、「二分の一の確率で高い採算が得られる可能性がある」と言っても、初めから検討の対象になどならないであろう。
「リアル・オプションで計算すると買うべきとの結論になります･･･」と言ってみても、そのような結論が採用されるはずがない。

さらに踏み込んで、もう少しそれらしい状況を考えると、③の条件が「採算性有り」の場合はどうであろうか。そういう例ももちろんあり得る。

プロジェクトＡ´：　１年後のプロジェクト価値は、確率５０％で４０億円（Ａと変らず）、確率５０％で２２億円。（悪い方の価値がＡより１２億円高い。）
プロジェクトの割引率を２５％で変えないので、プロジェクトＡ´の現在価値は、２４．８億円。

この場合、

Ａ´の収益の現在価値（２４．８億円）　＞　建設コストの現在価値（２４．０４億円）

であり、Ａの場合とは③の条件が変ってくる。

Ａ´であれば、恐らく検討の対象とはなり、この場合は「土地の購入価格が０．７６億円（＝２４．８－２４．０４）以下であれば、買ってもよい」、という結論が出る可能性がある。

Ａ´をリアル・オプション的に扱えば、土地価格の上限がオプション価格としてＡと同じように計算でき、３．０４億円となる。この違いは何だろうか？リアル・オプションで考えるというのは一体何をしたことになるのだろうか？

それを考えるために、ＡでもＡ´でも増設分の土地価格は３億円であったと仮定して、１年後に何が起こるかに思いを馳せてみる。

まず土地は購入したとしよう。従来法では３億円は０．７６億円を（相当）超えているが、そこはまあ誰かがうまい理屈をひねり出して、会社（経営者）を説得したと考える。

Ａ´の場合、確率５０％でプロジェクト収益の価値は４０億円、確率５０％で２２億円である。２２億円になった場合は、建設コスト２５億円より低いので増設はしない。３億円で１年前に買った土地は「無駄」になって、「購入検討時の見通しが甘かったので、無駄な投資が行われた」という評価が行われることになるだろう。
４０億円の価値がある場合は、４０－２５＝１５億円の利益が見込まれることになり、仮に３億円の土地購入コストを差し引いても充分な利益を確保できることになる。

さて、ここで仮にＡ´と同型のプロジェクトが年間１０個あったとしよう。
確率が５０％ということは、このうち５個のプロジェクトは収益が良く出て増設が行われ、残りの５個は収益が悪く出て購入した土地が無駄になる、ということになる。その結果の全体としての収支は、

（４０－２５－３）×５　＋　（－３）×５　＝　４５億円

サンクコストである土地購入コストを計算に含めるのは理論上は正しくないが、企業の気にする会計上の利益を想定すると、全体としてはこれだけの利益が生じている。
仮に「土地価格が０．７６億円以下なら購入してもよい」というルールを厳密に適用していた場合は、土地購入は行われないので、無駄になる土地も出ないが、収益を上げる機会も失われ、差し引きゼロとなる。つまり、４５億円の利益を上げる機会を喪失したことになる。

気がついてみると、上記の４５億円の計算で、悪い方の収益が２２億円であることは全く関係がない。２２億円でも１０億円でも２５億円の建設コストを下回っていれば増設は行われず購入した土地が無駄になる、というところは全く同じである。
つまり、Ａ´ではなく、プロジェクトＡが１０個年間に発生しても、土地価格が３億円であれば５．１９億円のオプション価格を下回っているので、土地は購入され、１０個のプロジェクト全体では４５億円の収益が生じることとなる。
しかしながら、もし初めに述べた③の条件につまずいて、「こんな投資は箸にも棒にもかからない」と言っていると、この４５億円の利益をみすみす失うこととなる。

この４５億円とはどういう金額かというと、言うまでもないが、設定したオプションの１年後のペイオフの平均的期待値７．５億円から土地価格３億円を引いたものの１０プロジェクト分である。

改めて言い直せば、リアル・オプションの計算は、「個別には３億円を無駄にする覚悟があれば、増設用土地に投資することで平均的には４．５億円の追加利益を上げることができる」と言うことを言っているに過ぎない。
そんなことは、リアル・オプションという小難しい横文字を使わなくても言えるじゃないか、という意見もあろうことと思う。

しかし、リアル・オプションという評価手法を使うかどうかは別として、これらプロジェクト投資の判断に迷っている会社が、仮に「個別の損（リスク）を覚悟しつつ、全体として投資リターンを高めていく方法論」を持っていないとしたならば、リアルオプションという評価方法も価値を生むのではないかと考える。

このような考え方を投資評価の方法論として定着させるには、次の二点について充分な理解が得られなければならない。

（１） 個別には損をしなければ、投資活動から平均的に高い利潤を得ることはできない。
（２） Ａ´だけではなく、一見すると「箸にも棒にもかからない」、Ａにも投資できる仕組みがなければならない。

（１）は、もともとリアル・オプション理論が創出された背景とも関係する。１９８０年代の米国では、投資決定方法論としてＤＣＦ法が定着してきたが、実態に合わないことが指摘されていた。何よりも、日本企業の積極的な投資戦略の前に、米国企業は次々と敗退していたからである。日本企業のような積極的な投資を正当化し、高い成長率を実現する投資方法論は何なのか。リアル・オプションの生まれた背景にはこのような米国企業の深刻な問題意識があったのではないだろうか。

企業経営者からは、「失敗を怖れるな」、「果敢にチャレンジしろ」などの言葉が出るが、一方では、個別のプロジェクトの採算を事前、事後で厳しく評価する仕組みはますます厳密に適用されるようになっているのが今の日本企業（特に大企業）の実態であるように感じる。

言うまでもないが、プロジェクトは生き物であり、事前の工夫や、実行後の不断の努力で少しでも投資リターンを高める努力がなされるべきである。すなわち、継続的な評価とその結果に基づく行動の修正、いわゆるＰＤＣＡサイクルを回す必要がある。

しかし、私たちが投資を考える時、「事前に採算を充分吟味した上で選択し、実行に当たってＰＤＣＡをきちんと回せば、本来損はしないはず」と暗黙の内に思い込んではいないだろうか。そして、そのような思い込みが、現在の投資評価の枠組みを保持している根源ではないのだろうか。

リアル・オプション理論は、「そのような思い込みは投資不足＝リターン不足を招く」と教えている。つまり、ＤＣＦ法の意味で儲かることがわかっているプロジェクトだけに投資をしているのでは、損はしないかもしれないが、株主から預かった資本の利潤を最大限に追求していることにはならない、ということになるのである。
現代の株主は、会社が損をしないことでは満足せず、最大限の利益を上げ、最大限の成長を遂げることを要求しており、象徴的な言い方になるが、ＤＣＦ法ではその期待に応えきれない。

「虎穴にいらずんば虎子を得ず」という諺があるが、これは「虎穴に入ってもうまくやれば怪我をせずに虎子を得られる」ということではなく、「虎穴に入って命を落とす人が出ないと、虎子は得られない」という意味に解釈するべきであろう。

もしそうであるならば、これは単にプロジェクト評価の方法論だけの問題ではない。投資プロジェクトを動かすのは人であり、虎穴に入って命を落とす人をどうするのか、という点まで含めて仕組みを作らなければ虎子を得るプロジェクトを次々に生み出すことはできない。サントリーの佐治敬三は、「やってみなはれ」で有名であるが、同時に「『やってみなはれ』一発ではいかんので、やってみた結果については、俺が骨をひろってやるぞと」語っていたという。

さらに言えば、これは単にプロジェクトに関わる人のモチベーションやインセンティブの問題でもない。人は人財であって、持てる人財と、プロジェクトの最も効果的なマッチングから最大限の成果を上げるのは、すぐれて組織マネジメントの問題である。
優秀な人財ほど、どのプロジェクトでも力を発揮する能力を持っている。しかし、その人財をある特定のプロジェクトに配置すれば、そのプロジェクトの成功確率は上がるかもしれないが、一方で、他のプロジェクトを任せることはできなくなる。
どこかの虎穴で命を落とす可能性も踏まえつつ、どの人財をどのプロジェクトに配置するのか？それを考える手法を私たちは持たなければならないであろう。

リアル・オプションがそのような方法論の最善のものなのかどうかはわからない。ひとつの方法論ではあるが、ＤＣＦ法の限界が露呈したのと同様、リアル・オプションもいろいろ批判をされる可能性があるだろう。
しかし、ＤＣＦ法だけに頼っていては見えてこない収益機会を発見する手がかりとなる、という意味では意味があると思われる。

その観点で印象的なのが、上記（２）で述べた通り、ＤＣＦ法的発想では「箸にも棒にもかからない」プロジェクトＡが、Ａ´同様に、リアル・オプションでは投資対象になるという例であろう。

リアル・オプションはさまざまなケースに適用可能である。決定を遅らせることの価値、工場の操業の継続・停止、操業規模の拡大・縮小などについて、単純にキャッシュフローを推定するだけでは見えてこない経済性を見せてくれる。リアル・オプションのもたらす結論は、しばしば直感的には納得できるものである。しかし、ＤＣＦ的な方法論ではなかなか正当化できない。直感を鍛え、それに理論的根拠を与える手法としてリアル・オプションを活用する意義はあるように思う。

繰り返しになるが、市場は高い投資リターンを求めており、その期待に応えようとすれば、一見損なプロジェクトにも投資することが求められる、というのが（２）から得られる教訓である。

４． 最大限の投資リターンを求めて

前述したのは、「リアル・オプションという手法が問題なのではなく、投資リターンが構造的に低く抑えられてしまうことが問題なのだ」ということである。

もし、この問題意識が正しいとするならば、本来追及すべきなのは、「リアル・オプションをどう使うか」である前に、「あなたの企業は最大限の投資リターンを上げているか？」という検証となるだろう。

これらの検証を通じて「リターン不足」が現実の問題として認識されてはじめて、リアル・オプションの有効性を真剣に議論できる素地が形成されていくのだと思う。