
【高校数学】n進法を攻略する
皆さんこんにちは!
日常の中で様々なことに疑問を持ち、学んでいっているのですが、せっかくなのでそれを発信していき、共有していこうと思っている、そんな企画でございます。
今回のテーマは「n進法」
厄介な計算についてご紹介していきます。
n進法
n進法とは、「nで位が上がる法則」です。
具体例で何となく理解してください。
一般的なもの・・・10進法
9の次は1桁上がって10
99の次は1桁上がって100
時計・・・60進法
59秒の次は1桁上がって1分
59分の次は1桁上がって1時間
コンピューター・・・2進法
1の次は1桁上がって10
11の次は1桁上がって100
一般的に我々人間の指は合計10本であり、"10"という数字はなじみ深く、そのため人間の間では10進法が発展してきたと言われています。
一方、コンピューター星人の世界では電気信号が流れるor流れないですべてが決まります。
流れる方を1,流れない方を0とすると、この世界には1と0しか存在しないことになります。
コンピューター星人はこの二つの数字だけで生活しなくてはいけないので、非常に不便な人生(コンピューター生?)を送らなくてはいけなさそうです・・・("二"つという概念も存在しないのでうまく説明できなくなりますね)
かといって、60進法もなかなか面倒くさそうです。
お饅頭を何個かまとめて箱詰めして売るとき、10個って非常にキリがいいですけど、60進法の世界ではキリがいい数字って60です。(多分)
60個入りの饅頭とかまぁまぁな量ですよね。
お土産で買うにしてもなかなか中途半端そう・・・
古代メソポタミアでは大真面目に60進法が適用されていたのですから驚きです。(その時の名残で時間は未だに60進法です。これに関してはもう慣れてしまいましたね)
ちなみに60進法が使われていた理由には、約数がめちゃくちゃ多くて
「○分の一時間」みたいな言い方がいろいろできるからってのがあるみたいです。
確かに5分も、10分も、15分も、20分も、30分も何となくキリのいい時間って感じがします。
他にも16進法とか12進法とか7進法とかいくらでも作り出すことができますが、まぁ10進法が一番使い心地よさそうです。
人間に生まれてよかった~
桁の抽象化
このまま我々は他進法を用いる生物と意思を疎通することはできないのか・・・
相手が何進法を使っていようが、同じように"計算"できなくてはいけません。
その計算方法を考えに考えに考えました・・・
抽象化、一般化というのは数学で行われるかなり基本的な考えです。
皆さんは「1+1とか2+3とか限られた数だけしか足し算できない!」なんてことないですよね?
それが45+82でも123+456でもx+yでも計算できるのです。
どんな足し算でも計算できる(一般的な足し算を計算できる)のです。
この考えをn進法でも使います。
10進法以外のどんな進法でも計算できるようにするのです。
「こんなの勉強して何に使うんだ・・・」シリーズでも結構上位にいるこのn進法ですが、コンピューターの気持ちを理解しようってわけなんですね。
非常に国際的ですね!!
そのためにはまず、「桁とは何か」を考えなくてはなりません。
何となく「桁」と使っていますが、もう少し具体的に抽象化していきましょう。(矛盾)
よんでみよう!
読んでみてください。
24・・・「にじゅうよん」
365・・・「さんびゃくろくじゅうご」
2桁目の数は、その数に「じゅう」を付け加えて発音します。
3桁目の数は、「ひゃく」を付け加えます。
これはどういうことかというと、
10が2個あるという意味です。
なので、24は
「10が2個、1が4個」
365は
「100が3個、10が6個、1が5個」
と言い換えることができるわけですね。
10進法なので10個の束にして、それが10個集まったら次の桁に移行していることが分かると思います。
(10が10個あったら、それは「じゅうじゅう」と呼ばずに「ひゃく」と呼びます)
そして更にn進法を理解するために、10とか100を指数で表してみましょう。
![]()
この調子で1とか1000とか10000も指数表記にしてみると・・・
![]()
これを見てお気づきかもしれませんが、10の肩に乗ってる数字+1がその時の桁数になるのです!なので、
![]()
は3桁の数字だということが分かりますね。
いやまぁ、かなり当たり前のことなのですが・・・
しかし、この「○乗という形で考える」というのがn進法を一般化するのにとても重要なのです!
2進法を見ていきましょう!
2進法の桁数
10進法は10で桁が変わるので、10の○乗で考えました。
では、2進法だったらどうなるでしょうか?
・10進法と同じように2の○乗で桁が変わる
・2の肩に乗ってる数字+1がその時の桁数
ってルールにしてみると・・・
![]()
こんな感じになりませんかね?
てことはつまり、
2進数の世界では10が2を表し、100が4を表しているということなんです。
なので、例えば「10011」という数字は、
5桁目が1、4桁目が0、3桁目が0、2桁目が1、1桁目が1なので

ということで、10進法で表すと19だということが分かりました。
なんと!
2進法の世界の数字が解読できたのです!!おめでとう!!ありがとう!!
他進法に応用
10進法も2進法も桁が上がるときの数字の○乗という部分か重要だったことになります。
てことは、このルールを使ってやれば他の進法も解読できることになりそうです。
例)16進法
16の○乗で桁が変わります。

例)60進法
60の○乗で桁が変わります。

こんな感じでやっていけば何進法でも10進法の我々が普段見慣れている形に書き直すことができます。
みなさんもn進法星人と出会ったときにはぜひ使ってみてください!!
めざせ翻訳家!
さて、今まではn進法星人が何を言っているのかを理解するための方法を考えてきました。
英語で言うところの「読む」とか「聞く」ですね。
しかしそれだけではコミュニケーションは成立しません。
n進法星人に我々の考えを伝えなくてはならないのです。
「書けるよう」に「話せるよう」になりましょう!
2進法を10進法に戻す
では、19を2進法星人に説明することにします。
こいつらは0と1しか見ないで生活してきたので2より大きい数字は分かりません。非常に不便な生活を送っていますよね。
要するに、2の倍数は全て分からないのです。
仕方ないのでどんどん2で割っていって、2という数字を消してあげましょう。

何で⇒の式が出てくるのかというと、
割り算っていうのはそういう意味だからです。
深く考えないで「そういうもんだ」と思ってください。
勘のいいガキは好きではありません。
あまりっていうのは半端な部分で、
その半端な部分を足してあげれば元のものに戻りますよね。
次に、先ほどの式をどんどんいじっていきましょう。
![]()
この式の9に
![]()
を代入
![]()
右辺を展開します。

今度は4に
![]()
を代入してみます。

はい。
その後も続けて計算してしまいました。
こんな感じになりますよね。
で、最後の一行を少し書き換えてやると・・・

となり、
これはまるっきし2進法の形であることが分かります。
つまり、19=10011ということですね。
先ほど10011を10進法に戻しましたが、再び2進法に戻すことができました。
10進法をn進法に戻したいときは
nで最後まで割っていき、その時出たあまりの数を対応する桁に埋め込めばよい
ということが分かったと思います。
ちょっと他の進数で例題を見てみましょうか。
例)3281を16進数で

例)10285秒を分かりやすく

この、時間の例を見てみると、
「60で割ってあまりを・・・」みたいな計算を普段からやっていることに気づくと思います。
小数を定義する
さて、ここまで一般的なn進法を考えてくると、なんとn進法の小数までわかるようになるのです。
1.58とかいう数字を2進法で表すって実は結構難しいんですよね。
「1の次が10、11の次が100・・・」ってことしかわかってないと、
「え?0.2が0.10?あれ?0.1も0.10だよな・・・?」と、訳の分からんことになってしまいます。
では、手始めに10進法の小数を考え直してみましょう。
そもそも小数ってなんやねん
10進法の桁は
![]()
ということが先ほど分かりました。
ってことは、nがどんどん減っていく方向も考えられるのです。

こんな感じですね。
実際に、

であることが分かると思います。
てことはつまり、
![]()
ということなんですよね。
なるほどなるほど。
2進法で書かれた小数を読む
では、この理論を2進法にも当てはめてみましょう。
すると・・・

このようなことが言えますね。
では、実際に2進法の小数を読んでみるとしましょう。
例)110.01

こんな感じで10進法に直すことができますね。
同じやり方をすれば16進法とか7進法とか12進法とか全てに応用できるはずですが、小数の指数は小数点以下がめっちゃ細かくなって面倒くさそうなので今回はやらないです。
やる気のある人はやってみてください。
10進法で書かれた小数を2進法で書く
今度は10進法の小数を2進法に変えてみましょう!
例)6.25
↑でやった例なので、答えは分かっていると思います。
実際にその数字になるかチェックしてみましょう。
まず、6=110なので整数部分はオッケー。残りの0.25が何なのかを考えればいいだけです。
そのためには0.25を分数で書き表すことから始めます。

こう書くことができるので、0.01だという言うことが判明しました。
先ほどの110と合わせて、
110.01
が答えになるわけです。
見事元に戻りました!
今回、0.25という結構わかりやすい数字だったのですが、
複雑な数になるともう少しコツがいります。
例)0.101(2進数)
まずはこの2進数を10進数にしてみましょう。

はい。
0.625らしいです。
では、再び2進法に戻してみましょう。
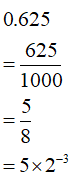
こんな感じになるのですが、
ここで気を付けてほしいことがあって、
「5」という数字は2進法の世界の人間は理解できなかったはずですよね?
なので、2進法に直す時に5を使ってはいけないのです。
では、どうするのかというと、
5を2進法で表記して、101にします。
そして、それを小数点第三位までずらせばいいのですね。
つまり、
0.101
となるわけです。
お!無事元に戻りましたね!
同様の方法で10進法の小数を16進法とか60進法とかに直すこともできます。
もちろん、面倒くさいのでやりませんが!
おしまい
いかがだったでしょうか?
普段使いなれない数字なのでややこしくて結構疲れたと思います。
僕も何度も見直して理解していきました。
もうわけわかめ
多分コンピュータを扱っている人はいつもこの計算をやってるんだと思いますよ。
凄いですねぇ
ということで今回はここまで。
今回の記事がためになったという方、面白かったという方はぜひSNS等でシェアしてくださると嬉しいです。
間違いがあったりしたらコメント等で教えてください。
また、「お疲れ!コーヒーでも飲みな!」という方はサポートをしてくださるととても励みになります!
また、他の記事もぜひ見てみて、ついでにTwitterのフォローもお願いします!!⇒https://twitter.com/mazenemaze
それでは、また次回の記事でお会いしましょう!!
