高校数学をプログラミングで解く（数学A編）「2-9 2つの円の位置関係」

割引あり

MK's papa

2023年9月6日 06:30

マガジンリスト　＞　数学A編 2.図形の性質　＞　2-9 2つの円の位置関係

はじめに

今回は、数学Aで学ぶ「2つの円の位置関係」について、２つの円の位置関係を分類し、その位置関係に応じて共通接線を描くプログラムを作成します。

2つの円の位置関係を分類する

まず、2つの円の位置関係についてまとめておきます。

２つの円の位置関係
2つの円$${\mathrm{O}}$$と$${\mathrm{O}'}$$の半径をそれぞれ$${r}$$と$${r'}$$（ただし、$${r>r'}$$）とおきます。また、2つの円の中心間の距離を$${d}$$とします。このとき、

I. $${d>r+r'}$$の場合、2つの円は互いに外部にあり、共通接線を4本もつ。
II. $${d=r+r'}$$の場合、2つの円は外接し、共通接線を３本もつ。
III. $${r-r' < d < r+r' }$$の場合、２つの円は２点で交わり、共通接線を２本もつ。
IV. $${d=r-r' }$$の場合、２つの円は内接し、共通接線を１本もつ。
V. $${d < r-r' }$$の場合、一方の円が他方の円の内部にあり、共通接線をもたない。

２つの円の位置関係を分類するプログラム

では、2つの円の位置関係を分類して、その結果をコンソールに出力するプログラムを作成します。そのために、大きい円$${\mathrm{O}}$$の半径を$${r=150}$$（プログラムでは変数名をr1としています）、小さい円$${\mathrm{O}'}$$の半径$${r'=100}$$（プログラムでは変数名をr2としています）とします。

// 2つの円の位置関係
void setup(){

  // 円Oと円O'との距離d
  float d;
  d = 300.0;
  // 円Oの半径r1
  float r1;
  r1 = 150.0;
  // 円O'の半径r2（ただし、r2 < r1)
  float r2;
  r2 = 100.0;
    
  if( d > r1+r2 ){
    println("互いに外部にある 共通接線は4本");
  } else if( d == r1+r2 ){
    println("外接する 共通接線は3本");
  } else if( d > r1-r2 && d < r1+r2 ){
    println("2点で交わる 共通接線は2本");
  } else if( d == r1-r2 ){
    println("内接する 共通接線は1本");
  } else {
    println("一方が他方の内部にある 共通接線はなし");
  }
}

ソースコード1　２つの円の位置関係を判別するプログラム

ソースコード1を、Processingの開発環境ウィンドウを開いて（スケッチ名を「position_of_two_circles_discriminant」としています）、テキストエディタ部分に書いて実行すると、図1のように分類結果がコンソールに出力されます。

ソースコード1では、2つの円の中心間の距離を$${d=300}$$としていますので、$${d>r+r'}$$となり、分類結果として「互いに外部にある　共通接線は４本」がコンソールに出力されています。
2つの円の中心間の距離$${d}$$の値を変えて実行してみると、コンソールに出力される結果が変わります。たとえば、$${d=250, 125, 50, 25}$$のように値を変えて実行して正しい分類結果がコンソールに出力されるか、試してみてください。

共通接線を描く

次に、2つの円の位置関係の分類結果に合わせて、2つの円と共通接線を描くプログラムを作成していきます。

接線を描くための準備（座標軸の設定）

図2のように座標軸を設定します。円$${\mathrm{O}}$$の中心座標を$${(0,0)}$$、円$${\mathrm{O}'}$$の中心座標を$${(d,0)}$$とおきます。

以下で、この座標軸を基準にして２つの円の位置関係を考慮した共通接線を描くための準備を進めていきます。

2つの円を描くプログラム

接線を描く前に、２つの円を描くプログラムを準備します。ソースコード1に2つの円を描くプログラムに追加します。

// 2つの円の位置関係
void setup(){
  size(1000, 500); // キャンバスの大きさを指定する
  translate(width/2.0, height/2.0); // 座標の中心をキャンバスの中心に移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する
  background(255,255,255); // 背景を白色にする
  noFill(); // 図形の塗りつぶしなし
  noLoop(); // 繰り返し処理をしない
  
  // 円Oと円O'との距離d
  float d;
  d = 300.0;
  // 円Oの半径r1
  float r1;
  r1 = 150.0;
  // 円O'の半径r2（ただし、r2 < r1)
  float r2;
  r2 = 100.0;
  
  // 円Oの中心位置
  float O1_x, O1_y;
  O1_x = 0.0;
  O1_y = 0.0;
  // 円O'の中心位置
  float O2_x, O2_y;
  O2_x = d;
  O2_y = 0.0;

  // 円Oと円O'を描く
  circle(O1_x, O1_y, 2.0*r1);
  circle(O2_x, O2_y, 2.0*r2);
  point(O1_x, O1_y);
  point(O2_x, O2_y);
    
  if( d > r1+r2 ){
    println("互いに外部にある 共通接線は4本");
  } else if( d == r1+r2 ){
    println("外接する 共通接線は3本");
  } else if( d > r1-r2 && d < r1+r2 ){
    println("2点で交わる 共通接線は2本");
  } else if( d == r1-r2 ){
    println("内接する 共通接線は1本");
  } else {
    println("一方が他方の内部にある 共通接線はなし");
  }
}

ソースコード2　2つの円を描くプログラム

ソースコード2を、Processingの開発環境ウィンドウを開いて（スケッチ名を「position_of_two_circles」としています）、テキストエディタ部分に書いて実行すると、実行ウィンドウのキャンバスに２つの円が描かれます。

以下で、２つの円に対してそれらの位置関係に合わせて共通接線を描くためのアルゴリズム設計を行い、プログラムを作成していきます。

2つの円が互いに外部にあるときの共通接線

2つの円が互いに外部にあるときの共通接線は図4のように４本あります。

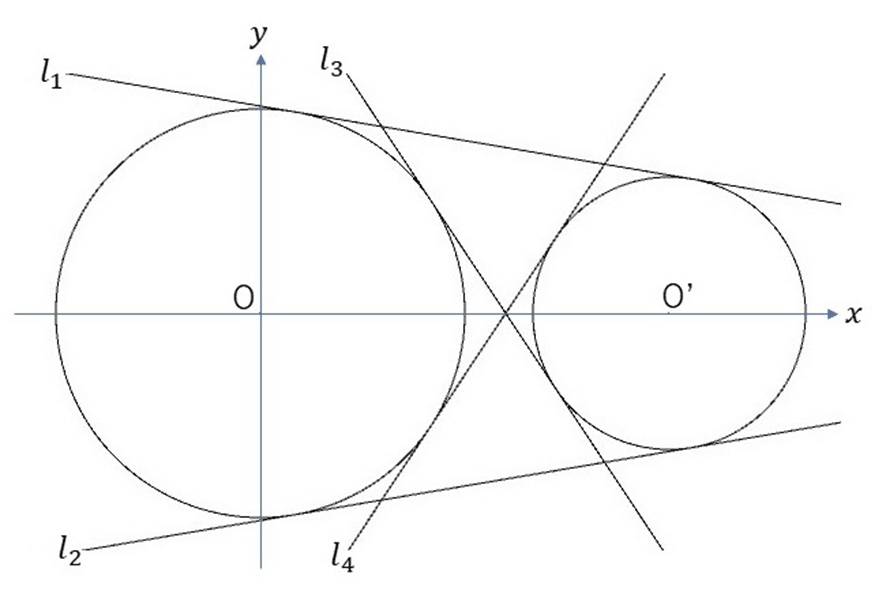
これらの接線の描き方を以下で考えていきます。

接線$${l_1, l_2}$$
接線$${l_1}$$を描くために、接線$${l_1}$$の方程式を考えます。
図5のように、接線$${l_1}$$と円$${\mathrm{O}}$$および$${\mathrm{O}'}$$との接点をそれぞれ$${\mathrm{T_1}}$$および$${\mathrm{T_1'}}$$とします。また、接線$${l_1}$$と$${x}$$軸との交点を$${\mathrm{P}}$$とし、点$${\mathrm{T_1}}$$から$${x}$$軸に下した垂線との交点を$${\mathrm{Q}}$$とします。
接線$${l_1}$$は点$${\mathrm{T_1}}$$を通り、直線$${\mathrm{OT_1}}$$に垂直な直線となるので、接点$${\mathrm{T_1}}$$の座標$${(x_1, y_1)}$$が分かれば、接線$${l_1}$$の方程式は

$$
y=m_1x+n_1, \ m_1=-\frac{x_1}{y_1}, \ n_1=\frac{r^2}{y_1}
$$

と求めることができます。

そこで、点$${\mathrm{T_1}}$$の座標$${(x_1, y_1)}$$を求めていきます。この導出は比較的簡単です。
△$${\mathrm{POT_1}}$$と△$${\mathrm{PO'T_1'}}$$は互いに相似の関係になっているので、

$$
\mathrm{OP}=\frac{r}{r-r'} d, \ \mathrm{PT_1}=\frac{r}{r-r'} \sqrt{d^2-(r-r')^2}
$$

となります。また、$${\triangle \mathrm{POT_1}}$$と$${\triangle \mathrm{T_1OQ}}$$は互いに相似の関係になっているので、

$$
x_1=\mathrm{OQ}=\frac{r}{d}(r-r'), \ y_1=\mathrm{QT_1}=\frac{r}{d} \sqrt{d^2-(r-r')^2}
$$

となります。
接線$${l_2}$$は接線$${l_1}$$を$${x}$$軸に対して線対称に描いたものになるので、接線$${l_2}$$の方程式は

$$
y=m_2x+n_2, \ m_2=\frac{x_1}{y_1}, \ n_2=-\frac{r^2}{y_1}
$$

となります。

接線$${l_3, l_4}$$
接線$${l_3}$$を描くために、接線$${l_3}$$の方程式を考えます。
図6のように、接線$${l_3}$$と円$${\mathrm{O}}$$および$${\mathrm{O}'}$$との接点をそれぞれ$${\mathrm{T_3}}$$および$${\mathrm{T_3'}}$$とします。また、接線$${l_3}$$と$${x}$$軸との交点を$${\mathrm{P}}$$とし、点$${\mathrm{T_3}}$$から$${x}$$軸に下した垂線との交点を$${\mathrm{Q}}$$とします。
接線$${l_3}$$は点$${\mathrm{T_3}}$$を通り、直線$${\mathrm{OT_3}}$$に垂直な直線となるので、接点$${\mathrm{T_3}}$$の座標$${(x_3, y_3)}$$が分かれば、接線$${l_3}$$の方程式は

$$
y=m_3x+n_3, \ m_3=-\frac{x_3}{y_3}, \ n_3=\frac{r^2}{y_3}
$$

と求めることができます。

そこで、$${\mathrm{T_3}}$$の座標$${(x_3, y_3)}$$を求めていきます。
$${\triangle \mathrm{POT_3}}$$と$${\triangle \mathrm{PO'T_3'}}$$は互いに相似の関係になっているので、

$$
\mathrm{OP}=\frac{r}{r+r'} d, \ \mathrm{PT_3}=\frac{r}{r+r'} \sqrt{d^2-(r+r')^2}
$$

となります。また、$${\triangle \mathrm{POT_3}}$$と$${\triangle \mathrm{T_3OQ}}$$は互いに相似の関係になっているので、

$$
x_3=\mathrm{OQ}=\frac{r}{d}(r+r'), \ y_3=\mathrm{QT_3}=\frac{r}{d} \sqrt{d^2-(r+r')^2}
$$

となります。
接線$${l_4}$$は接線$${l_3}$$を$${x}$$軸に対して線対称に描いたものになるので、接線$${l_4}$$の方程式は

$$
y=m_4x+n_4, \ m_4=\frac{x_3}{y_3}, \ n_4=-\frac{r^2}{y_3}
$$

となります。

4つの共通接線を描くプログラム
４つの共通接線の方程式が得られたので、これらの接線を描くためのプログラムを作成します。ソースコード2の

  if( d > r1+r2 ){
    println("互いに外部にある 共通接線は4本");

と

  }else if( d == r1+r2 ){

との間に下記のコードを追加します。

    // 点T1の座標
    float T1_x, T1_y;
    T1_x = (r1-r2) / d * r1;
    T1_y = sqrt( d*d - (r1-r2)*(r1-r2) ) / d * r1;
    // 直線l1の傾きと切片
    float m1, n1;
    m1 = -T1_x / T1_y;
    n1 = r1*r1 / T1_y;
    
    // 点T2の座標
    float T2_x, T2_y;
    T2_x = (r1-r2) / d * r1;
    T2_y = -sqrt( d*d - (r1-r2)*(r1-r2) ) / d * r1;
    // 直線l2の傾きと切片
    float m2, n2;
    m2 = -T2_x / T2_y;
    n2 = r1*r1 / T2_y;

    // 点T3の座標
    float T3_x, T3_y;
    T3_x = (r1+r2) / d * r1;
    T3_y = sqrt( d*d - (r1+r2)*(r1+r2) ) / d * r1;
    // 直線l3の傾きと切片
    float m3, n3;
    m3 = -T3_x / T3_y;
    n3 = r1*r1 / T3_y;
    
    // 点T4の座標
    float T4_x, T4_y;
    T4_x = (r1+r2) / d * r1;
    T4_y = -sqrt( d*d - (r1+r2)*(r1+r2) ) / d * r1;
    // 直線l4の傾きと切片
    float m4, n4;
    m4 = -T4_x / T4_y;
    n4 = r1*r1 / T4_y;
    
    line(-width/2.0, m1*(-width/2.0)+n1, width/2.0, m1*(width/2.0)+n1); // l1
    line(-width/2.0, m2*(-width/2.0)+n2, width/2.0, m2*(width/2.0)+n2); // l2
    line(-width/2.0, m3*(-width/2.0)+n3, width/2.0, m3*(width/2.0)+n3); // l3
    line(-width/2.0, m4*(-width/2.0)+n4, width/2.0, m4*(width/2.0)+n4); // l4

ソースコード3　４つの接線を描くプログラム（ソースコード2に追加）

ソースコード3を追加して、スケッチ「position_of_two_circles」を実行すると、図7のように互いに外部にある２つの円に対して４つの共通接線を描きます。

2つの円が外接するときの共通接線

2つの円が外接するときの共通接線は図8のように3本あります。

これらの接線の描き方を以下で考えていきます。

接線$${l_1, l_2}$$
接線$${l_1}$$及び$${l_2}$$の方程式は上記「2つの円が互いに外部にあるときの共通接線」の節で導出した$${l_1}$$と$${l_2}$$の方程式と同じものになりますので、導出方法はそちらをご覧ください。

接線$${l_3}$$
接線$${l_3}$$は$${y}$$軸と並行で2つの円の接点$${(r,0)}$$を通る直線なので、接線$${l_3}$$の方程式は、

$$
x=r
$$

となります。

3つの共通接線を描くプログラム
3つの共通接線の方程式が得られたので、これらの接線を描くためのプログラムを作ります。ソースコード2の

  } else if( d == r1+r2 ){
    println("外接する 共通接線は3本");

と

  } else if( d > r1-r2 && d < r1+r2 ){

との間に下記のコードを追加します。

    // 点T1の座標
    float T1_x, T1_y;
    T1_x = (r1-r2) / d * r1;
    T1_y = sqrt( d*d - (r1-r2)*(r1-r2) ) / d * r1;
    // 直線l1の傾きと切片
    float m1, n1;
    m1 = -T1_x / T1_y;
    n1 = r1*r1 / T1_y;
    
    // 点T2の座標
    float T2_x, T2_y;
    T2_x = (r1-r2) / d * r1;
    T2_y = -sqrt( d*d - (r1-r2)*(r1-r2) ) / d * r1;
    // 直線l2の傾きと切片
    float m2, n2;
    m2 = -T2_x / T2_y;
    n2 = r1*r1 / T2_y;

    line(-width/2.0, m1*(-width/2.0)+n1, width/2.0, m1*(width/2.0)+n1); // l1
    line(-width/2.0, m2*(-width/2.0)+n2, width/2.0, m2*(width/2.0)+n2); // l2
    line(r1, -height/2.0, r1, height/2.0); // l3

ソースコード4　3つの接線を描くプログラム（ソースコード2に追加）

ソースコード4を追加し、円$${\mathrm{O}}$$と円$${\mathrm{O}'}$$との距離$${d}$$の値を

  // 円Oと円O'との距離d
  float d;
  d = 250.0;

に変更して、スケッチ「position_of_two_circles」を実行すると、図9のように外接する２つの円に対して3つの共通接線を描きます。

2つの円が2点で交わるときの共通接線

2つの円が２点で交わるときの共通接線は図10のように2本あります。

これらの接線の描き方を以下で考えていきます。

2つの共通接線を描くプログラム
2つの共通接線の方程式が得られたので、これらの接線を描くためのプログラムを作ります。ソースコード2の

  } else if( d > r1-r2 && d < r1+r2 ){
    println("2点で交わる 共通接線は2本");

と

  } else if( d == r1-r2 ){

との間に下記のコードを追加します。

    // 点T1の座標
    float T1_x, T1_y;
    T1_x = (r1-r2) / d * r1;
    T1_y = sqrt( d*d - (r1-r2)*(r1-r2) ) / d * r1;
    // 直線l1の傾きと切片
    float m1, n1;
    m1 = -T1_x / T1_y;
    n1 = r1*r1 / T1_y;
    
    // 点T2の座標
    float T2_x, T2_y;
    T2_x = (r1-r2) / d * r1;
    T2_y = -sqrt( d*d - (r1-r2)*(r1-r2) ) / d * r1;
    // 直線l2の傾きと切片
    float m2, n2;
    m2 = -T2_x / T2_y;
    n2 = r1*r1 / T2_y;

    line(-width/2.0, m1*(-width/2.0)+n1, width/2.0, m1*(width/2.0)+n1); // l1
    line(-width/2.0, m2*(-width/2.0)+n2, width/2.0, m2*(width/2.0)+n2); // l2

ソースコード5　2つの接線を描くプログラム（ソースコード2に追加）

ソースコード5を追加し、円$${\mathrm{O}}$$と円$${\mathrm{O}'}$$との距離$${d}$$の値を

  // 円Oと円O'との距離d
  float d;
  d = 125.0;

に変更して、スケッチ「position_of_two_circles」を実行すると、図11のように2点で交わる２つの円に対して2つの共通接線を描きます。

2つの円が内接するときの共通接線

2つの円が内接するときの共通接線は図12のように1本あります。

これらの接線の描き方を以下で考えていきます。

接線$${l_1}$$
接線$${l_1}$$は$${y}$$軸と並行で2つの円の接点$${(r,0)}$$を通る直線なので、接線$${l_1}$$の方程式は、

$$
x=r
$$

となります。

1つの共通接線を描くプログラム
1つの共通接線の方程式が得られたので、これらの接線を描くためのプログラムを作ります。ソースコード2の

  } else if( d == r1-r2 ){
    println("内接する 共通接線は1本");

と

  } else {

との間に下記のコードを追加します。

    line(r1, -height/2.0, r1, height/2.0); // l1

ソースコード6　1つの接線を描くプログラム（ソースコード2に追加）

ソースコード6を追加し、円$${\mathrm{O}}$$と円$${\mathrm{O}'}$$との距離$${d}$$の値を

  // 円Oと円O'との距離d
  float d;
  d = 50.0;

に変更して、スケッチ「position_of_two_circles」を実行すると、図13のように内接する２つの円に対して1つの共通接線を描きます。

一方の円が他方の円の内部にあるときの共通接線

一方の円が他方の円の内部にあるとき共通接線は図14のように存在しません。

共通接線がないので、ソースコードへの追記することはないですが、ソースコード 1の円$${\mathrm{O}}$$と円$${\mathrm{O}'}$$との距離$${d}$$の値を

  // 円Oと円O'との距離d
  float d;
  d = 25.0;

に変更して、スケッチ「position_of_two_circles」を実行すると、図15のように一方の円が他方の円の内部にある図形を描きます。

まとめ

今回は、数学Aで学ぶ「２つの円の位置関係」について、２つの円の位置関係を分類し、その位置関係に応じて共通接線を描くプログラムを作成しました。ポイントは２つの円の中心を$${x}$$軸上に置いたことです。これにより、接線の方程式の導出がやりやすくなったと思います。一般にプログラムで図形を描く場合、座標軸をうまくとると必要な点の座標位置や直線の方程式などの導出がしやすくなります。座標軸の設定の仕方についてすこしずつ慣れていってください。

参考文献

改訂版教科書傍用スタンダード数学A（数研出版、ISBN9784410209277）

演習問題

図8に対して、円$${\mathrm{O}'}$$に外接し、かつ接線$${l_1, l_2}$$に接する円$${\mathrm{O}_3}$$を赤色で描くプログラムを作成してください。

演習問題の解答例

ここから先は

468字 / 1画像 / 1ファイル

ログイン

この記事が気に入ったらチップで応援してみませんか？