見出し画像

高校数学をプログラミングで解く（数学A編）「1-5 事象と確率」

割引あり
MK's papa

マガジンリスト　＞　数学A編 1.場合の数と確率　＞　1-5 事象と確率


はじめに

今回は、数学Aで学ぶ「事象と確率」について、いくつかの確率を計算するプログラムを作成します。

事象と確率、確率の基本性質

まず、事象と確率、及び確率の基本性質について復習しておきます。

事象

  1. 事象　　　ある試行の結果として起こる事柄

  2. 根元事象　ある試行において、起こりうる個々の場合の事象

  3. 全事象　　根元事象の全体からなる集合で表される事象

確率の定義

全事象$${U}$$のどの根元事象も同時に確からしいとき、事象$${A}$$の起こる確率は

$$
P(A)=\frac{n(A)}{n(U)}=\frac{事象Aの起こる場合の数}{起こりうるすべての場合の数}
$$

確率の基本性質

ある試行における全事象を$${U}$$、空事象を$${\emptyset}$$、事象を$${A, B}$$で表す。

  1. 基本性質　$${0 \leq P(A) \leq 1 \ \ P(\emptyset)=0 \ \ P(U)=1}$$

  2. 積事象　「事象$${A}$$と$${B}$$がともに起こる」という事象。$${ A \cap B }$$で表す。
    和事象　「事象$${A}$$または$${B}$$が起こる」という事象。　$${A \cup B }$$で表す。

  3. 加法定理　$${ A \cap B = \emptyset }$$（排反）のとき、$${ P( A \cup B) = P(A)+P(B) }$$
    和事象の確率　$${ P(A \cup B) = P(A)+P(B)-P(A \cap B) }$$
    余事象の確率　$${ P(A)+P(\bar{A}) = 1}$$すなわち$${ P(\bar{A})=1-P(A) }$$

確率を計算する

確率を計算するプログラムを作成するにあたり、今回は次のような問題を考えてみます。

問題
1から100までの番号札から1枚を取り出すとき、次の確率を求めよ。
(1)  5の倍数の札を取る確率
(2)  5の倍数または8の倍数の札を取る確率

アルゴリズム設計 

計算方法は単純に確率の定義通りに事象を数えていきます。たとえば、問題(1)であれば、「5の倍数の札を取る場合の数$${n(A)}$$」を数え、同時に「すべての札を取る場合の数$${n(U)}$$」も数えておき、最後に、これらを割り算することで、「5の倍数の札を取る確率$${P(A)}$$」を求めます。なお、「5の倍数の札を取る場合の数」は$${100 \div 5 = 20}$$と計算でき、「すべての札を取る場合の数」は計算するまでもなく、番号札の数と同じ$${100}$$となりますが、今回はプログラミングの練習を兼ねて、あえて事象を数えてみます。

プログラム

では、確率を計算するプログラムを作成していきます。

// 確率を計算する
void setup(){
  
  int card_num = 100; // 番号札の数
  int event_num = 0; // 事象が起こる場合の数
  int total_num = 0; // 起こりうるすべての場合の数
  
  for(int i=1; i<=card_num; i++){ 
    if( i%5 == 0 ){ // (1) 5の倍数の札を数える
      event_num++;
    }
    total_num++; // 起こりうるすべての場合の数を数える
  }
  float p = (float)event_num / (float)total_num; // 確率を計算
  println(p); // 確率をコンソールに出力
}

ソースコード1　確率を計算するプログラム

このソースコードを、Processingの開発環境ウィンドウを開いて（スケッチ名を「probability」としています）、テキストエディタ部分に書いて実行します。

図1　スケッチ「probability」の実行結果

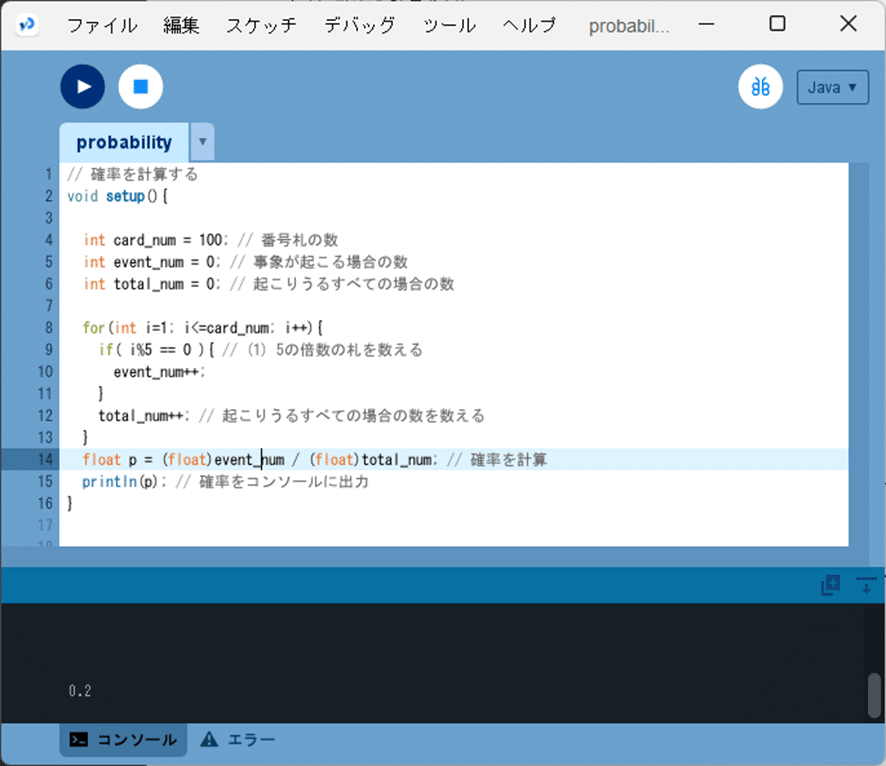
図1のように、5の倍数の札を取る確率「0.2」をコンソールに出力します。

プログラムの解説1「事象のカウント」

アルゴリズム設計のところで説明したように、今回は敢えて事象を数える方法を取っています。

  1. 「5の倍数の札を取る場合の数」を表す整数型の変数をevent_num、「すべての札を取る場合の数」を表す整数型の変数をtotal_numとして、ともに0で初期化しておきます。

  2. forループを用いて、1から100までの番号札を順に選んでいき、if文でそれが5の倍数であるか、つまり、5で割ったときの余りが0になるかを確認し、余りが0であれば、event_numを1ずつ増やします。また、同時に、total_numを１ずつ増やしていきます。

プログラムの解説2「キャスト」

ソースコード1で、「5の倍数の札を取る場合の数」（event_num）と「すべての札を取る場合の数」（total_num）を数えたあと、これらを割り算することで「5の倍数の札を取る確率」(p)を求めていますが、最後の割り算をするとき、注意が必要です。
event_numやtotal_numは数を数えるためにint型（整数型）の変数としていましたので、単純に

event_num / total_num;

としてしまうと、割り算の結果は「0」になってしまいます。これは、整数同士に対して「/」は整数の商を与えることとevent_num $${ \leq }$$ total_numであることを考慮すると、割り算の結果は0か1のどちらかとなります。これでは、今回求めたい確率にはなりません。
今回行いたい処理は、割り算でもとくに小数の割り算になります。そこで、整数を小数（浮動小数点数）として扱うようにします。それには、

(float)event_num / (float) total_num;

と、整数型の変数の前に「(float)」を付けるだけで実現できます。これを「キャスト」と呼びます（「整数型変数を浮動小数点数型にキャストする」というような言い方をします）。実際にキャストを行って処理すると、小数で結果を出力しています（図1参照）。

和事象の確率を計算する

次に、問題(2)を考えます。

アルゴリズム設計1「和事象を直接数える」

プログラムはソースコード 1とほとんど同じになります。問題(1)では「5の倍数の札を取る場合の数」を数えましたが、今回は「5の倍数または8の倍数の札を取る場合の数」を数えますので、ソースコード1のif文の条件式を

i%5 == 0 || i%8 == 0

に置き換えることだけで数えることができます。

プログラム1

では、直接数えて和事象を計算するプログラムを作成します。

// 確率を計算する
void setup(){
  
  int card_num = 100; // 番号札の数
  int event_num = 0; // 事象が起こる場合の数
  int total_num = 0; // 起こりうるすべての場合の数
  
  for(int i=1; i<=card_num; i++){ 
    if( i%5 == 0 || i%8 == 0 ){ // (2) 5の倍数または8の倍数の札を数える
      event_num++;
    }
    total_num++; // 起こりうるすべての場合の数を数える
  }
  float p = (float)event_num / (float)total_num; // 確率を計算
  println(p); // 確率をコンソールに出力
}

ソースコード2　和事象を計算するプログラム（直接数える）

このソースコードを、Processingの開発環境ウィンドウを開いて（スケッチ名を「probability_sum_event」としています）、テキストエディタ部分に書いて実行します。

図2　スケッチ「probability_sum_event」の実行結果

図2のように、5の倍数または8の倍数の札を取る確率「0.3」をコンソールに出力します。

アルゴリズム設計2「和事象の確率の基本性質を利用する」

アルゴリズム設計1では、和事象の場合の数を直接計算して確率を求めました。ここでは、確率の基本性質を利用して和事象の確率を計算してみます。つまり、「5の倍数の札を取る確率$${P(A)}$$」と「8の倍数の札を取る確率$${P(B)}$$」、そして「5の倍数でも8の倍数でもある札を取る確率$${P(A \cap B)}$$」をそれぞれ計算し、最後に、和事象の確率の基本性質である

$$
P(A \cup B) = P(A)+P(B)-P(A \cap B)
$$

を用いて、「5の倍数または8の倍数の札を取る確率$${P(A \cup B)}$$」を計算します。なお、「5の倍数でも8の倍数でもある札を取る」を表す条件式は、

i%5 == 0 && i%8 == 0

と表すことができます。

プログラム2

では、和事象の確率の基本性質を利用したプログラムを作成します。

// 確率を計算する
void setup(){
  
  int card_num = 100; // 番号札の数
  int event_A_num = 0; // 5の倍数の番号札の場合の数
  int event_B_num = 0; // 8の倍数の番号札の場合の数
  int event_AandB_num = 0; // 5の倍数でも8の倍数でもある番号札の場合の数
  int total_num = 0; // 起こりうるすべての場合の数
  
  for(int i=1; i<=card_num; i++){ 
    if( i%5 == 0 ){ // 5の倍数の札を数える
      event_A_num++;
    }
    if( i%8 == 0 ){ // 8の倍数の札を数える
      event_B_num++;
    }
    if( i%5 == 0 && i%8 == 0 ){ // 5の倍数かつ8の倍数の札を数える
      event_AandB_num++;
    }
    total_num++; // 起こりうるすべての場合の数を数える
  }
  float p_A = (float)event_A_num / (float)total_num; // 5の倍数の番号札を取る確率
  float p_B = (float)event_B_num / (float)total_num; // 8の倍数の番号札を取る確率
  // 5の倍数かつ8の倍数の番号札を取る確率
  float p_AandB = (float)event_AandB_num / (float)total_num;
  float p = p_A + p_B - p_AandB; // 和事象の確率の基本性質を利用して計算
  println(p); // 確率をコンソールに出力
}

ソースコード3　和事象の確率の基本性質を利用したプログラム

このソースコードを、Processingの開発環境ウィンドウを開いて（スケッチ名を「probability_sum_event2」としています）、テキストエディタ部分に書いて実行します。

図3　スケッチ「probability_sum_event2」の実行結果

図3のように、5の倍数または8の倍数の札を取る確率「0.29999998」をコンソールに出力します。丸め誤差を含んでいますが、結果はソースコード2の結果と同じであることがわかります。

まとめ

今回は、数学Aで学ぶ「事象と確率」について、いくつかの確率を計算するプログラムを作成しました。今回のプログラムのポイントは、場合の数を用いて確率を計算するときに、整数から小数（浮動小数点数）にキャストするところです。キャストを行わないと、正しい答えが出なくなります。
このように、データ型を意識することはプログラミングを行う上でとても大事になってきます。キャストのようなデータ型を扱う方法についても少しずつ慣れていってください。

参考文献

改訂版 教科書傍用 スタンダード 数学A（数研出版、ISBN9784410209277）


演習問題

２個のさいころを同時に投げるとき、次の確率を求めて、コンソールに出力するプログラムを作成してください。
(1) 出る目の和が$${8}$$
(2) 出る目の積が$${6}$$


演習問題の解答例

ここから先は

452字 / 1画像 / 1ファイル

この記事が気に入ったらサポートをしてみませんか？