高校数学をプログラミングで解く（数学A編）「2-4 チェバの定理、メネラウスの定理」

割引あり

MK's papa

2023年8月19日 06:02

マガジンリスト　＞　数学A編 2.図形の性質　＞　2-4 チェバの定理、メネラウスの定理

はじめに

今回は、数学Aで学ぶ「チェバの定理・メネラウスの定理」について、それぞれの定理が成り立っていることを確認するプログラムを作成します。

チェバの定理

まず、チェバの定理について、まとめておきます。

チェバの定理
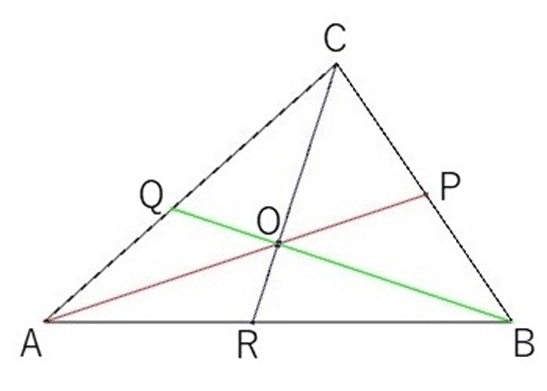
$${\triangle \mathrm{ABC}}$$の頂点$${\mathrm{A, B, C}}$$と、三角形の内部の点$${\mathrm{O}}$$を結ぶ直線$${\mathrm{AO, BO, CO}}$$が、辺$${\mathrm{BC, CA, AB}}$$と、それぞれ点$${\mathrm{P, Q, R}}$$で交わるとき、

$$
\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} = 1
$$

が成り立つ。

今回は、このチェバの定理が成り立っていることを確かめるプログラムを作成します。

アルゴリズム設計（確かめるための手順）

このチェバの定理を確かめるための手順を考えてみます。

$${\triangle \mathrm{ABC}}$$を準備する
点$${\mathrm{O}}$$の位置を決める
点$${\mathrm{P, Q, R}}$$の座標を求める
$${\mathrm{BP, PC, CQ, QA, AR, RB}}$$の長さを求める
$${\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}}}$$を計算する

最後の手順 5 で求めた値が$${1}$$になっていれば、チェバの定理が成り立っていることになります。
以下で、この手順を順番に解説していきます。

△ABCを準備する

$${\triangle \mathrm{ABC}}$$を以下のようにします。

今回は、特に$${\triangle \mathrm{ABC}}$$の辺の長さそれぞれ$${a=200, \ b=250, \ c=300 }$$とします。

頂点の座標位置
$${\triangle \mathrm{ABC}}$$の各頂点の座標位置を求めておきます。以下のように、頂点$${\mathrm{A}}$$を原点とし、頂点$${\mathrm{A}}$$と頂点$${\mathrm{B}}$$を結んだ直線を右向き正とする$${x}$$軸、その直線と垂直に交わり、頂点$${\mathrm{A}}$$を通る直線を上向き正とする$${y}$$軸とします。

その結果、頂点$${\mathrm{A}}$$の座標を$${(0,0)}$$、頂点$${\mathrm{B}}$$の座標を$${(c,0)}$$と置くことができます。また、頂点$${\mathrm{C}}$$の座標$${(x_C, y_C)}$$は

$$
x_C=\frac{b^2+c^2-a^2}{2c}, \ \ y_C=\frac{\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}{2c}
$$

と求めることができます。頂点$${\mathrm{C}}$$の座標の求め方は、別記事『高校数学をプログラミングで解く（数学A編）「2-3 三角形の五心」』で説明していますので、そちらをご覧ください。

点Oの位置を決める

次に、点$${\mathrm{O}}$$の座標位置$${(x_O, y_O)}$$を決めます。点$${\mathrm{O}}$$は三角形の内部にあればどこでも大丈夫です。今回は、$${x_O=150, \ y_O=50}$$としています。

点P,Q,Rの座標を求める

点$${\mathrm{A, B, C}}$$の座標位置と点$${\mathrm{O}}$$の座標位置を準備したので、点$${\mathrm{P, Q, R}}$$の座標位置を求めることができます（図1参照）。
点$${\mathrm{P}}$$の座標$${(x_P, y_P)}$$を求めます。点$${\mathrm{P}}$$は直線$${\mathrm{AO}}$$と直線$${\mathrm{BC}}$$との交点になります。直線$${\mathrm{AO}}$$の方程式は

$$
y=\frac{y_O}{x_O}x
$$

となり、直線$${\mathrm{BC}}$$の方程式は、

$$
y=-\frac{y_C}{c-x_C}(x-c)
$$

となるので、これらを連立方程式として解くと、

$$
x_P=\frac{y_C x_O}{(c-x_C)y_O+y_C x_O}c, \ \ y_P=\frac{y_C y_O}{(c-x_C)y_O+y_C x_O}c
$$

と求めることができます。
同様にして、点$${\mathrm{Q}}$$の座標$${(x_Q, y_Q)}$$を直線$${\mathrm{BO}}$$と直線$${\mathrm{AC}}$$との交点、点$${\mathrm{R}}$$の座標$${(x_R, y_R)}$$を直線$${\mathrm{CO}}$$と直線$${\mathrm{AB}}$$との交点として、それぞれ求めることができます。計算を省略しますが、それぞれ

$$
x_Q=\frac{x_C y_O}{y_C(c-x_O)+x_C y_O}c, \ \ y_Q=\frac{y_C y_O}{y_C(c-x_O)+x_C y_O}c
$$

及び

$$
x_R=\frac{y_C x_O - x_C y_O}{y_C-y_O}, \ \ y_R=0
$$

と求めることができます。

BP, PC, CQ, QA, AR, RBの長さを求める

頂点$${\mathrm{A,B,C}}$$及び点$${\mathrm{P,Q,R}}$$の座標位置がわかりましたので、チェバの定理に出てくる線分の長さを求めます。

$$
\mathrm{BP} = \sqrt{(c-x_P)^2+y_P^2}, \ \ \mathrm{PC}=\sqrt{(x_C-x_P)^2+(y_C-y_P)^2} \\ \mathrm{CQ}=\sqrt{(x_C-x_Q)^2+(y_C-y_Q)^2}, \ \ \mathrm{QA}=\sqrt{x_Q^2+y_Q^2} \\ \mathrm{AR} = |x_R|, \ \ \mathrm{RB}=|c-x_R|
$$

BP/PC ・ CQ/QA・AR/RBを計算する

最後に、チェバの定理の式に出てくる

$$
\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}}
$$

を計算します。計算結果が$${1}$$になっていれば、チェバの定理が成り立っていることになります。

チェバの定理を確かめるためのプログラム

ここまで説明してきたことをプログラミングしてみます。

// チェバの定理を確かめる
void setup(){
  size(650,650); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する
  background(255,255,255); // 背景を白色にする
  noFill(); // 図形の塗りつぶしなし
  noLoop(); // 繰り返し処理をしない
  
  // 三角形の辺の長さ
  float a, b, c; 
  a = 200.0;
  b = 250.0;
  c = 300.0;
  
  // 三角形の頂点の座標
  float A_x, A_y, B_x, B_y, C_x, C_y;
  A_x = 0.0;
  A_y = 0.0;
  B_x = c;
  B_y = 0.0;
  C_x = (c*c + b*b - a*a) / 2.0 / c;
  C_y = sqrt( (a+b+c) * (-a+b+c) * (a-b+c) * (a+b-c) ) / 2.0 / c;
  
  // 三角形を描く
  triangle(A_x, A_y, B_x, B_y, C_x, C_y);

  // 三角形の内部の点Oを決める
  float O_x, O_y;
  O_x = 150.0;
  O_y = 50.0;
  strokeWeight(5);
  point(O_x, O_y); // 点Oをプロットする

  //点Pの座標
  float P_x, P_y;
  P_x = C_y * O_x / ( (c-C_x) * O_y + C_y * O_x ) * c;
  P_y = C_y * O_y / ( (c-C_x) * O_y + C_y * O_x ) * c;
  stroke(255,0,0);
  strokeWeight(3);
  point(P_x, P_y); // 点Pをプロットする
  strokeWeight(1);
  line(A_x, A_y, P_x, P_y); // 線分APを描く
  
  // 点Qの座標
  float Q_x, Q_y;
  Q_x = C_x * O_y / ( C_y * (c - O_x) + C_x * O_y ) * c;
  Q_y = C_y * O_y / ( C_y * (c - O_x) + C_x * O_y ) * c;
  stroke(0,255,0);
  strokeWeight(3);
  point(Q_x, Q_y); // 点Qをプロットする
  strokeWeight(1);
  line(B_x, B_y, Q_x, Q_y); // 線分BQを描く
  
  // 点Rの座標
  float R_x, R_y;
  R_x = ( C_y * O_x - C_x * O_y ) / (C_y - O_y);
  R_y = 0.0;
  stroke(0,0,255);
  strokeWeight(3);
  point(R_x, R_y); // 点Rをプロットする
  strokeWeight(1);
  line(C_x, C_y, R_x, R_y); // 線分CRを描く
  
  // 各辺の長さ
  float BP, PC;
  BP = sqrt( (c-P_x) * (c-P_x) + P_y * P_y );
  PC = sqrt( (C_x-P_x) * (C_x-P_x) + (C_y-P_y) * (C_y-P_y) );
  float CQ, QA;
  QA = sqrt( Q_x * Q_x + Q_y * Q_y );
  CQ = sqrt( (C_x-Q_x) * (C_x-Q_x) + (C_y-Q_y) * (C_y-Q_y) );
  float AR, RB;
  AR = abs(R_x);
  RB = abs(c - R_x);
  
  println("BP", BP);
  println("PC", PC);
  println("CQ", CQ);
  println("QA", QA);
  println("AR", AR);
  println("RB", RB);
  println("(BP / PC) * (CQ / QA) * (AR / RB) =", (BP / PC) * (CQ / QA) * (AR / RB) ); 
  
}

ソースコード1　チェバの定理を確かめるためのプログラム

このソースコードを、Processingの開発環境ウィンドウを開いて（スケッチ名を「Cevastheorem」としています）、テキストエディタ部分に書いて実行すると、実行ウィンドウのキャンバスに点$${\mathrm{O}}$$と点$${\mathrm{P,Q,R}}$$の位置、及び線分$${\mathrm{AP, BQ, CR}}$$が描画されます。

なお、ここまでの三角形や各点の位置、及び線分の描画は、チェバの定理を確かめるためだけであれば必要ないのですが、正しくプログラミングができているかを確かめるために描いてみました。図5を見ると、線分$${\mathrm{AP, BQ, CR}}$$が点$${\mathrm{O}}$$で期待通りに交わっていることを見ることができます。これを確かめることで、プログラムはおそらく正しく記述できていると考えることができます。

そして、開発環境ウィンドウのコンソールには、線分$${\mathrm{BP, PC, CQ, QA, AR, RB}}$$の長さと、$${\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}}}$$の値が出力されています。

この結果をみると、

$$
\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}}
$$

の値が「1.0」となっており、チェバの定理が成り立っていることがわかります。なお、結果の値が「1.0000001」となっていますが、これは浮動小数点数の丸め誤差ですので、1に近い値が出ていれば、正しい結果と考えることができます。

チェバの定理の考察

今回は、三角形の内部の点$${\mathrm{O}}$$を$${x_O=150, \ y_O=50}$$としましたが、この座標位置でたまたまチェバの定理が成り立ったかもしれません。そこで、点$${\mathrm{O}}$$の座標位置を変えてみてもチェバの定理が成り立っていることを確かめてみてください。
また、点$${\mathrm{O}}$$が三角形の辺の上にある場合や三角形の頂点と一致する場合、三角形の外部にある場合など、結果の値がどうなるか、そしてどうしてそうなるのかを考えてみるのは勉強になると思いますので、こちらもぜひチャレンジしてみてください。

メネラウスの定理

次は、メネラウスの定理です。こちらもまとめておきます。

メネラウスの定理
$${\triangle \mathrm{ABC}}$$の辺$${\mathrm{BC, CA, AB}}$$またはその延長が、三角形の頂点を通らない１つの直線$${l}$$ と、それぞれ点$${\mathrm{P,Q,R}}$$で交わるとき、

$$
\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} = 1
$$

が成り立つ。

今度は、このメネラウスの定理が成り立っていることを確かめるプログラムを作成します。

アルゴリズム設計（確かめるための手順）

この定理を確かめるための手順を考えてみます。チェバの定理とほとんど同じです。

$${\triangle \mathrm{ABC}}$$を準備する
直線$${l}$$を決める
点$${\mathrm{P, Q, R}}$$の座標を求める
$${\mathrm{BP, PC, CQ, QA, AR, RB}}$$の長さを求める
$${\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}}}$$を計算する

最後の手順 5 で求めた値が$${1}$$になっていれば、メネラウスの定理が成り立っていることになります。
以下で、この手順を順番に解説していきます。

△ABCを準備する

$${\triangle \mathrm{ABC}}$$は、チェバの定理で利用した三角形と同じものを利用します。

直線lを決める

直線$${l}$$の方程式を傾き$${m}$$、切片$${n}$$として、

$$
y=mx+n
$$

で表すことにします。今回は、$${m=-0.6, \ \ n=200}$$としました。

点P, Q, Rの座標を求める

点$${\mathrm{A, B, C}}$$の座標位置と直線$${l}$$を準備したので、点$${\mathrm{P, Q, R}}$$の座標位置を求めることができます（図7参照）。
点$${\mathrm{P}}$$の座標$${(x_P, y_P)}$$を求めます。点$${\mathrm{P}}$$は直線$${l}$$と直線$${\mathrm{BC}}$$との交点になります。
直線$${\mathrm{BC}}$$の方程式は、

$$
y=-\frac{y_C}{c-x_C}(x-c)
$$

となるので、直線$${l}$$との連立方程式として解くと、

$$
x_P=\frac{y_Cc-n(c-x_C)}{m(c-x_C)+y_C}, \ \ y_P = \frac{(mc+n)y_C}{m(c-x_C)+y_C}
$$

と求めることができます。
同様にして、点$${\mathrm{Q}}$$の座標$${(x_Q, y_Q)}$$を直線$${l}$$と直線$${\mathrm{AC}}$$との交点、点$${\mathrm{R}}$$の座標$${(x_R, y_R)}$$を直線$${l}$$と直線$${\mathrm{AB}}$$との交点として、それぞれ求めることができます。計算を省略しますが、それぞれ

$$
x_Q=\frac{nx_C}{y_C-mx_C}, \ \ y_Q=\frac{ny_C}{y_C-mx_C}
$$

及び

$$
x_R=-\frac{n}{m}, \ \ y_R=0
$$

と求めることができます。

BP, PC, CQ, QA, AR, RBの長さを求める

頂点$${\mathrm{A, B, C}}$$及び点$${\mathrm{P, Q, R}}$$の座標位置がわかりましたので、メネラウスの定理に出てくる線分の長さを求めます。

$$
\mathrm{BP}=\sqrt{(c-x_P)^2+y_P^2}, \ \ \mathrm{PC}=\sqrt{(x_C-x_P)^2+(y_C-y_P)^2} \\ \mathrm{CQ} = \sqrt{(x_C-x_Q)^2+(y_C-y_Q)^2}, \ \ \mathrm{QA}=\sqrt{x_Q^2+y_Q^2} \\
\mathrm{AR}=|x_R|, \ \ \mathrm{RB}=|c-x_R|
$$

BP/PC ・ CQ/QA・AR/RBを計算する

最後に、メネラウスの定理の式に出てくる

$$
\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}}
$$

を計算します。計算結果が$${1}$$になっていれば、メネラウスの定理が成り立っていることになります。

メネラウスの定理を確かめるためのプログラム

ここまで説明してきたことをプログラミングしてみます。

// メネラウスの定理を確かめる
void setup(){
  size(700, 700); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する
  background(255,255,255); // 背景を白色にする
  noFill(); // 図形の塗りつぶしなし
  noLoop(); // 繰り返し処理をしない
  
  // 三角形の辺の長さ
  float a, b, c; 
  a = 200.0;
  b = 250.0;
  c = 300.0;
  
  // 三角形の頂点の座標
  float A_x, A_y, B_x, B_y, C_x, C_y;
  A_x = 0.0;
  A_y = 0.0;
  B_x = c;
  B_y = 0.0;
  C_x = (c*c + b*b - a*a) / 2.0 / c;
  C_y = sqrt( (a+b+c) * (-a+b+c) * (a-b+c) * (a+b-c) ) / 2.0 / c;
  
  // 三角形を描く
  triangle(A_x, A_y, B_x, B_y, C_x, C_y);

  // 直線lを決める
  float m, n;
  m = -3.0/5.0;
  n = 200.0;
  line(0.0, n, 400.0, m*400.0+n); // 直線lを描く

  //点Pの座標
  float P_x, P_y;
  P_x = (C_y * c - n * (c-C_x)) / ( m * (c-C_x) + C_y );
  P_y = (m * c + n) * C_y / ( m * (c-C_x) + C_y );
  stroke(255,0,0);
  strokeWeight(5);
  point(P_x, P_y); // 点Pをプロットする
  
  // 点Qの座標
  float Q_x, Q_y;
  Q_x = n * C_x / ( C_y - m * C_x );
  Q_y = n * C_y / ( C_y - m * C_x );
  stroke(0,255,0);
  strokeWeight(5);
  point(Q_x, Q_y); // 点Qをプロットする
  
  // 点Rの座標
  float R_x, R_y;
  R_x = -n / m;
  R_y = 0.0;
  stroke(0,0,255);
  strokeWeight(5);
  point(R_x, R_y); // 点Rをプロットする
  
  // 各辺の長さ
  float BP, PC;
  BP = sqrt( (c-P_x) * (c-P_x) + P_y * P_y );
  PC = sqrt( (C_x-P_x) * (C_x-P_x) + (C_y-P_y) * (C_y-P_y) );
  float CQ, QA;
  QA = sqrt( Q_x * Q_x + Q_y * Q_y );
  CQ = sqrt( (C_x-Q_x) * (C_x-Q_x) + (C_y-Q_y) * (C_y-Q_y) );
  float AR, RB;
  AR = abs(R_x);
  RB = abs(c - R_x);
  
  println("BP", BP);
  println("PC", PC);
  println("CQ", CQ);
  println("QA", QA);
  println("AR", AR);
  println("RB", RB);
  println("(BP / PC) * (CQ / QA) * (AR / RB) =", (BP / PC) * (CQ / QA) * (AR / RB) ); 
 
}

ソースコード2　メネラウスの定理を確かめるためのプログラム

このソースコードを、Processingの開発環境ウィンドウを開いて（スケッチ名を「Menelaustheorem」としています）、テキストエディタ部分に書いて実行すると、実行ウィンドウのキャンバスに直線$${l}$$と点$${\mathrm{P, Q, R}}$$の位置が描画されます。

この結果をみると、

$$
\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}}
$$

の値が丸め誤差を無視して「1.0」となっており、メネラウスの定理が成り立っていることがわかります。

メネラウスの定理の考察

チェバの定理の時と同様に、メネラウスの定理について直線$${l}$$を変えてみても成り立っていることを確かめることは必要です。ぜひやってみてください。
そのとき、直線$${l}$$が$${\triangle \mathrm{ABC}}$$の内部を通らない場合、直線$${l}$$が$${\triangle \mathrm{ABC}}$$の頂点を通る場合、直線$${l}$$が$${\triangle \mathrm{ABC}}$$のいずれかの辺と並行になる場合なども考えてみるとよいと思います。

まとめ

今回は、数学Aで学ぶ「チェバの定理、メネラウスの定理」について、それらの定理が実際に成り立っているのかをプログラムを作って確かめてみました。具体的に、線分$${\mathrm{BP, PC, CQ, QA, AR, RB}}$$の長さを求めた結果を見ると、それらの長さにあまり関連がなさそうに見えますが、

$$
\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}}
$$

を計算してみると、「1」になっていることはちょっと不思議な感じがしたのではないでしょうか。
あと最後に念のため言っておくと、今回行ったことは成り立つことをいくつかの例を使って確かめただけで、これらの定理が成り立つことを証明したわけではないことに注意してください。
なお、証明はそんなに難しくないようですので、一度チャレンジしてみてください。

参考文献

改訂版教科書傍用スタンダード数学A（数研出版、ISBN9784410209277）

演習問題

チェバの定理の逆を用いて、三角形の３つの頂角の２等分線は１点で交わることを示してください（図11）。

ヒント

チェバの定理の逆
$${\triangle \mathrm{ABC}}$$の辺$${\mathrm{BC, CA, AB}}$$上に、それぞれ点$${\mathrm{P, Q, R}}$$があり、

$$
\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}} = 1
$$

が成り立てば、３直線$${\mathrm{AP, BQ, CR}}$$は１点で交わる。

この演習問題が成り立つことを示すプログラムは、線分$${AR, RB, BP, PC, CQ, QA}$$の長さを求めて、

$$
\frac{\mathrm{BP}}{\mathrm{PC}} \cdot \frac{\mathrm{CQ}}{\mathrm{QA}} \cdot \frac{\mathrm{AR}}{\mathrm{RB}}
$$

を計算し、その結果をコンソールに出力するものを作成します。このときの出力結果が$${1}$$となっていれば、チェバの定理の逆から、三角形の３つの頂角の２等分線は１点で交わることがわかります。

演習問題の解答例

ここから先は

540字 / 1画像 / 1ファイル

ログイン

この記事が気に入ったらチップで応援してみませんか？