高校数学をプログラミングで解く（数学Ａ編）「2-0 高校数学に適した座標系の準備」

マガジンリスト　＞　数学A編 2.図形の性質　＞　2-0 高校数学に適した座標系の準備

はじめに

今回は、「高校数学をプログラミングで解く」で図形を描いていくにあたり、Processingの座標系を高校数学に適したものにする手順をまとめておきます。

座標系について（復習）

Processingの実行ウィンドウのキャンバスに設定される座標系について、別記事『高校数学をプログラミングで解く（準備編）「1-2 プログラムを書く」』で説明しました。これを再掲しておきます。

実行ウィンドウのキャンバスには以下のような座標系が設定されています。

図1　キャンバスの座標系

キャンバスの左上の画素を原点$${(0,0)}$$とし、右向きに$${x}$$軸の正の向き、下向きに$${y}$$軸の正の向きとする座標系となります。たとえば、記事『高校数学をプログラミングで解く（準備編）「1-2 プログラムを書く」』で作成したスケッチ「drawCircle」のキャンバスを見てみます。以下の zip ファイルをダウンロードして展開または解凍してください。

drawCircle.zip

447 Bytes

ファイルダウンロードについて

ダウンロード

スケッチ「drawCircle」のキャンバス（図1）は縦に300個、横に300個の画素が敷き詰められたものですので、右上の画素は$${(299,0)}$$、左下の画素は$${(0,299)}$$、右下の画素は$${(299,299)}$$と表すことができます。左上の原点となる画素を$${(0,0)}$$としているので、右下の画素の座標は$${(300,300)}$$ではなく、$${(299,299)}$$になることに注意が必要です。また、高校数学では通常、上向きを$${y}$$軸の正の向きとしますので、Processingでグラフなどを描かせるときには注意が必要です。

高校数学に適した座標系の準備

前節の最後で書いたように、高校数学では通常、上向きを$${y}$$軸の正の向きとします。そこで、キャンバスの座標系の$${y}$$軸の正の向きが上向きとなるようにします。また、座標系の原点が実行ウィンドウのキャンバスの中心になるように移動させます。

高校数学に適した座標系

キャンバスの中心の画素を原点$${(0,0)}$$とし、右向きに$${x}$$軸の正の向き、上向きに$${y}$$軸の正の向きとする座標系を準備するためには、プログラムの先頭に下記のコードを加えることで実現できます。

// 高校数学に適した座標系
void setup(){
  size(300, 300); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する
  background(255,255,255); // 背景を白色にする
  noFill(); // 図形の塗りつぶしなし
  noLoop(); // 繰り返し処理をしない
  
  // 以下に図形を描く

}

ソースコード1　高校数学に適した座標系を準備するコード

座標系の解説

以下で、このソースコード1について解説していきます。
解説を行うために、辺の比が3:4:5となる直角三角形$${\mathrm{ABC}}$$を利用します。具体的には実行ウィンドウのキャンバスを300×300で用意し、頂点$${\mathrm{A}}$$を$${(100,0)}$$、頂点$${\mathrm{B}}$$を$${(0,75)}$$、頂点$${\mathrm{C}}$$を$${(0,0)}$$とする直角三角形を描きます。

// 直角三角形を描く
void setup(){
  size(300, 300); // キャンバスの大きさを指定する

  // 直角三角形の3つの頂点を指定
  float A_x = 100.0;
  float A_y = 0.0;
  float B_x = 0.0;
  float B_y = 75.0;
  float C_x = 0.0;
  float C_y = 0.0;
  triangle(A_x, A_y, B_x, B_y, C_x, C_y); // 直角三角形を描画
}

ソースコード2　直角三角形を描くプログラム

このソースコード2を、Processingの開発環境ウィンドウを開いて（スケッチ名を「prepareCoordinateSystem」としています）、テキストエディタ部分に書いて実行します。

図2　左上に直角三角形が描かれる

図2のように、直角三角形が左上の位置に描かれます。これに座標系を付けたものを以下に示します。

図3　最初の座標系

translate 関数

まず、座標系の位置を変更します。この場合、translate 関数を利用します。

translate(x, y);

各引数は次のようになっています。

x：$${x}$$方向の正の向きに移動させる幅　float型
y：$${y}$$方向の正の向きに移動させる幅　float型

ソースコード2にこの translate 関数を導入してみます。translate 関数の１つ目の引数に与える値をキャンバスの幅 width の半分、2つ目の引数に与える値をキャンバスの高さ height の半分に設定することで、座標系の位置をキャンバスの中心に移動させます。

// 直角三角形を描く
void setup(){
  size(300, 300); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する

  // 直角三角形の3つの頂点を指定
  float A_x = 100.0;
  float A_y = 0.0;
  float B_x = 0.0;
  float B_y = 75.0;
  float C_x = 0.0;
  float C_y = 0.0;
  triangle(A_x, A_y, B_x, B_y, C_x, C_y); // 直角三角形を描画
}

ソースコード3　translate 関数を導入

先ほどのスケッチ「prepareCoordinateSystem」をソースコード3に書き換えて実行してみます。

図4　座標系の移動

図4のように、直角三角形がキャンバスの左上から中央付近に移動しています。これは translate 関数によって座標変換がなされた結果です。この段階での座標系は、以下のようになっています。

図5　原点がキャンバスの中央に移動した座標系

width, height変数について

なお、ソースコード3で translate 関数を利用した際、引数に width と height という変数を使っています。これらの変数はそれぞれ実行ウィンドウのキャンバスの幅と高さを表すもので、size 関数を呼び出したときに、自動的に設定されます。size 関数の１つ目の引数の値が width（幅）に設定され、2つ目の引数の値が height（高さ）に設定されます。
width と height は特別な変数で、宣言する必要はありません。

scale 関数

次に、$${y}$$軸の正の向きを下向きから上向きに変更します。これを行うために、scale 関数を利用します。scale 関数は図形の拡大縮小を行うための関数になります。

scale(x, y);

各引数は次のようになっています。

x：$${x}$$方向への拡大縮小の比率　float型
y：$${y}$$方向への拡大縮小の比率　float型

引数の値はマイナスの値を取ることができます。マイナスの値の場合、図形はその方向に反転する形になります。この性質を利用することで座標系を$${y}$$軸方向に反転させることができます。

// 直角三角形を描く
void setup(){
  size(300, 300); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する

  // 直角三角形の3つの頂点を指定
  float A_x = 100.0;
  float A_y = 0.0;
  float B_x = 0.0;
  float B_y = 75.0;
  float C_x = 0.0;
  float C_y = 0.0;
  triangle(A_x, A_y, B_x, B_y, C_x, C_y); // 直角三角形を描画
}

ソースコード4　scale 関数を導入

スケッチ「prepareCoordinateSystem」をソースコード4に書き換えて実行してみます。

図6　座標系の反転

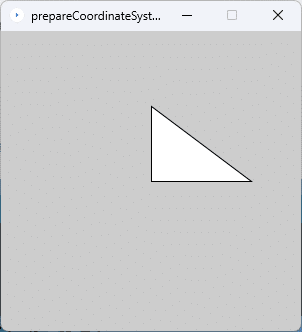
図6のように、直角三角形が$${y}$$方向に反転しています。これは scale 関数によって座標変換がなされた結果です。これで座標系は、以下のように右向きに$${x}$$軸の正の向き、上向きに$${y}$$軸の正の向きとする座標系になっています。

図6　右向きにx軸の正の向き、上向きにy軸の正の向きとする座標系

その他、background 関数、noFill 関数、noLoop 関数

ソースコード4の段階で、右向きに$${x}$$軸の正の向き、上向きに$${y}$$軸の正の向きとする、高校数学に適した座標系が得られましたが、もう少し追加しておきます。
1つ目は

background(255, 255, 255);

を導入して、背景色を白色にしておきます。background 関数の詳細は『高校数学をプログラミングで解く（準備編）「2-2 Processingで色を扱う」』で説明していますので、そちらをご覧ください。
2つ目は、

noFill();

を導入して、描いた図形の中身は塗りつぶさないようにします。noFill 関数の詳細についても『高校数学をプログラミングで解く（準備編）「2-2 Processingで色を扱う」』で説明していますので、そちらをご覧ください。
3つ目は、

noLoop();

です。この noLoop 関数は、本来 draw 関数の処理を一度だけ行いたいときに導入するものです。今回は draw 関数を利用していませんが、Processingとそれを利用しているコンピュータとの相性によってはキャンバスに描いた図形がちかちかと点滅することがあり、それを防ぐために noLoop 関数を念のため導入しています。

最後に、これらの関数も導入して、高校数学に適した座標系をまとめてみます。

// 直角三角形を描く
void setup(){
  size(300, 300); // キャンバスの大きさを指定する
  translate(width/2, height/2); // 座標の中心をキャンバスの中心に移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する
  background(255,255,255); // 背景を白色にする
  noFill(); // 図形の塗りつぶしなし
  noLoop(); // 繰り返し処理をしない

  // 直角三角形の3つの頂点を指定
  float A_x = 100.0;
  float A_y = 0.0;
  float B_x = 0.0;
  float B_y = 75.0;
  float C_x = 0.0;
  float C_y = 0.0;
  triangle(A_x, A_y, B_x, B_y, C_x, C_y); // 直角三角形を描画
}

ソースコード5　高校数学に適した座標系

スケッチ「prepareCoordinateSystem」をソースコード5に書き換えて実行してみます。

図7　高校数学に適した座標系での直角三角形

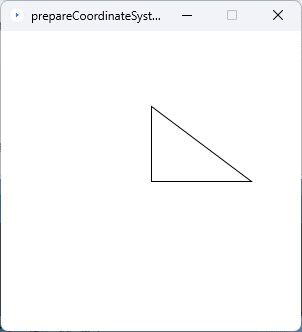
図7のように、背景が白色で、図形の中身が透明になった直角三角形が描かれます。

まとめ

今回は、「高校数学をプログラミングで解く」で図形を描いていくにあたり、Processingの座標系を高校数学に適したものにする手順をまとめました。
以降の記事で図形を描く場合は、特に断らずに setup 関数の先頭にソースコード1を導入し、高校数学に適した座標系を利用していきます。ここで紹介したソースコードの解説は特に覚えておく必要はないです。何度も図形を書いていく間に慣れていってもらえればよいです。

参考文献

Processingをはじめよう 第２版（オライリー・ジャパン、オーム社、ISBN9784873117737）