高校数学をプログラミングで解く（数学B編）「3-1 数列と一般項、等差数列」

2024年6月27日 18:00

マガジンリスト　＞　数学B編 3.数列　＞　3-1 数列と一般項、等差数列

はじめに

今回は、数学Bで学ぶ「等差数列」について、等差数列を計算してその値を出力するプログラムを２つ作成します。

等差数列

まず、等差数列とその性質についてまとめておきます。

① 定義　$${a_{n+1}=a_n+d}$$すなわち$${a_{n+1}-a_n=d}$$　$${d}$$：公差
② 一般項　初項$${a}$$、公差$${d}$$の等差数列$${ \{a_n\} }$$の一般項　$${a_n=a+(n-1)d}$$
③ 等差数列をなす3数　数列$${a,b,c}$$が等差数列$${\Leftrightarrow 2b=a+c}$$

以下で、等差数列についての問題をプログラミングして考えてみます。

等差数列の第n項の値を計算する

まず、等差数列の第$${n}$$項を計算して、開発環境ウィンドウの下部のコンソールにその値を表示するプログラムを作成します。その際、等差数列の一般項を関数として準備します。

問題1
初項$${5}$$、公差$${-2}$$の等差数列の第$${6}$$項の値を求めよ。

問題1の値を求めるプログラムは以下のようになります。

// 等差数列の第n項の値を求めてコンソールに出力
void setup(){
  
  float a = 5.0; // 初項
  float d = -2.0; // 公差
  int n = 6; // 第n項
  
  float a_n = calc_arithmetical_progression(a,d,n);
  println(a_n);
}

// 初項a,公差dの等差数列の第n項を求める関数（一般項）
float calc_arithmetical_progression(
  float a, // 初項
  float d, // 公差
  int n // 第n項
){
  return a + (n-1)*d;
}

ソースコード1　等差数列の第$${n}$$項を求めるプログラム

今回は、等差数列の一般項を利用して、初項$${a}$$,公差$${d}$$の等差数列の第$${n}$$項を求める関数 calc_arithmetical_progression を作成しました。calc_arithmetical_progression 関数は引数として、
a：初項　float型
d：公差　float型
n：第$${n}$$項　int型
の3つを取ります。また、返り値は等差数列の第$${n}$$項の値を返します。

ソースコード1を、Processingの開発環境ウィンドウを開いて（スケッチ名を「arithmetical_progression」としています）、テキストエディタ部分に書いて実行すると、開発環境ウィンドウのコンソール部分に「-5.0」と出力されます（図1）。

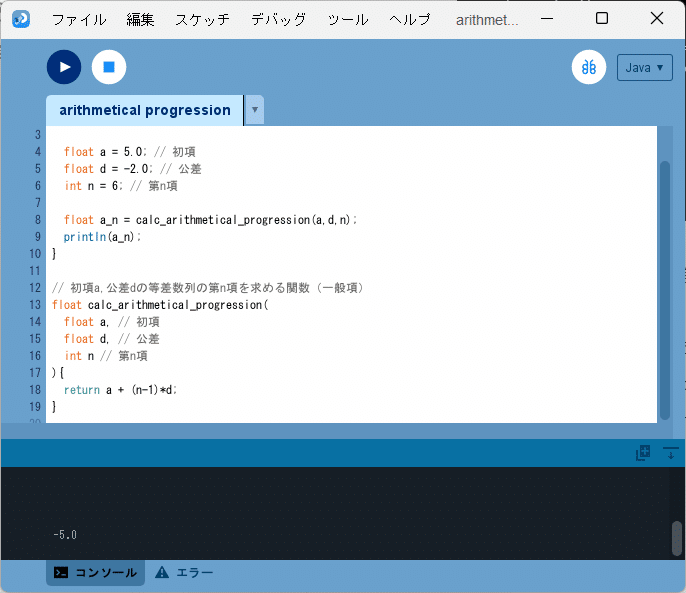
等差数列を第n項まで求める

次に、等差数列を第$${n}$$項まで計算して、開発環境ウィンドウの下部のコンソールにそれらの値を表示するプログラムを作成します。その際、スケッチ「arithmetical_progression」（ソースコード1）で作成した、初項$${a}$$,公差$${d}$$の等差数列の第$${n}$$項を求める関数 calc_arithmetical_progression を再利用します。

問題2
初項$${3}$$、公差$${4}$$の等差数列を第$${10}$$項まで求めよ。

問題2の等差数列を求めるプログラムは以下のようになります。

// 等差数列を第n項まで求めてコンソールに出力
void setup(){
  
  float a = 3.0; // 初項
  float d = 4.0; // 公差
  int n = 10; // 第n項
  
  for(int i=1; i<=n; i++){
    println(calc_arithmetical_progression(a,d,i));
  }
}

// 初項a,公差dの等差数列の第n項を求める関数（一般項）
float calc_arithmetical_progression(
  float a, // 初項
  float d, // 公差
  int n // 第n項
){
  return a + (n-1)*d;
}

ソースコード2　等差数列を第$${n}$$項まで求めるプログラム

今回は、forループを利用して calc_arithmetical_progression 関数を繰り返し呼び出すことで、第$${1}$$項から第$${10}$$項までの等差数列の値を順に計算し、コンソールに出力するようにしています。

ソースコード2を、Processingの開発環境ウィンドウを開いて（スケッチ名を「arithmetical_progression2」としています）、テキストエディタ部分に書いて実行すると、開発環境ウィンドウのコンソール部分に

3.0
7.0
11.0
15.0
19.0
23.0
27.0
31.0
35.0
39.0

と出力されます（図2）。

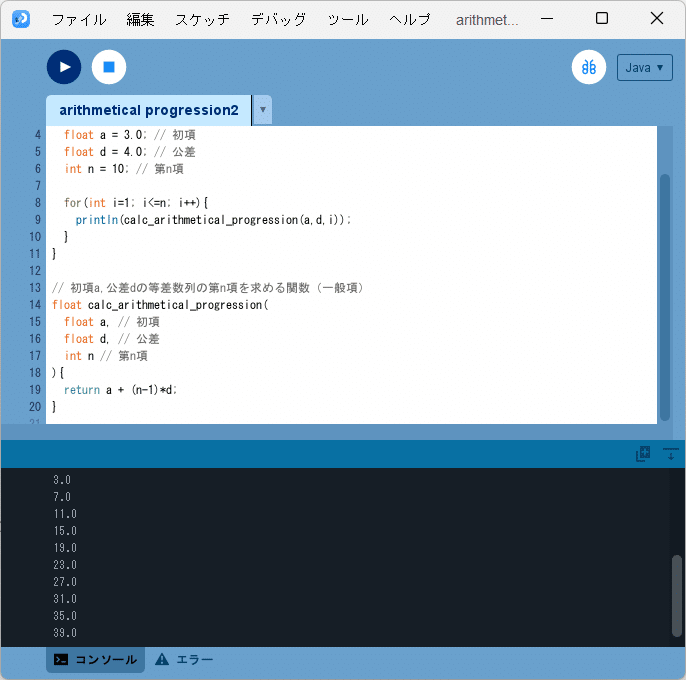
まとめ

今回は、数学Bで学ぶ「等差数列」について、等差数列を計算してその値を出力するプログラムを２つ作成しました。1つ目は、等差数列の第$${n}$$項を計算してその値をコンソールに出力プログラム、2つ目は、等差数列を第$${n}$$項まで計算してそれらの値をコンソールに出力するプログラムを作成しました。これまでの記事を読んでいただいた方は比較的簡単に感じたのではないでしょうか。そう感じられた方はプログラミングする力がついてきている証拠でしょう。

これらのプログラムを作成するにあたり、共通で利用する初項$${a}$$,公差$${d}$$の等差数列の第$${n}$$項を求める部分については関数化（calc_arithmetical_progression）して再利用できるようにしました。今回
は行っていませんが、関数の再利用を行う場合は、別ファイルに保存しておくとさらに便利になります。そのやり方については記事『高校数学をプログラミングで解く（準備編）「3-3 pdeファイルの再利用」』で詳しく紹介していますので、そちらをご覧ください。

参考文献

改訂版教科書傍用スタンダード数学B（数研出版、ISBN9784410209468）