高校数学をプログラミングで解く（数学A編）「2-5 三角形の辺と角」

割引あり

2023年8月23日 06:08

マガジンリスト　＞　数学A編 2.図形の性質　＞　2-5 三角形の辺と角

はじめに

今回は、数学Aで学ぶ「三角形の辺と角」における三角形の3辺の長さの性質を利用して、与えられた線分を3辺にもつ三角形が存在するかどうかの判定プログラムを作成し、さらに三角形が存在する場合はその三角形をキャンバス上に描くプログラムを作成します。

三角形の3辺の長さの性質

まず、三角形の存在判定を行うために、三角形の3辺の長さの性質をまとめておきます。

三角形の3辺の長さの性質
① 1つの三角形において、2辺の長さの和は、他の1辺の長さより大きい。
② 1つの三角形において、2辺の長さの差は、他の1辺の長さより小さい。

今回は、①の性質を使って、三角形の存在判定のプログラムを作成し、以下の問題を解いていきます。

問題　次の長さの線分を３辺とする三角形が存在するかどうかを調べよ。
(1) 3, 4, 6
(2) 2, 3, 6
(3) 5, 7, 8
(4) 4, 5, 9

三角形の存在判定

三角形の成立条件

三角形の3辺の長さの性質①を式で表してみます。3つの線分の長さを$${a,b,c}$$とします。

このとき、

$$
a<b+c \\
b<c+a \\
c<a+b
$$

が成り立つならば、$${a,b,c}$$を3辺にもつ三角形を作ることができます。つまり、この3つの条件を満たすことが三角形の成立条件となるわけです。

三角形の存在判定プログラム

問題(1)を例にして、三角形の存在判定プログラムを書いてみます。

// 三角形の存在判定プログラム
void setup(){
  
  // 三角形の3つの辺の長さa,b,c
  float a, b, c;
  a = 3.0;
  b = 4.0;
  c = 6.0;
 
  // 辺の長さがa,b,cとなる三角形が存在するか
  if( ( a < b+c ) && ( b < c+a ) && ( c < a+b ) ){
    println("三角形が存在する");
  } else {
    println("三角形が存在しない");
  }
}

ソースコード1　三角形の存在判定プログラム

ポイントは、$${a,b,c}$$の3つの条件すべてが成り立つときに三角形が存在するので、プログラムの判定条件は

( a < b+c ) && ( b < c+a ) && ( c < a+b )

と、「&&」（かつ）でつないで書く必要があるということです。これで、3つの条件すべてが成り立つときは「三角形が存在する」となり、3つの条件式のうち１つでも成立しなければ「三角形が存在しない」ということになります。

ソースコード1を、Processingの開発環境ウィンドウを開いて（スケッチ名を「existTriangle」としています）、テキストエディタ部分に書いて実行すると、三角形の存在判定結果がコンソールに出力されます。

問題(2)(3)(4)についても、ソースコード1の$${a,b,c}$$の値を変更することで、三角形の存在判定を行うことができます。ちなみに、(2)「三角形が存在しない」(3)「三角形が存在する」　(4)「三角形が存在しない」という判定結果がコンソールに出力されるはずです。

存在する場合は三角形を描く

三角形が存在することがわかっただけでは面白くないので、三角形が存在する場合は三角形を描くようにします。

三角形を描く方法

三角形を描く方法として、記事『高校数学をプログラミングで解く（数学A編）「2-3 三角形の五心」』の『三角形を準備する』の節で紹介したものを利用します。
図1のような3つの辺の長さが$${a,b,c}$$となる$${\triangle \mathrm{ABC}}$$に対して、以下のように、頂点$${\mathrm{A}}$$を原点とし、頂点$${\mathrm{A}}$$と頂点$${\mathrm{B}}$$を結んだ直線を右向き正とする$${x}$$軸、その直線と垂直に交わり、頂点$${\mathrm{A}}$$を通る直線を上向き正とする$${y}$$軸とします。

その結果、頂点$${\mathrm{A}}$$の座標を$${(0,0)}$$、頂点$${\mathrm{B}}$$の座標を$${(c,0)}$$と置くことができます。また、頂点$${\mathrm{C}}$$の座標$${(x_C, y_C)}$$は

$$
x_C=\frac{b^2+c^2-a^2}{2c}, \ \ y_C=\frac{\sqrt{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}{2c}
$$

となります。
$${\triangle \mathrm{ABC}}$$の各頂点の座標がわかったので、triangle 関数を利用すれば三角形を描くことができます。

三角形が存在する場合三角形を描くプログラム

では、三角形が存在する場合にはその三角形を描くプログラムを作成します。

// 三角形の存在判定を行い、存在する場合は三角形を描くプログラム
void setup(){
  size(500, 500); // キャンバスの大きさを指定する
  translate(width/5.0, height*4.0/5.0); // 座標の中心を移動する
  scale(1,-1); // y軸正の向きを下向きから上向きに反転する
  background(255,255,255); // 背景を白色にする
  noFill(); // 図形の塗りつぶしなし
  noLoop(); // 繰り返し処理をしない

  // 三角形の3つの辺の長さa,b,c
  float a, b, c;
  a = 3.0;
  b = 4.0;
  c = 6.0;
 
  // 辺の長さがa,b,cとなる三角形が存在するか
  if( ( a < b+c ) && ( b < c+a ) && ( c < a+b ) ){
    println("三角形が存在する");  
    drawTriangle(a,b,c); // 三角形を描く
  } else {
    println("三角形が存在しない");
  }
}

// 三角形を描く関数
void drawTriangle(
  float a,
  float b,
  float c
){

  // cの長さがキャンバスの幅の3/5になるように辺の長さを調整する
  float a2, b2, c2;
  c2 = width * 3.0 / 5.0 ;
  a2 = a * c2 / c;
  b2 = b * c2 / c;
  
  // 三角形の頂点の座標
  float A_x, A_y, B_x, B_y, C_x, C_y;
  A_x = 0.0;
  A_y = 0.0;
  B_x = c2;
  B_y = 0.0;
  C_x = (c2*c2 + b2*b2 - a2*a2) / 2.0 / c2;
  C_y = sqrt( (a2+b2+c2) * (-a2+b2+c2) * (a2-b2+c2) * (a2+b2-c2) ) / 2.0 / c2;

  // 三角形を描く
  triangle(A_x, A_y, B_x, B_y, C_x, C_y);
}

ソースコード2　存在する場合三角形を描くプログラム

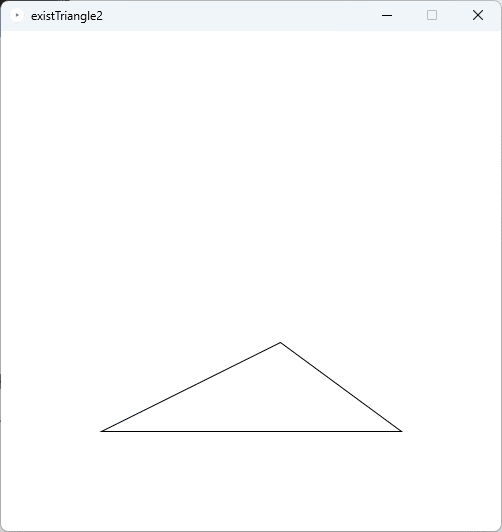
ソースコード2を、Processingの開発環境ウィンドウを開いて（スケッチ名を「existTriangle2」としています）、テキストエディタ部分に書いて実行すると、三角形の存在の判定結果がコンソールに出力されるとともに、実行ウィンドウのキャンバスにその三角形が描かれます。

プログラムの解説1「三角形を描く関数」

ソースコード2を見てもらうとわかるように、三角形を描く部分は関数（関数名を「drawTriangle」としています）にしました。引数は三角形の３辺の長さ$${a,b,c}$$としています。そして、この三角形を描く関数 drawTriangle を三角形が存在すると判定された場合の処理として呼び出しています。

  // 辺の長さがa,b,cとなる三角形が存在するか
  if( ( a < b+c ) && ( b < c+a ) && ( c < a+b ) ){
    println("三角形が存在する");  
    drawTriangle(a,b,c); // 三角形を描く
  } else {
    println("三角形が存在しない");
  }

この drawTriangle 関数の処理は、上記『三角形を描く方法』で紹介したように、三角形の３辺の長さ$${a,b,c}$$から、三角形の３つの頂点の座標を指定及び算出して、triangle 関数を用いて三角形を描きます。
ただ、与えられた３辺の長さ$${a,b,c}$$をそのまま利用すると、三角形をうまく描けない可能性があります。実際、ソースコード2では、

// 三角形の3つの辺の長さa,b,c
float a, b, c;
a = 3.0;
b = 4.0;
c = 6.0;

と与えており、そのまま利用すると、非常に小さな三角形を描くことになります。
そこで、三角形を描く関数内部で、３辺の長さの比$${a:b:c}$$を保持したまま三角形の大きさを調整するようにしました。具体的には、$${c}$$の大きさがキャンバスの幅の5分の3の長さになるように調整し、それに合わせて辺$${a,b}$$の長さを調整しています。

// cの長さがキャンバスの幅の3/5になるように辺の長さを調整する
float a2, b2, c2;
c2 = width * 3.0 / 5.0 ;
a2 = a * c2 / c;
b2 = b * c2 / c;

プログラムの解説2「座標系の位置」

もう一つ、座標系の位置について少し工夫をしています。
記事『高校数学をプログラミングで解く（数学A編）「2-3 三角形の五心」』などでは、座標系の原点がキャンバスの中央の位置に来るように調整していました。その結果、$${\triangle \mathrm{ABC}}$$の頂点$${\mathrm{A}}$$を座標系の原点に来るようにしていたので、三角形が全体的に右上に寄ってしまうような形になっていました。
今回は、三角形をできるだけ中央に描くように座標系の位置を調整しています。具体的には、座標系の原点の位置を、キャンバスの左上からキャンバスの幅の5分の1、キャンバスの高さの5分の4の位置に設定しています。

translate(width/5.0, height*4.0/5.0); // 座標の中心を移動する

つまり、実行ウィンドウのキャンバス上では、図6のような座標系が設定されています。

まとめ

今回は、数学Aで学ぶ「三角形の辺と角」における三角形の3辺の長さの性質を用いて、三角形の存在判定を行うプログラムを作成しました。
三角形の3辺の長さの性質は2つの表現があり、今回は「和」の方を利用しましたが、もちろん「差」の方を利用してもプログラムを作ることができます。演習問題としたのでぜひプログラムを書いてみてください。
また、三角形が存在する場合はその三角形を描くようにしました。その際、三角形を描くための関数を準備してプログラムで利用しました。関数の作成はプログラムを書いていく上で重要な方法になります。ぜひこの関数化の方法にも少しずつ慣れていってください。

参考文献

改訂版教科書傍用スタンダード数学A（数研出版、ISBN9784410209277）

演習問題

今回の問題を三角形の3辺の長さの性質②を用いて三角形の存在判定を行って、その結果をコンソールに出力し、また存在する場合はその三角形を描くプログラムを作成してください。

演習問題の解答例

ここから先は

689字 / 2画像 / 1ファイル

期間限定！Amazon Payで支払うと抽選で
Amazonギフトカード5,000円分が当たる

ログイン

この記事が気に入ったらチップで応援してみませんか？