
高校数学をプログラミングで解く(数学A編)「3-1 約数と倍数」
マガジンリスト > 数学A編 3.整数の性質 > 3-1 約数と倍数
はじめに
今回は、数学Aで学ぶ「約数と倍数」について、整数$${N}$$の約数を求めるプログラム、整数$${N}$$以下の素数を求めるプログラム、そして整数$${N}$$を素因数分解するプログラムを作成します。
整数Nの約数を求める
まず、整数$${N}$$の約数を求めるプログラムを作成します。
整数Nの約数の求め方
整数$${N}$$の約数を求める方法として一番素朴な方法は整数$${N}$$以下の自然数すべてについて、順に整数$${N}$$を割ったときに、
・割り切れれば(つまり余りが$${0}$$になれば)その自然数は整数$${N}$$の約数
・割り切れなければ約数ではない
と判定していく、という方法が考えられます。今回はこの素朴な方法で整数$${N}$$の約数を求めるプログラムを作成します。
整数Nの約数を求めるプログラム
今回は$${N=36}$$に対してその約数を求め、コンソールに出力するプログラムを作りました。
// 整数Nの約数を求める
void setup(){
// 整数N
int N;
N = 36;
// 整数Nが整数nで割り切れたらiはNの約数
for(int n=1; n<=N; n++){
if( N%n == 0 ){
println(n);
}
}
}ソースコード1 整数$${N}$$の約数を求めるプログラム
このソースコードを、Processingの開発環境ウィンドウを開いて(スケッチ名を「getDivisor」としています)、テキストエディタ部分に書いて実行すると、図1のように、コンソールに小さい方から順番に約数を出力します。

整数$${N}$$の値を変えてみて、正しい約数が出力されるか試してみてください。
整数N以下の素数を求める
次に、素数を求めるプログラムを作成します。ただし、素数は無限にありますので、整数$${N}$$以下の素数に絞って考えます。
整数N以下の素数の求め方
素数について復習しておきましょう。
素数
$${2}$$以上の自然数で、$${1}$$とそれ自身以外に正の約数をもたない数
この素数の定義から、ある整数$${n}$$が素数であるかどうかは、整数$${n}$$を$${2}$$以上$${n}$$未満のすべての自然数で順番に割ったときにいずれの自然数でも割り切れなければ、$${n}$$は素数であることがわかります。
整数N以下の素数を求めるプログラム
このことを用いて、整数$${N}$$以下の素数を求めるプログラムを書くことができます。今回は$${N=20}$$としています。
// 整数N以下の素数を求める
void setup(){
// 整数N(ただし、Nは2以上)
int N;
N = 20;
println(2); // 最初の素数をコンソールに出力
boolean pn_flag; // 素数かどうかのフラグ
// 3以上N以下の整数について素数であるかを確認する
for(int n=3; n<=N; n++){
pn_flag = true;
for(int m=2; m<n; m++){
if( n%m == 0 ){ // mで割り切れたらnは素数でない
pn_flag = false;
}
}
if(pn_flag){
println(n);
}
}
}
ソースコード2 整数$${N}$$以下の素数を求めるプログラム
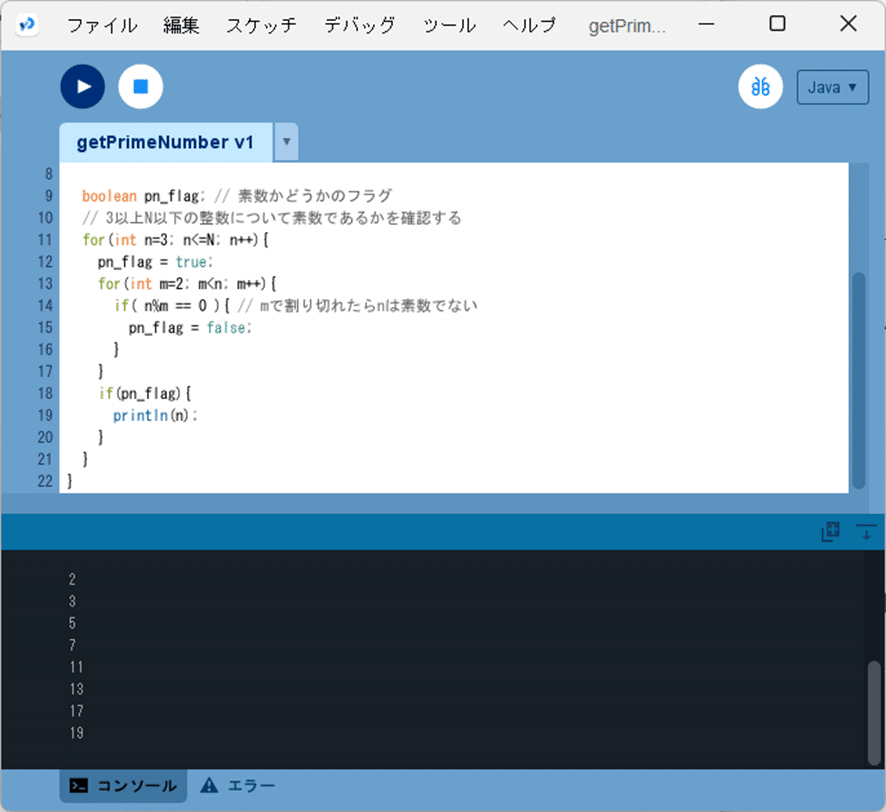
ソースコード2を、Processingの開発環境ウィンドウを開いて(スケッチ名を「getPrimeNumber_v1」としています)、テキストエディタ部分に書いて実行すると、図2のように、コンソールに小さい方から順番に$${N}$$以下の素数を出力します。
プログラムの解説1「素数「2」の扱い」
最初の素数である「2」は特に判定は行わずにそのまま素数としてコンソールに出力するようにしています。
プログラムの解説2「boolean型変数の利用」
今回、素数かどうかを判定するフラグ(ソースコード 2の変数「pn_flag」)として、boolean型変数を導入しています(boolean型変数については、記事『高校数学をプログラミングで解く(準備編)「1-3 データ型、変数、コメント、コンソール出力」』で説明しています)。boolean型変数は、2つの値「true」と「false」をとります。つまり、正しい(真)か、正しくない(偽)かの2つの値をとります。今回のケースでは、素数であれば pn_flag を true、素数でなければ pn_flag を false にします。
プログラム(ソースコード 2)では、はじめに pn_flag を true に設定しておき、整数$${n}$$が$${3}$$以上$${n}$$未満の整数のいずれかで割り切れれば$${n}$$は素数ではないので pn_flag を false に変更するようにし、いずれでも割り切れなけば何もしない(つまり、pn_flag を true のまま)ようにしています。そして、この判定が終わった後に、pn_flag が true であれば、$${n}$$の値をコンソールに出力し、pn_flag が false であれば何もしないことにしています。
整数N以下の素数を求めるプログラムを改良する
ソースコード2で整数$${N}$$以下の素数を求めるプログラムを作成しましたが、多少処理に冗長な部分があります。この冗長部分について解説したあと、プログラムを改良します。
素数であるかのチェックは奇数のみで十分
$${2}$$以外の偶数は素数ではないので、整数$${N}$$以下の自然数すべてに対して素数であるかをチェックする必要はなく、$${3}$$以上$${N}$$以下の奇数に対してのみチェックすればよいことになります。また、$${m}$$の値についても$${2}$$以上$${n}$$未満の整数ではなく、$${3}$$以上$${n}$$未満の奇数でよいことがわかります。
これを実現するために、forループを少し工夫します。つまり、
for(int n=3; n<=N; n++){ではなく(これでは3以上$${N}$$以下の整数となる)、
for(int n=3; n<=N; n+=2){とすることで、$${3}$$以上$${N}$$以下の奇数のみとなります。
素数でないと判定されたら処理を終了する
整数$${n}$$が$${3}$$以上$${n}$$未満の奇数$${m}$$で割り切れるかを順に確認していますが、まだ冗長部分があります。たとえば$${n=15}$$の場合、$${m=3,5}$$で割り切れるので$${m}$$の値がこれら2つのときに pn_flag が false に変更されますが、この変更は最初の$${m=3}$$のときのみ実行すればよく、$${m=5}$$のときは変更する必要がありません。そのため、pn_flag が false に変更されたら、以後の$${m}$$の値での処理は必要なくなります。
これを実現するために、if文の処理に「break」を挿入します。つまり、
for(int m=3; m<n; m+=2){
if( n%m == 0 ){ // mで割り切れたらnは素数でない
pn_flag = false;
}
}のif文の中に
for(int m=3; m<n; m+=2){
if( n%m == 0 ){ // mで割り切れたらnは素数でない
pn_flag = false;
break;
}
}と「break;」を入れます。これにより、if文の条件を満たし処理が実行されると、それ以後のforループの処理は実行せずループを抜けて、次の処理へ移ります。
改良したプログラム
これらのことを用いて、整数$${N}$$以下の素数を求めるプログラムを改良します。
// 整数N以下の素数を求める
void setup(){
// 整数N(ただし、Nは2以上)
int N;
N = 20;
println(2); // 最初の素数をコンソールに出力
boolean pn_flag; // 素数かどうかのフラグ
// 3以上N以下の整数について素数であるかを確認する
for(int n=3; n<=N; n+=2){
pn_flag = true;
for(int m=3; m<n; m+=2){
if( n%m == 0 ){ // mで割り切れたらnは素数でない
pn_flag = false;
break;
}
}
if(pn_flag){ // nが素数と判定されたらコンソールに出力
println(n);
}
}
}ソースコード3 整数$${N}$$以下の素数を求めるプログラムの改良
ソースコード3を、Processingの開発環境ウィンドウを開いて(スケッチ名を「getPrimeNumber_v2」としています)、テキストエディタ部分に書いて実行すると、図3のように、コンソールに小さい方から順番に$${N}$$以下の素数を出力します。ソースコード2と同じ結果です。

整数N以下の素数を保存する
次に解説する整数$${N}$$の素因数分解では、整数$${N}$$以下の素数を事前に求めてそれらの素数を利用して素因数分解を行います。そのため、整数$${N}$$以下の素数を配列に保存するようにプログラムを改良しておきます。
可変配列を利用する
整数$${N}$$以下の素数を配列に保存していくわけですが、整数$${N}$$以下の素数の個数を事前に求めることは行わずに保存できるように、可変配列を利用します。Processing(プログラミング言語Java)では、可変配列としてArrayListクラスを利用することができます(ArrayListに関する詳細は記事『高校数学をプログラミングで解く(準備編)「2-4 配列」』で説明していますので、そちらをご覧ください)。
また、可変配列を利用することで、素数$${n}$$が素数であるかの判定をもう少し簡略化できます。素数$${n}$$が素数であるかを確かめるために$${3}$$以上$${n}$$未満のすべての奇数で割り算を行う必要はありません。たとえば、ある整数が素数$${3}$$で割り切れない場合、$${3}$$の倍数である$${9}$$でも割り切れません。つまり、ある整数$${n}$$が素数であるかどうかは、整数$${n}$$を$${3}$$以上$${n}$$未満のすべての奇数で順番に割る必要はなく、$${3}$$以上$${n}$$未満のすべての素数で順番に割っていくことで判別することができます。「$${3}$$以上$${n}$$未満のすべての素数で順番に割っていく」を行うためには「$${3}$$以上$${n}$$未満のすべての素数」を事前に求めておく必要がありますが、これは整数$${n-1}$$までの素数を可変配列に格納しておいて整数$${n}$$の素数判定に利用することで実現することができます。
整数N以下の素数を可変配列に保存するプログラム
以上のことを踏まえて、整数$${N}$$以下の素数を求めて可変配列に保存するプログラムを作成します。
// 整数N以下の素数を求める
void setup(){
// 整数N(ただし、Nは2以上)
int N;
N = 20;
// 素数を格納するため、int型の可変配列を準備する
ArrayList<Integer> prime_numbers = new ArrayList<Integer>();
// 最初の素数2を可変配列に追加
prime_numbers.add(2);
println(prime_numbers.get(0));
int pn; // 素数を代入する変数
boolean pn_flag; // 素数かどうかのフラグ
// 3以上N以下の奇数について素数であるかを確認する
for(int n=3; n<=N; n+=2){
pn_flag = true;
for(int j=1; j<prime_numbers.size(); j++){ // n-1以下の素数を利用
pn = prime_numbers.get(j); // j番目の素数を取り出す
if( n%pn == 0 ){ // n未満の素数で割り切れたらnは素数でない
pn_flag = false;
break;
}
}
if(pn_flag){ // nが素数と判定されたらコンソールに出力
prime_numbers.add(n); // nが素数と判定された場合、可変配列に追加
println(n);
}
}
}ソースコード4 整数N以下の素数を求めて可変配列に保存するプログラム
ソースコード4を、Processingの開発環境ウィンドウを開いて(スケッチ名を「getPrimeNumber_v3」としています)、テキストエディタ部分に書いて実行すると、図4のように、コンソールに小さい方から順番に$${N}$$以下の素数を出力します。ソースコード2やソースコード3と同じ結果です。

整数Nを素因数分解する
最後に、整数$${N}$$を素因数分解するプログラムを作成します。
整数Nの素因数分解のやり方
素因数分解について復習しておきます。
素因数分解
自然数を素数だけの積の形に表すこと
したがって、ある自然数$${N}$$を素因数分解する場合、まず$${N}$$以下の素数を求めておいて、以下の手順で$${N}$$を素数で分解していけばよいです。
①割り算の商を表す変数$${q}$$を準備し、$${q}$$に$${N}$$を代入して初期化しておく。
②$${N}$$以下の素数から一つの素数$${n}$$を取り出し、$${q}$$を$${n}$$で割る。
③$${q}$$が$${n}$$で割りきれる場合、$${n}$$を素因数として出力し、$${q}$$の値を$${q}$$を$${n}$$で割ったときの商で更新する。再度$${q}$$が$${n}$$で割りきれるかを確認し、割り切れなくなるまで、この処理を繰り返す。
④割り切れなくなった場合、$${N}$$以下の素数から次の素数$${n}$$を取り出し、再度③の処理を行う。これをすべての$${N}$$以下の素数に対して行う。
整数Nを素因数分解するプログラム
以上のことを踏まえて、整数$${N}$$を素因数分解するプログラムを作成します。今回は$${N=60}$$としています。
// 整数Nを素因数分解する
void setup(){
// 整数N(ただし、Nは2以上)
int N;
N = 60;
// int型の可変配列を準備する
ArrayList<Integer> prime_numbers = new ArrayList<Integer>();
// 最初の素数2を可変配列に追加
prime_numbers.add(2);
int pn; // 素数を代入する変数
boolean pn_flag; // 素数かどうかのフラグ
// 3以上N以下の奇数について素数であるかを確認する
for(int i=3; i<=N; i+=2){
pn_flag = true;
for(int j=0; j<prime_numbers.size(); j++){
pn = prime_numbers.get(j); // j番目の素数を取り出す
if( i%pn == 0 ){ // i未満の素数で割り切れたらiは素数でない
pn_flag = false;
break;
}
}
if(pn_flag){
prime_numbers.add(i); // iが素数と判定された場合、可変配列に追加
// println(i);
}
}
// 整数Nを素因数分解する
int quotient = N; // 素数で割ったときの商
boolean divisible_flag; // 割り切れたかどうかを判定するフラグ
for(int i=0; i<prime_numbers.size(); i++){
pn = prime_numbers.get(i); // i番目の素数を取り出す
divisible_flag = true;
while(divisible_flag){
if( quotient % pn == 0 ){ // 商が素数pnで割り切れた場合
println(pn);
quotient = quotient / pn; // 商を更新する
} else { // 素数pnがNの素因数ではない、またはpnがNの素因数としてすべて算出された場合
divisible_flag = false;
}
}
}
}
ソースコード5 整数$${N}$$を素因数分解するプログラム
ソースコード5を、Processingの開発環境ウィンドウを開いて(スケッチ名を「primefactorization」としています)、テキストエディタ部分に書いて実行すると、図5のように、コンソールに小さい方から順番に$${N}$$の素因数を出力します。

まとめ
今回は、数学Aで学ぶ「約数と倍数」について、整数$${N}$$の約数を求めるプログラム、整数$${N}$$以下の素数を求めるプログラム、そして整数$${N}$$を素因数分解するプログラムを作成しました。いずれのプログラムも処理としてはそんなに難しいことは行っていませんが、初学者には多少複雑なプログラムに見えるかもしれません。そのような方は、プログラムが正常に動いたら、$${N}$$の値を変えて結果を確認しつつ、ソースコードの一行ずつ見直して、その部分がどういう処理を行っているのかを考えてみることをお勧めします。
参考文献
改訂版 教科書傍用 スタンダード 数学A(数研出版、ISBN9784410209277)
演習問題
$${N=100}$$以下の双子素数の組を求めて、コンソールに出力するプログラムを作成してください。
なお、双子素数とは、その差が$${2}$$となる二つの素数の組を構成する各素数のことを言います。
演習問題の解答例
ここから先は
この記事が気に入ったらチップで応援してみませんか?
