ギャンブラー必読？条件付確率ってやつPart2

先週に引き続いて４枚ドアだった場合、５枚ドアだった場合を考える。

４枚ドアの場合
４枚のドアがあり、１枚を選び、その後、神様が外れのドアを一つ教えてくれる。残りの２枚に変えるか、そのまま最初に選んだドアのままにいるか。

果たして、この場合も変えた方が当たる確率が高いのか。計算上は、以下のようになり、確率は変更した方が高くなる。

と言いながら、当たる確率は3/8なので、当たる確率は低いのだが、2/12　=　1/6 よりは高い。

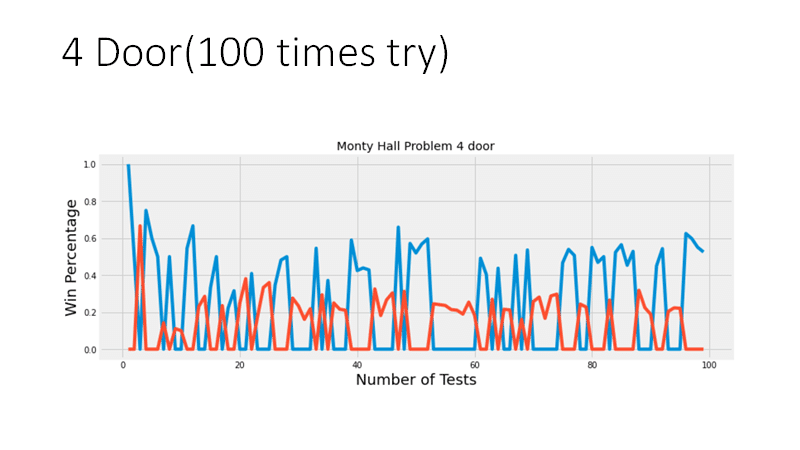
シミュレーションを流してみると以下のようになる。100回回してみた。
前回と同じく、青が変えた場合で、赤が変えなかった場合の勝つ確率。
確かに傾向としては、青が多いように見えるが、よくわからない。

そこで、今回も1,000回回してみると、クリアにわかる。青の方が確率が高い。４枚ドアでも選択したドアを変えた方が当たる確率が高い。

５枚ドアの場合

もう、同じだと思うが一応５枚ドアでも確認する。100回ではきっとわからないので、最初から1,000回で回してみる。

これも青（変更）の方が確率が高い。ただ、４枚ドアだと0.5ぐらいの確率を推移するが、5枚ドアだと0.4位を推移する。当たる確率自体はドアの枚数が多いほど当然下がるが、それでも変更しないよりは高い。

結果として、モンティホール問題で言われていることは正しく、ドアを変更した方が当たる確率が高いことが分かった。

未だに数学式では分からないが、ここまでのシミュレーションで、変えた方が良いんだなということが分かって自分としてはよかった！

今週はここまでです！