記事一覧
【複素解析】ゼータ正規化でsinが出るやつ
以前単純な場合でのゼータ正規化を求めた。
ここでは
$$
\prod_{n=-\infty}^{\infty} (n+a)=-2i\sin(\pi a)
$$
を求めていく。(参考文献:江口徹, 菅原裕二「共形場理論」)
ゼータ正規化ゼータ正規化は形式的には「総乗の中にゼータ関数を見出して置き換える」ことで行える。つまり
$$
\zeta(s)=\sum_{n=1}^{\infty} \
共形ゲージにおける2次元Ricciスカラー曲率
2次元の計量は共形ゲージで
$$
ds^{2}=-e^{2\omega(u,v)}dudv
$$
と書ける。このとき曲率は
$$
R=8e^{-2\omega}\partial_{u}\partial_{v}\omega
$$
となる。これは計量を
$$
g_{uu}=g_{vv}=0,\quad g_{uv}=g_{vu}=-\frac{1}{2}e^{2\omega}
$$
と置き
【複素解析】純虚数を引数に持つガンマ関数の2乗
有名なはずなのに意外とネット上では見なかったので(全然ありそう)。実数$${x}$$に対して
$$
|\Gamma (ix)|^{2}=\frac{\pi}{x \sinh{ \pi x}}
$$
のように双曲線関数が出るというもの。
使うもの相反公式
$$
\Gamma(z)\Gamma(1-z)=\frac{\pi }{\sin{\pi z}},\quad z\in \mathbb{C
【一般相対論】ブラックホールに自由落下するのにかかる時間
外から見るとブラックホールに落ちる人は無限の時間をかけて落下していくのに対して、落ちている本人からすれば普通に落下していく(局所的に平坦である)ので有限の時間で落ちる。という計算。ここで考えるブラックホールはSchwarzschildブラックホールである。
はじめにゼミ中で手間取ったので。SusskindのThe Holographic Universeにある
$$
\begin{align*
【ベクトル解析(?)】球座標のラプラシアンをうまく計算したい
この記事は一般相対論の知識がある人に向けて、球座標(3次元極座標)ラプラシアンの計算方法をメモしたものである。使うものはスカラー場の作用と最小作用の原理である。
球座標ラプラシアンの表示ラプラシアンはざっくりいえば偏微分のナブラ$${\nabla}$$を2回作用させる演算子である。直交座標系であれば$${\nabla=(\partial_{x},\partial_{y},\partial_{z}
【Fourier解析】デルタ関数を級数展開してみよう
この記事はDiracのデルタ関数を複素Fourier級数展開してみようというもの。意外とFourier変換に比べて出現頻度は低い……?と思ったときに限って出てくるので一応まとめておく(閉弦の扱いがさあ!一瞬迷ってさあ!)。
まず、複素Fourier級数展開は関数$${f(x)}$$が$${x\sim x+2\pi}$$で周期的としたとき
$$
f(x)=\sum_{n\in \mathbb{Z
Noteで数式を使う際のメモ
はじめに参考文献を挙げる(こっち読んだほうが早いので)
使えるのは基本的に$${\KaTeX}$$の記法であり、インライン表示・ディスプレイ表示に対応している。
インライン表示文中に数式を挿入する。ドルマーク$を2つと波カッコ{}で囲む。通常のLaTeXのインライン数式と同じ感じで出る。編集中のプレビューも出る。
(入力)
1次関数$${y=ax}$$を考える。ただし$${a>0}$$であ
【複素解析】自然数を全部かけたら√2π??
こんな公式がある。
$$
1\times 2\times 3\times \cdots = \sqrt{2\pi}
$$
は?
$$
\prod_{n=1}^{\infty} \frac{c}{n}=\sqrt{\frac{1}{2\pi c}}
$$
えぇ……
これらは$${\zeta}$$関数正規化を行うことで正当化される。もちろん、通常の意味では当然発散するし、意味のない式である。
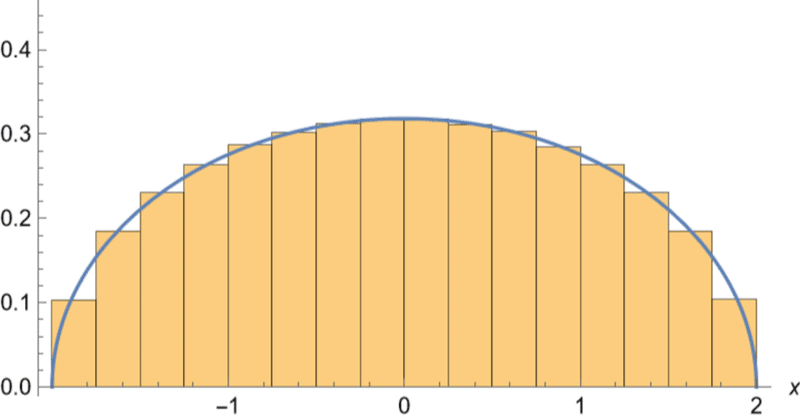
【ランダム行列】MathematicaでWigner半円則を見てみよう
タイトルの通り、この記事ではMathematicaを用いてWigner半円則を見る。ただ確認にすぎないが、意外と日本語の情報が少ないので記した。同様の話題で書かれた記事もすでにあるにはあったが、それは本来Wigner半円則と呼ばれるものではなかったというか、私がほしかった情報ではなかったので、改めて本稿で紹介したいと思う。
Wigner半円則これはランダム行列の理論で、ポテンシャルをGauss型
【場の理論】生成汎関数の指数の肩には連結グラフのみが現れる
修論書いてたら自由エネルギーが連結グラフの和で表されるのってなんでだっけ、となってしまったのでメモ。坂本場の量子論(II)を参考にしたのでここよりそっち見たほうが早い。
導出導きたい式
$$
\displaystyle \frac{Z[J]}{Z[0]} =\exp\left( \sum_{j=1}^{\infty} \frac{1}{S_{j}}\mathcal{C}_{j}\right
【微分幾何】多脚場を用いたときの測度との関係について
やること題名のつけかたに迷ったが、導きたい式は以下である。
$$
e^{1}\wedge e^{2} =\sqrt{g}d^{2}x
$$
簡単のため2次元で行っている。
ここで正規直交な1形式を$${e^{a}=e^{a}_{b}dx^{b}}$$と2脚場で表し、計量はEuclid化されているとする。つまり$${ \eta_{\mu\nu}=\delta_{\mu\nu} }$$である。なお
【LaTeX】pLaTeX2eが必要というエラー
概要おそらくLaTeXを使う人間なら誰でも一度は見たであろうエラーメッセージである。
今回私が陥ったエラーは「他のフォルダでコンパイルできたファイルを、そのままコピーして別のフォルダに移しただけなのにコンパイルできなくなった」というもの。
原因はlatexmkrcファイルを移し忘れていたこと、そしてフォルダのパスに漢字が含まれていたことであった。フォルダ名を半角英数字にしたところビルドが通った。