
【夏休み企画】あまり触れない数学史、味わってみませんか?
みなさんこんにちは! LITの数学担当、Taroです!今回は夏休み企画第12弾「あまり触れない数学史、味わってみませんか?」と銘打って、学校の勉強ではあまり触れられることがない、数学者という変人(誉め言葉)たちの足跡をご紹介したいと思います。
もし、前回の記事をご覧になってなられていない方は、こちらからお読みください!
また、夏休み企画最初から読みたいよという方は、こちらからお読みください!
それでは早速、やっていきましょう~!
1.ヨーロッパの数学を復活させた数学者、フィボナッチ
まず、なぜヨーロッパで数学の火か消えることになってしまったのかについて、概要を軽くお話しします。
古代エジプトから伝わったヨーロッパにおける数学は、発展を遂げていました。あるとき、当時世界文化の中心であったアレクサンドリア(エジプト北部)で消えることになってしまいました。それは、ヒュパティアというギリシア系の数学者、天文学者、哲学者が大きく関わっています。
1-1.その日、ヨーロッパの火が消えた。
ヒュパティアは、哲学や、数学、天文学の修行をしながら、人にそれらを教えていました。当時のアレクサンドリアでは、キリスト教の人達が勢力を強めていました。さらに、エジプトを治めていた東ローマ帝国の皇帝テオドシウス1世が非キリスト教の宗教施設や神殿を破壊することを良しとしてしまったことで、あらゆる知識の集積庫であったアレクサンドリア図書館が破壊されてしまいました。
当然、そんなことが起きている中、神秘主義を考えない哲学を教えていたり、宗教を「迷信だ」と言い放っていたヒュパティアは狙われてしまいます。415年、ヒュパティアは、キリスト教徒により惨殺されてしまいました。
この事件を契機にアレクサンドリアから多くの優秀な学者たちが去ることになり、その後700年もの間、ヨーロッパにおける数学の火が消えてしまうことになったのでした。
1-2.ヨーロッパの火が再び灯る。
イタリアのピサ(ピサの斜塔で有名ですね)で、一人の数学者が産声を上げました。その数学者こそが、フィボナッチです。
フィボナッチは、商人の父と共に商取引のため北アフリカに移住しました。そして、北アフリカでアラビア数字(インドで発達した表記ではありますが)を学び、当時ヨーロッパで使われていたローマ数字より便利であることを学びました。

その後、エジプトなどを巡りつつ数学を学んだフィボナッチは、イタリアにもどり、1202年に『算盤の書』を出版しました。これが彼の功績といえるでしょう。
フィボナッチといえば、「フィボナッチ数列」が有名でしょう。フィボナッチ数列は『算盤の書』の内容の1つで、自然現象と大きく関わる不思議な数列です。詳しい内容は、夏休み企画後の記事でフィボナッチ数列について解説するつもりです。お楽しみに!
『算盤の書』は、ヨーロッパ全体に受け入れられ、商人の簿記や、利子計算などに役立てられました。ここから再び、ヨーロッパの数学の火は灯ることになります。
2.すべては手紙から始まった。パスカルとフェルマー
みなさんは、日常の中で様々な「確率」を考えることがありますか?例えば、明日の雨が降るかどうかの「降水確率」、はたまたゲームのガチャで望み通りのものが引ける「確率」などです。
このように、私たちの日常にはいたるところに「確率」が使われています。そんな「確率」がどのようにして生まれたのか。それには、パスカルとフェルマーという数学者がかかわってきます。
2-1.パスカルとフェルマー、それぞれの功績
まずは、この2人がどういったものを残したのかを説明します。
パスカルは10歳で、最古の数学者であるターレスが導いた「三角形の内角の和が180°である」ことを証明した、「神童」でした。
少し脱線しますが、ガウスという、人類最高の数学者と呼ばれていた人も、小学生でこれを証明しています。彼は2歳のころにはすでに計算ができていて、どんな数学の本もすぐに読んで理解してしまうような子供でした。世の中にはすごい人がたくさんいますね。
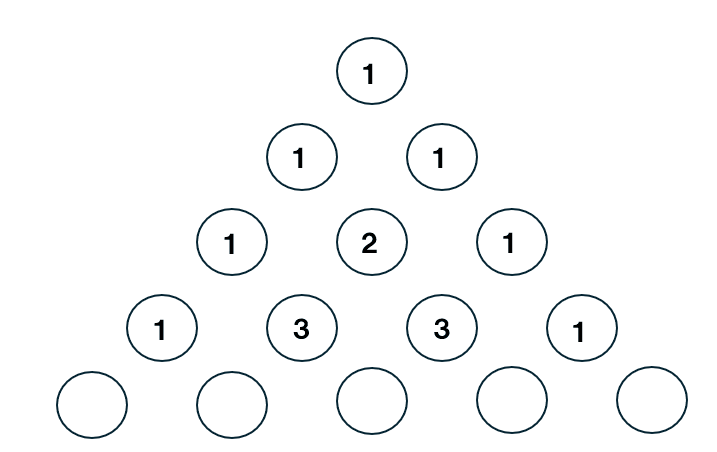
パスカルの有名な言葉に、「人間は考える葦である」という言葉があることから、パスカルは哲学者と思われがちですが、数学者でもあります。また、等比数列の和や、パスカルの三角形などを発見しました。(詳しくは調べてみてください!)
フェルマーは、主に確率論の構築、微分の微分係数、そして、彼の代名詞ともいえる数論に大きく貢献した数学者です。数論とは、私たちが使う数の性質を扱う分野であり、身近な例でいうと中学、高校の整数の性質などがこの分野の内容になります。(筆者はあまり得意ではありませんw)
フェルマーといえば「フェルマーの最終定理」が有名ですが、この問題が、後世の多くの数学者の人生を狂わせることになりますが、当の本人は「この本の余白は、証明を書くには狭すぎる」と言っていますw

実はフェルマーは大の証明嫌いでした。彼は完璧な証明に時間がとられるくらいなら、他の定理を見つけたほうがいいという考えでした。それだけなら良かったのですが、彼は「この定理を証明しろ」と挑戦状をたたきつけるような人だったので、他の数学者に好かれていなかったそうな(笑)
2-2.パスカルとフェルマー、確率論のはしり
ある日、パスカルのもとに友達から手紙が届きました。それは、ギャンブルの取り分の内容でした。皆さんも考えてみましょう。

この解に苦しんだパスカルは、フェルマーと共に、LさんとRさんの勝率を五分としました。これが、確率論の始まりとなっていきました。ちなみに、実際これがどうなったのかをいうと、「L:R=3:1」という結果になります。
なぜかを説明したいと思います。

上記のような考え方の図を「樹形図」といいます。現時点で、Lさんが2勝、Rさんが1勝しているので、ここから、1試合が終わるとその時点で勝負が決まるパターン(Lが勝つ)、お互いそれぞれに王手をかけるパターン(2対2)の2つに分かれます。さらにそこから1試合が終わると、勝敗が確定します。
確率を考えると、Lさんが勝つ確率が3/4、Rさんが勝つ確率は1/4となります。よって、勝つ確率の割合は(Lさん):(Rさん)=3:1となります。だから、パスカルとフェルマーは取り分を3:1としたんですね。
このように、確率論はギャンブルから始まりました。ギャンブルとだけ聞くと聞こえは悪いですが、確率をうまく考えることで、自分が今後どうするべきか決断を迫られたとき、助けてくれるツールとなります。現代では、確率はさまざまな事に使われています。ぜひ、この夏休みを使って調べてみてください!
3.まとめ
今回は、数学史についてお話しさせていただきました。偉大な変人たちがどのような人だったのか、どのような事を考えたのかをたどることも、普段の数学とは違って面白いものだと思います。
冒頭でもお話ししましたが、数学史自体は学校の勉強ではほとんど触れることがありません。ですが、こうした学校がない夏休みだからこそ、ぜひ数学史に触れてほしいと思っています。
数学は、過去の偉人たちが紡いできた1つの糸です。この糸を編むことで、理科という科目を筆頭に様々なものが発展していきました。この糸を、ゆっくりと眺めて、あわよくば美しいと思っていただければ幸いです。
ここまでお読みくださり、ありがとうございました!
夏休み企画は以上となりますが、今後も勉強に関する様々なトピックについて記事を投稿していきますので、ぜひ今後もお楽しみに!
お問い合わせ先
記事のご感想については、各記事のコメント欄にご記入ください。
また団体に関するご質問やご相談については下記のメールアドレスからご連絡いただけると幸いです。
メールアドレス
lightupyourtorch@gmail.com
