
31.01 ベクトルの初歩(幾何ベクトル)
「ベクトル」は、理科(物理)の「力」の表記や「力の合成と分解」だけでなく、日常においても「物事や考え方の方向」の意味で使われているので、耳にしたことがあると思います。
このシリーズは、主に高校数学「平面・空間のベクトル」の話をします。
①幾何ベクトル ②数ベクトル ③図形への応用 ④大学数学の入口
を予定しています。
ベクトルは数学者のハミルトン (W.R.Hamilton) (※1)が、ギリシャ語をもとに名付けたもののようです ([飯高])。英語で vector と書くので「ヴェクター」が英語の音に近いと思いますが、慣習に従いベクトルと表記します。
ベクトルは、物理学では、矢印 → で「力のはたらいている向き」、矢印の長さで「力の大きさ」を表します。ここでは幾何学的にベクトルを導入しますが、結果的に同じものです。
ベクトルは現代数学において欠かすことのできない概念で、あらゆるところに顔を出します。ここでは高校数学を主に扱うので、図形との絡みが多くなりますが、実際、図形を扱うときにとても便利な道具で、大学以降の数学(微分積分、ベクトル解析、微分幾何など)で再び登場します。ベクトルを抽象化したものはさらに多くの数学で用いられます。その抽象化されたベクトルは大学1, 2年の「線形代数」で学びます。
幾何ベクトル
平面または空間において、2点A, Bを直線で結んだものを線分といい、記号で AB または BA と書きました。この線分に向き (方向) を考慮し、$${\overrightarrow{\mathrm{AB}}}$$ と書いたらAからBへの向きの付いた有向線分を表すことにします。これによって、これまでは AB=BA でしたが、$${\overrightarrow{\mathrm{AB}}\neq\overrightarrow{\mathrm{BA}}}$$となります。
注意1:$${\overleftarrow{\mathrm{AB}}}$$という表記はしません。この記号での矢印は常に右向きです。
下図の平行四辺形ABCDにおいて
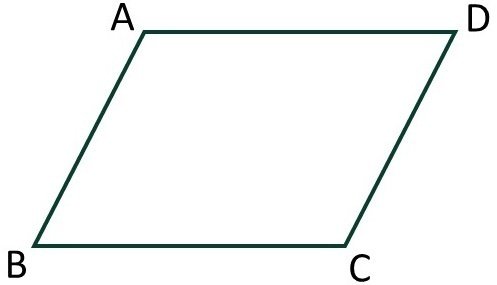
$${\overrightarrow{\mathrm{AD}}}$$と$${\overrightarrow{\mathrm{BC}}}$$は位置は異なりますが、向きと長さが等しい有向線分です。言い方を換えれば、平行移動させると2つの有向線分はぴったり重なります。
このような有向線分を同じものと見なしたものを幾何ベクトル (単に、ベクトル) と呼びます。つまり、位置は考えず、有向線分の向きと長さだけに着目したものが幾何ベクトル (ベクトル) です。今後は、単に、ベクトルと呼び、ベクトルを表すのに、有向線分と同じ表記を用いることにします。
ベクトル$${\overrightarrow{\mathrm{AB}}}$$と書いたら、向きと長さが等しい有向線分を代表していると読み取ります。
記号の読み方:ベクトルを表す記号$${\overrightarrow{\mathrm{AB}}}$$を、ふつう、ベクトルABと読みますが、ABベクトルと読んでも構いません。
注:ベクトル$${\overrightarrow{\mathrm{AB}}}$$と表記すると重複している感じを受けますが、これは有向線分$${\overrightarrow{\mathrm{AB}}}$$と区別するためであり、それぞれベクトルAB、有向線分ABと読みます。
安心して創作活動が続けられるよう応援してくださると助かります。いただいたチップは書籍もしくは文具の購入に当てたいと思います。

