
光とスクリーンが出たら算数だと思え!
問題
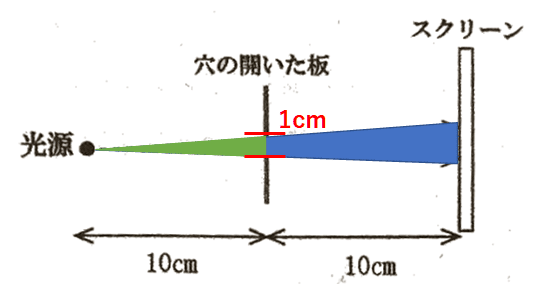
光源と、直径1cmの穴の開いた板、スクリーンを使って実験を行いました。はじめは下の図のように、光源と板の距離を10cm、板からスクリーンまでの距離を10cmにして、スクリーンに光を映しました。
問1 図の状態では、スクリーンに直径何cmの光が映りますか?
問2 スクリーンを右に20cm動かしました。スクリーンに映る光の円の直径は何cm?
問3 図の状態から、板を左に5cm動かしました。スクリーンの円は何cm?
問4 問2のとき、スクリーンに映った光の明るさは、最初の図のときと比べて何倍になりますか?

ここがだいじ
光の問題がきたら「算数」特に二等辺三角形の問題だと思って取り組もう!
この図を2つの二等辺三角形だとみなすと
このように「緑の三角形」と「青の三角形」になるね。
そしてこの2つの三角形は大きさは違うけど同じ形になる。

2つの三角形を立ててみた

問1は「?」を聞かれているね。
青の三角形の高さは緑の2倍になっている。
ということは青の底辺である「?」は緑の底辺1cmの2倍
よって2cm だ。
問2はスクリーンを右に20cm動かす。
すなわち青の三角形の高さが20cm高くなるということ。
なのでこんな図になるね。

あとは同じ考え方
青の三角形の高さは緑の4倍になっている。
ということは青の底辺である「?」は緑の底辺1cmの4倍
よって4cm だ。
問3 ポイントは板に直径1cmの穴が開いていること。
図にしてみよう。
最初はこうだね。
板を左に5cm動かすとこうなる。
三角形がぶっとくなるね。

後は同じ考え方。「緑の三角形」と「青の三角形」は二等辺三角形で同じ形。2つの三角形を立ててみた。

あとは同じ考え方
青の三角形の高さは緑の4倍になっている。
ということは青の底辺である「?」は緑の底辺1cmの4倍
よって4cm だ。
問4 最初の図のときと、問2のときの光の円の明るさを比べる問題。
穴の開いた板は動いていないので取り込む光の量は同じ。
同じ光の量だけど、表示する大きさが違うということ。
どっちが明るいかな?
最初の円の方が明るいね。
最初の図の光の円は 直径2cmの円 → 面積は? 3.14㎠だね
問2のときの光の円は 直径4cmの円 → 面積は? 12.56㎠だね
12.56 ÷ 3.14 = 4
よって問2のときの明るさは最初の明るさの 1/4倍になる。
※どれくらい暗くなるのか?と聞かれているので小さくなる。
ここがだいじ
・光は二等辺三角形の問題だと思って取り組む
・入ってくる光の量は同じ、それが分散されている。
・直径で比べるのではなく面積で比べる
