凸凹（でこぼこ）の平面図は無理やり外枠にあわせる

ポイント１
凸凹（でこぼこ）の面を底面にしよう
ポイント2
底面の外枠にあわせるため、無理やり辺を移動しよう

問題

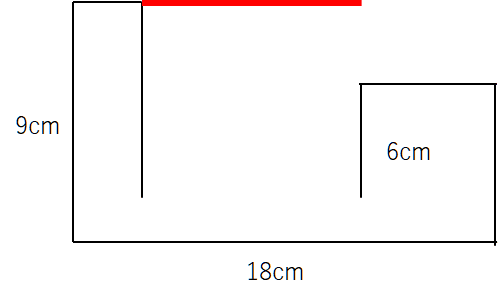
下の図のような、直方体から２つの直方体を切り取ったような立体があります。この立体の表面積が345㎠のとき、体積を求めなさい

立体を切って分けて、それぞれの立体の体積を出そうとするのが普通だと思う。でもね、この問題の場合はそれができないんだよ。
どこをどう切ってもうまくいかない。
こんな場合どうしたらよいのだろう。

まず、凸凹の面を底面にする。
体積＝底面積×高さ　だよね。
この場合、高さは？？

そう、4cm。
これはわかるよね。
だからこの立体の体積は
体積　=　底面積　×　4 cm
ということ

で、この立体の表面積を分解すると
表面積(345㎠)　＝　底面積×２　＋　側面積
になる。

やっつける相手が出てきたね。
そう、側面積だ。
これがわかればこの問題はやっつけることができる。

いまから教える事は他の立体でも、平面図でも使えるよ。
ポイントは辺を移動してしまうこと。

こう考えよう
面積の外枠にあわせる。そのため無理やり辺を移動しよう

外枠にあわせるってどういうことだろうか？
この図形の外枠とは縦9cm 横18cmの事

丁寧に説明するね。
まずはここの赤い線を見て。

赤い線を外枠に合わせるため、上に動かす。

するとこうなるね。

同じように、今度は青い線をみて。
これも移動しよう。
左と右、どっちに動かす？
そう右の外枠が空いてるよね。
だから右に動かすんだ。

そうするとこうなるね。

次は緑の線だ。

上に動かせば…

外枠の長方形が完成する
ちなみに、外枠の中にある縦線。
右側は6cm
左側は？　これも6ｃｍだね。

さて、ここで
さっき言ったことをもう一度。

体積　=　底面積　×　4 cm

表面積(345㎠)　＝　底面積×２　＋　側面積

側面積は、
底面積の各辺の長さ×高さ（４cm）になる
これはわかるよね。
だって、底面積の周りに立ってる壁
これが側面積だもの。

側面積の合計　＝　底面積の各辺の長さの合計　×　高さ（4cm）
になる。

そして
さっきまで移動していたのが、
底面積の各辺の長さの合計を出すためだ。

底面積の各辺の長さの合計は？

縦　9cm　が２つ
横　18cm　が２つ
中　6cm　が２つ

9 + 9 + 18 + 18 + 6 + 6 =  66

66cmだ。

ということは
この立体の側面積は　66 × 4(高さ) = 264㎠
この立体の表面積は　345㎠　（問題に書いてある）
ということは
この立体の底面積は　
（345 - 264 )　÷ 2 = 40.5 ㎠

てたね。
底面積は40.5 ㎠

体積　＝　底面積（40.5㎠）　×　高さ（4cm）なので

162㎤　になるね

今回のポイントは
底面積の外枠に合わせるため辺を移動したこと

似たような問題は結構でるので、
この考え方を是非マスターしよう！