
光の問題は算数で解く
問題
直径6cmのレンズを通った太陽光線は、下の図のように箱の中を進みました。箱の長さが18cmのとき、かべには3cm光の円がうつりました。
以下の問いに応えなさい。
問1 このレンズの焦点距離は何cmですか
問2 かべにうつった光の明るさは、太陽光線の何倍ですか。
問3 箱の長さをを6cm、8cm、24cmにしたときかべにうつる光の円の直径は何cmになりますか。それぞれについて答えなさい。

ここがだいじ
このような図が出てきたら、算数の問題だと思おう。
算数として考えれば難問ではないよ。
要素だけを抜き出してみる
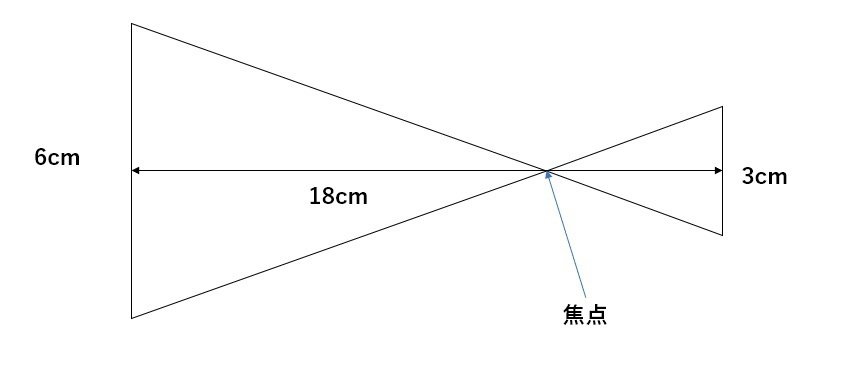
焦点を頂点にした大きい二等辺三角形と小さい二等辺三角形ができる。
大きい二等辺三角形の底辺は6cm
小さい二等辺三角形の底辺は3cm
とすると、
②:①の二等辺三角形になる
向きを変えてみよう。

底辺が6cmと3cmなので②:①の三角形。
だから高さも同じように②:①になる。
その高さ②と①をたすと
①+②=③
③=18cm
よって、①は3分の1なので6cm だね。
問1 聞かれているのは大きい二等辺三角形の高さのことなので②のこと
なので、答えは 12cm となる。
問2は見る角度を変えてみよう

左側からみると、このようになるね。

これは算数の円の面積と同じ考え方だね。
箱の手前側の円(レンズの事)の面積の分だけ光を獲得し
その光が箱の奥側に集まっていると考える。
箱の手前側の円の面積
3×3×3.14=28.26㎠
箱の奥側の円の面積
1.5×1.5×3.14=7.065㎠
28.26÷7.065= 4
よって4倍になる
問3 6cmの場合
緑の三角形にだけ注目するよ。焦点までの距離は12cmだったね。
この距離が半分の6cmになる。
すなわち高さが 12:6 = ②:①の二等辺三角形になるということ
であれば底辺も②:①
②が6cmなので、①は3cm
よって答えは 3cmだ。


問3 8cmの場合
同じ考え方だね。
緑の三角形の高さが12cm。
箱の長さが8cmの場合の三角形の高さは4cmになるね。
すなわり③:①の二等辺三角形
③=6cm なので ①=2cm
よって答えは2cmだ

正しくは③です
問3 24cmの場合
24cmということは最初の箱の長さ18cmより6cm長い。
焦点までの距離(=緑の三角形の高さ)は12cm
なので、24-12で、焦点からかべまでの距離も12cm
ということは全く同じ大きさの二等辺三角形になる。
よって、緑の三角形の底辺(=レンズ)6cmと同じ長さがかべにうつることになるね(青の三角形の底辺)

どうかな?
算数の二等辺三角形と比の問題だったよね。
しかも難易度は低めの問題だ。
理科だからといって、算数とは別ってことはないよ。
知っていることを使えばいいんだ。
自分の武器だからね。
