2006年 日本数学オリンピック本選　第１問 解答例

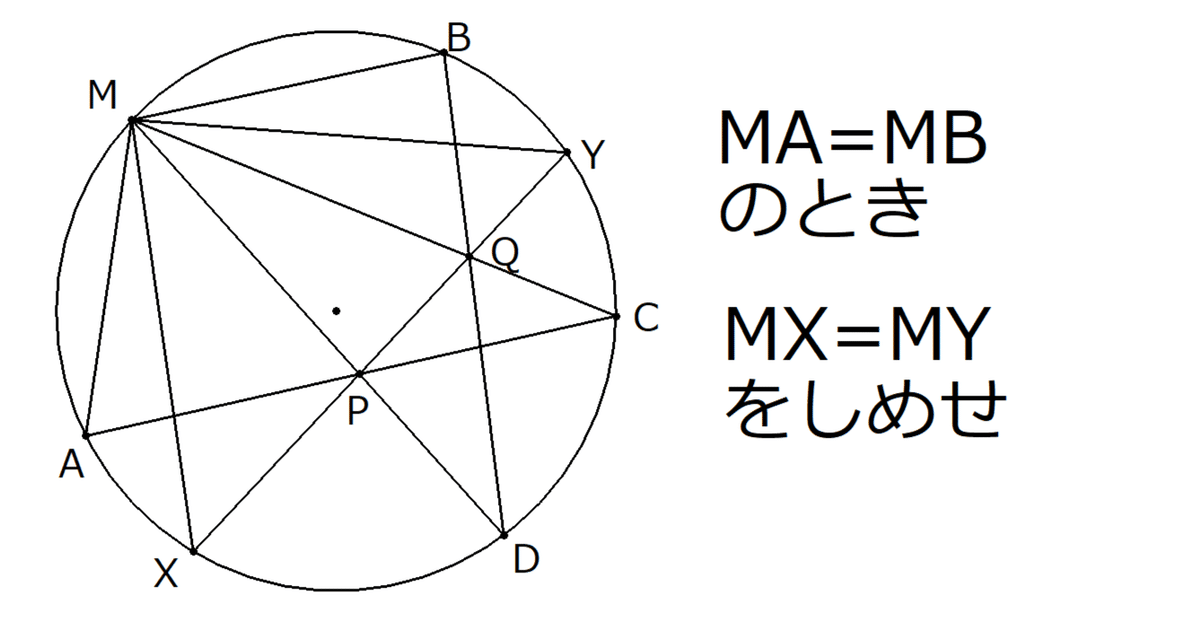
円$${O}$$の周上に相異なる５点$${A, M, B, C, D}$$がこの順に並んでおり、線分$${MA}$$と$${MB}$$の長さが等しいとする。直線$${AC}$$と$${MD}$$、直線$${BD}$$と$${MC}$$の交点をそれぞれ$${P, Q}$$とし、直線$${PQ}$$と円$${O}$$の周との２交点をそれぞれ$${X, Y}$$とするとき、線分$${MX}$$と$${MY}$$の長さが等しいことを示せ。

公益財団法人　数学オリンピック財団HP　  第16回(2006年)JMO本選の問題

考え方：

円に内接する四角形がたくさん出てきますが、
円$${O}$$とは違う円に内接する四角形があることに気づけるかどうかだけがポイントになります。

解答例：

同じ長さの弧に対する円周角なので$${\angle BDM = \angle MAC}$$であるから、
四角形$${PQCD}$$は円に内接する。
よって$${\angle QPC  = \angle QDC = \angle BAC}$$である。
つまり、$${AB}$$と$${XY}$$は平行である。
よって、円$${O}$$の中心を点$${O}$$とすると
$${X, Y}$$は直線$${MO}$$に対して対称であり*、
$${MX=MY}$$を得る。

補足：

*自明なのでこれでよいと思いますが、きちんと示すなら：
$${MO}$$と$${XY}$$は垂直なため、
$${MO}$$と$${XY}$$の交点を$${R}$$とすると
$${\triangle OXR \equiv \triangle OYR}$$ となり、
$${XR =YR}$$を得る。
よって、$${\triangle MXR \equiv \triangle MYR}$$より
$${MX=MY}$$となる。

お知らせ：

少しでも興味深い、楽しいと感じたらぜひスキやコメント、フォローください！
間違いなど見つけましたら是非お教えください。
他に公開している記事などの一覧はこちら
ぜひ初めに見てください。｜光捷 (note.com)