2018年 日本数学オリンピック本選 第2問 解答例
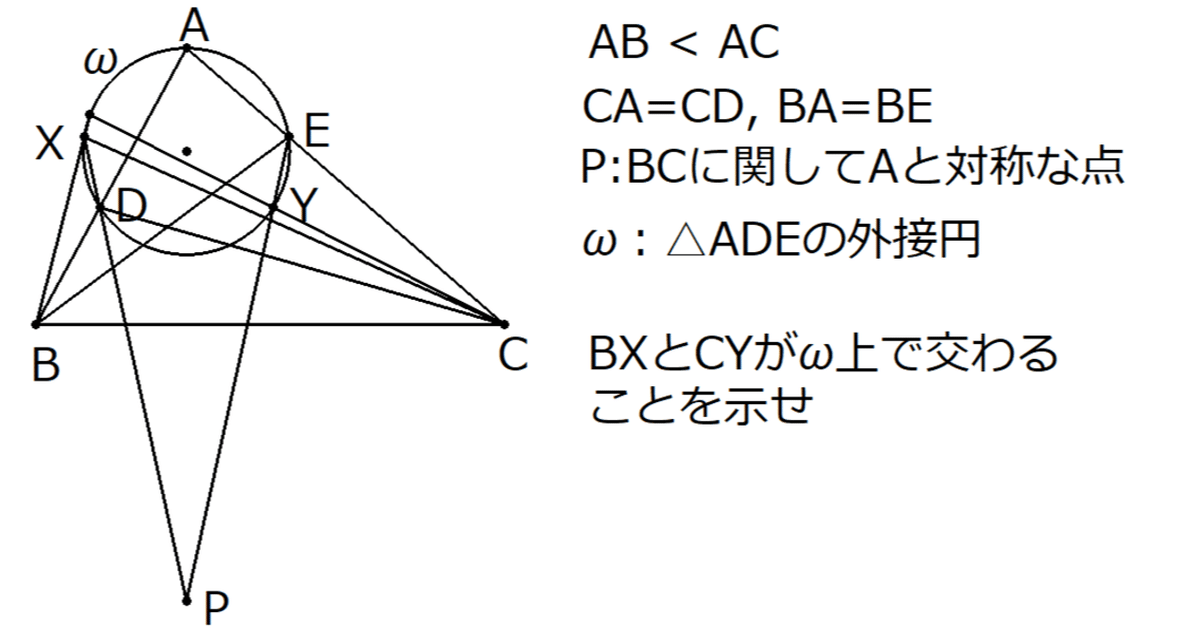
$${AB < AC}$$なる三角形$${ABC}$$の辺$${AB, AC}$$上(端点を含まない)に点$${D, E}$$があり、$${CA=CD, BA=BE}$$をみたしている。三角形$${ADE}$$の外接円を$${\omega}$$とし、さらに直線$${BC}$$に関して$${A}$$と対称な点を$${P}$$とおく。直線$${PD}$$と$${\omega}$$の交点のうち$${D}$$でない方を$${X}$$、直線$${PE}$$と$${\omega}$$の交点のうち$${E}$$でない方を$${Y}$$とするとき、直線$${BX}$$と直線$${CY}$$が$${\omega}$$上で交わることを示せ。
ただし、$${ST}$$で線分$${ST}$$の長さを表すものとする。
考え方:
角度を追って、同一円周上の点の組み合わせを探し、
さらに相似も駆使すれば初等幾何の知識で証明できるのですが、
なにせ登場する点が多いため線も多くなり複雑になっていきます。
新しいことが分かったときに、
逆に不要になった情報を消してシンプルな図を書き直して行った方が、
有効な補助線の引き方が見えやすいようです。
解答例:
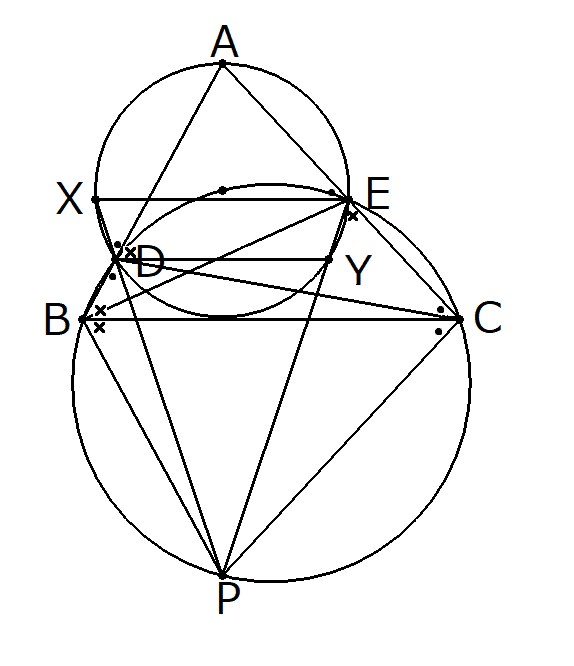
$${CA=CD, BA=BE}$$より$${\angle BEA = \angle BAC = \angle CDA}$$であるから、
$${\angle BEC = \angle BDC}$$である。
また、$${\angle BPC = \angle BAE = \angle BEA = 180^{\circ} - \angle BEC}$$である。
よって、$${B, D, E, C, P}$$は同一円周上にある。
そのため、$${\angle BCA = \angle BCP = \angle BDP = \angle XDA = \angle AEX}$$となるので、
$${XE}$$と$${BC}$$は平行である。
また、$${\angle CBA = \angle CBP = \angle CEP = \angle YDA}$$となるので、
$${DY}$$と$${BC}$$は平行である。

よって、$${DX = YE}$$であり、
同じ長さの弧に対する円周角なので$${\angle XAD = \angle YAE}$$が成り立つ。
これより、$${\angle XAY = \angle DAE}$$となる。
また、$${\angle XYA = \angle XEA = \angle BCA}$$であるから、
$${\triangle XYA}$$と$${\triangle BCA}$$は相似である。
よって、$${XA:AB = YA:AC}$$を得る。
そのため、$${\triangle XAB}$$と$${\triangle YAC}$$は相似であり、
$${\angle XBA = \angle YCA}$$となる。
$${BX}$$と$${CY}$$の交点を$${T}$$とする。
$$
\begin{align*}
\angle BTC &= 180^{\circ} - \angle TBC - \angle TCB\\
&= 180^{\circ} - \angle XBA - \angle ABC - \angle ACB + \angle YCA \\
&= 180^{\circ} - \angle ABC - \angle ACB\\
&= \angle BAC
\end{align*}
$$
となる。$${XY}$$は$${DE = XY}$$となる$${\omega}$$の弦であり、
$${\angle XTC = \angle BTC = \angle BAC}$$であるから、
$${T}$$は円$${\omega}$$上にある。
お知らせ:
少しでも興味深い、楽しいと感じたらぜひスキやコメント、フォローください!
間違いなど見つけましたら是非お教えください。
他に公開している記事などの一覧はこちら
ぜひ初めに見てください。|光捷 (note.com)
