2008年 日本数学オリンピック本選 第3問 解答例
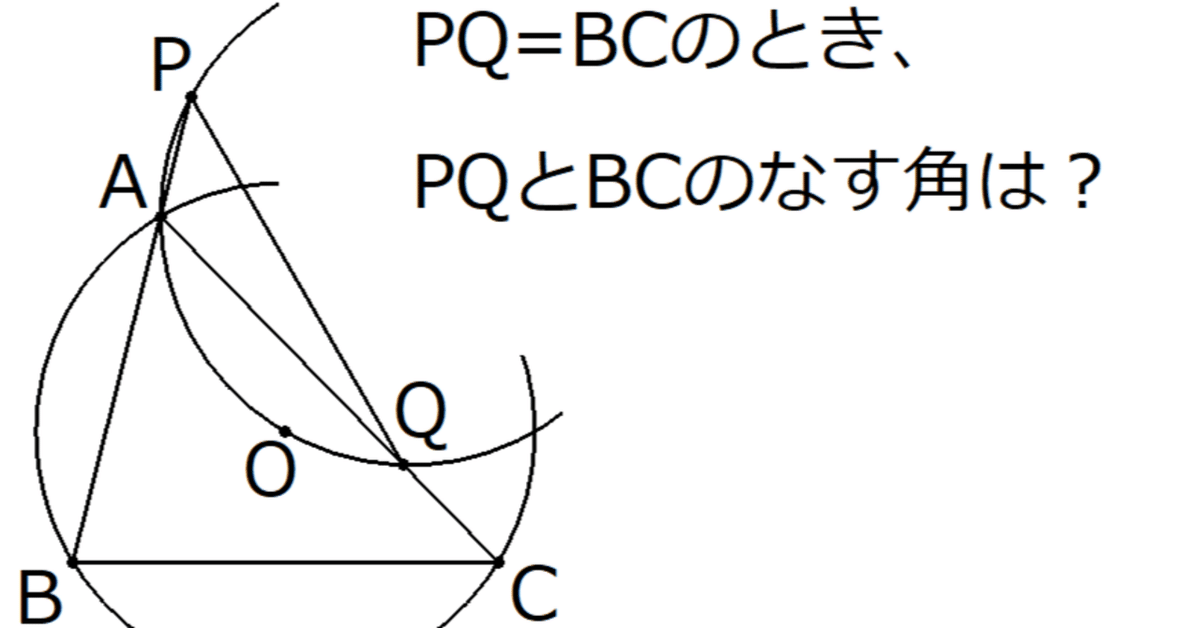
鋭角三角形$${ABC}$$の外心を$${O}$$とする。2点$${A, O}$$を通る円が、直線$${AB, AC}$$とそれぞれ$${A}$$以外の点$${P, Q}$$で交わっている。線分$${PQ}$$と線分$${BC}$$の長さが等しいとき、直線$${PQ}$$と直線$${BC}$$のなす角のうち$${90^{\circ}}$$以下の方の大きさを求めよ。
考え方:
第3問ということで身構えますが、1つ1つ角度を追っていけばそこまで難なくたどり着けます。
$${P, Q}$$と$${A}$$の位置関係がいくつか考えられますが、同様の考え方で処理できます。
向き付きの角度の概念を導入すれば、すべてのケースをまとめて処理できると思います。
解答例:

$${P, A, O, Q}$$を通る円の中心を$${O_2}$$とし、
直線$${OO_2}$$がこの円と交わる点であって$${O}$$でない点を$${R}$$とする。
まず$${B, A, P}$$の順に並んでいる時を考える。
$${Q}$$は$${A}$$から見て$${C}$$側に存在する。
$${\angle PRQ = 180^{\circ} - \angle PAC = \angle BAC}$$である。
また、$${PQ = BC}$$であることより、
同じ長さの弧に対する円周角が等しいことから、円$${ABC}$$と円$${PAOQ}$$の半径は等しい。
つまり、$${OA = O_2A = OO_2}$$であるから、
三角形$${OO_2A}$$は正三角形になる。
また、$${OR}$$は直径なので$${\angle OAR = 90^{\circ}}$$であるから、
直線$${RA}$$は円$${ABC}$$の接線である。
よって接弦定理より$${\angle RAC = \angle ABC}$$であり、
これと$${\angle QPR = \angle RAC}$$から$${\angle QPR = \angle ABC}$$である。
以上から、$${\angle PQR = \angle ACB}$$が得られる。
これと$${\angle POR = \angle PQR}$$から、$${\angle POR = \angle ACB}$$を得る。
$${PQ}$$と$${BC}$$のなす角度は、
$${\angle PQA + \angle ACB = \angle POA + \angle POR = 60^{\circ}}$$となる。
$${C, A, Q}$$の順に並んでいるときは$${B, C}$$および$${P, Q}$$を入れ替えて同じ議論をすればよい。
$${P}$$が$${A}$$から見て$${B}$$側にあり、$${Q}$$が$${A}$$から見て$${C}$$側にあるとき
$${O_2}$$が$${AO}$$より$${C}$$側にあるならば、
$${\angle BAC = \angle PRQ}$$が明らかであり、
以下同じ議論で$${\angle POR = \angle ACB}$$を得る。
$${PQ}$$と$${BC}$$のなす角度は、
$${\angle ACB - \angle AQP = \angle POR - \angle POA = 60^{\circ}}$$となる。
$${O_2}$$が$${AO}$$より$${B}$$側にあるならば、
$${B,C}$$および$${P,Q}$$を入れ替えて同じ議論をすればよい。
以上より、いずれの場合も求める角度は$${60^{\circ}}$$となる。
お知らせ:
少しでも興味深い、楽しいと感じたらぜひスキやコメント、フォローください!
間違いなど見つけましたら是非お教えください。
他に公開している記事などの一覧はこちら
ぜひ初めに見てください。|光捷 (note.com)
